ВСТУП

Для поняття "граф" немає загальновизнаного єдиного визначення. На математичній мові графом G (V, Е) прийнято називати сукупність непорожньої множини V елементів (вершин) і набору Е пар вершин (ребер). Нехай дана непорожня множина 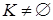 і на ній задані 2 алгебраїчні операції - додавання і множення. Нехай також виконуються наступні аксіоми:

а) ;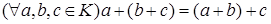

б) ;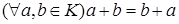

в) 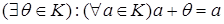. Елемент  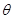називається нейтральним за додаванням (або нулем);

г) ;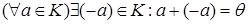

д) ;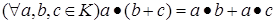

е) .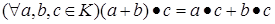

Тоді ця множина називається кільцем і позначається . Кільце називається асоціативним, якщо виконується така додаткова аксіома:

ж) .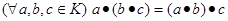

Якщо додатково виконується аксіома:

з) 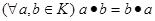, то кільце називається комутативним

Якщо в кільці :

и) 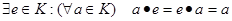, то елемент  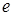називається нейтральним елементом по множенню (або одиницею кільця), а саме кільце називається кільцем з одиницею.

Якщо крім аксіом 1-8 виконується така умова:

к) 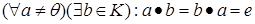, то кільце називають полем.

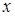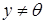Ненульовий елемент  кільця  називається лівим дільником нуля, якщо існує такий елемент , що 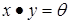. Аналогічно, ненульовий елемент кільця називається правим дільником нуля, якщо існує такий елемент 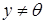, що 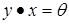. Елемент, який одночасно є і правим, і лівим дільником нуля, називається дільником нуля. Якщо множення в кільці комутативне, то поняття правого і лівого дільників нуля збігаються. Нуль називається невласним (тривіальним) дільником нуля. Відповідно, елементи, відмінні від нуля і є дільниками нуля, називаються власними (нетривіальними) дільниками нуля. Множину дільників нуля кільця  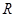прийнято позначати символом .

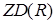У кваліфікаційній роботі розглядаються графи, вершинами яких є дільники нуля заданого скінченного кільця. Розглядаються необхідні для викладення матеріалу поняття: «кільце», «граф», «дільник нуля», «граф дільників нуля», «стиснений граф дільників нуля» будуються приклади графів дільників нуля для різних скінченних кілець. Обґрунтовано значення даної теми. Розглянуто властивості кілець, графи дільників яких мають певний тип: однорідні, ейлерові, дводольні, повні дводольні. Результати можуть бути використані при читанні спецкурсів із алгебри, особливо з теорії кілець.

ВЛАСТИВОСТІ ГРАФІВ ДІЛЬНИКІВ НУЛЯ РІЗНИХ КІЛЕЦЬ

ВИСНОВКИ

У кваліфікаційній роботі були розглянуті графи, вершинами яких є дільники нуля заданого скінченного кільця. Розглянуто необхідні для викладу матеріалу поняття: «кільце», «граф», «дільник нуля», «граф дільників нуля», «стиснений граф дільників нуля», побудовані приклади графів дільників нуля для різних скінченних кілець. Також було обґрунтовано значення даної теми. Розглянуті властивості кілець, графи дільників нуля яких мають певний тип: однорідні, ейлерові, дводольні, повні дводольні. Також були побудовані звичайні та стиснені графи дільників нуля для кілець конгруентності за модулем 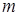, кільця верхньотрикутних матриць другого порядку над кільцем конгруентності за модулем 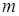. Самостійно вдалось отримати загальний вигляд індексів для повного дводольного графа дільників нуля кільця конгруентності за модулем 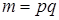, де 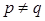 і p , q - прості числа, а також побудувати графи дільників нуля для кілець, які є прямим добутком кілець конгруентності за модулем  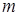та графи дільників нуля для нільпотентних кілець.

Результати можуть бути використані при читанні спецкурсів з алгебри, особливо з теорії кілець, для знайомства із задачами теорії графів, зокрема із книжковими вкладеннями графів, для ознайомлення із застосуваннями у інших галузях знань, зокрема в біології, генетиці.

ПЕРЕЛІК ПОСИЛАНЬ

1. Akbari S. When a zero-divisor graph is planar or a complete r-partite graph [Текст] / S. Akbari, H.R. Maimani, Yassemi

2. Akbari S.  On zero-divisor graphs of finite rings [Текст] / S. Akbari, H.R.Maimani - J. Algebra  314, 2007.

3. Akbari S. On the zero-divisor graph of a non-commutative ring [Текст] / S. Akbari, H.R. Maimani - J. Algebra  274, 2004.

4. Akbari S. On the zero-divisor graph of a commutative ring [Текст] / S. Akbari, H.R. Maimani - J. Algebra  274, 2004.

5. Anderson, The zero-divisor graph of a commutative ring. [Текст] /  D. Anderson, David F. and Livingston, S. Philip  - J. Algebra 217 ,1999.

6. Anderson D. Beck’s coloring of a commutative ring [Текст] /  D. Anderson , D. Naseer - Algebra 159, 1993.

7. Aihua Li Zero divisor graphs of upper triangular matrix rings [Текст] / Aihua Li and Ralph P. Tucci - 2013.

8. Beck I. Coloring of commutative rings [Текст] / Ivar Beck- J. Algebra 116 (1), 1988.

9. Belshoff R. Planar zero-divisor graphs [Текст] / R. Belshoff, J. Chapman - J. Algebra 316 (1), 2007.

10. Bollobas B. Graph theory: an introductory course [Текст] / Bela Bollobas- 1979.

11. Kuz’mina A.S. Nilpotent finite rings with planar zero-divisor graphs [Текст] /  A.S. Kuz’mina, Yu.N Maltsev -  Asian-European J. Math.1 (4), 565–574 (2008).

12. Кузьмина А.С. Описание конечных ненильпотентных колец, имеющих планарные графы делителей нуля [Текст] /  Кузьмина Анастасия Сергеевна- Дискретная математика 4, 2009.

13. Кузьмина А.С. О строении колец с планарными графами делителей нуля [Текст] / Кузьмина Анастасия Сергеевна - 2009.

14. Кузьмина А.С. Конечные кольца, нильпотентные графы которых являются однородными [Текст] / А.С. Кузьмина, Ю.Н. Мальцев - 2015.

15. Кузьмина А.С. Конечные кольца с полными двудольными графами делителей нуля [Текст] / А.С. Кузьмина, Ю.Н. Мальцев - 2012.

16. Кузьмина А.С., Finite rings with Eulerian zero-divisor graphs [Текст] / Кузьмина Анастасия Сергеевна  - J. of Algebra 2012.

17. Кузьмина А.С. Describing ring varieties in which all finite rings have

Hamiltonian zero-divisor graphs [Текст] / А.С. Кузьмина, Ю.Н. Мальцев - 2013

18. Thomas McKenzie Book embeddings and zero divisors [Текст] /  Thomas McKenzie, Shannon Overbay Ars -  Combinatoria, 2010.

19. Nazar H. Shuker The zero divisor ideal graph of the ring Z_N [Текст] / Nazar H. Shuker, Payman A. Rashed - 2015.

20. Weber D. Zero-Divisor Graphs and Lattices of Finite Commutative Rings[Текст] / David Weber -  2011.

ВСТУП

Для поняття "граф" немає загальновизнаного єдиного визначення. На математичній мові графом G (V, Е) прийнято називати сукупність непорожньої множини V елементів (вершин) і набору Е пар вершин (ребер). Нехай дана непорожня множина 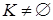 і на ній задані 2 алгебраїчні операції - додавання і множення. Нехай також виконуються наступні аксіоми:

а) ;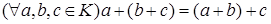

б) ;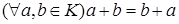

в) 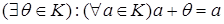. Елемент  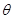називається нейтральним за додаванням (або нулем);

г) ;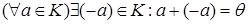

д) ;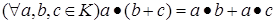

е) .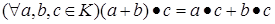

Тоді ця множина називається кільцем і позначається . Кільце називається асоціативним, якщо виконується така додаткова аксіома:

ж) .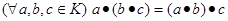

Якщо додатково виконується аксіома:

з) 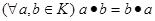, то кільце називається комутативним

Якщо в кільці :

и) 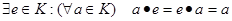, то елемент  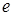називається нейтральним елементом по множенню (або одиницею кільця), а саме кільце називається кільцем з одиницею.

Якщо крім аксіом 1-8 виконується така умова:

к) 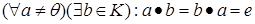, то кільце називають полем.

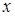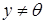Ненульовий елемент  кільця  називається лівим дільником нуля, якщо існує такий елемент , що 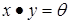. Аналогічно, ненульовий елемент кільця називається правим дільником нуля, якщо існує такий елемент 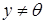, що 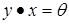. Елемент, який одночасно є і правим, і лівим дільником нуля, називається дільником нуля. Якщо множення в кільці комутативне, то поняття правого і лівого дільників нуля збігаються. Нуль називається невласним (тривіальним) дільником нуля. Відповідно, елементи, відмінні від нуля і є дільниками нуля, називаються власними (нетривіальними) дільниками нуля. Множину дільників нуля кільця  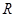прийнято позначати символом .

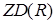У кваліфікаційній роботі розглядаються графи, вершинами яких є дільники нуля заданого скінченного кільця. Розглядаються необхідні для викладення матеріалу поняття: «кільце», «граф», «дільник нуля», «граф дільників нуля», «стиснений граф дільників нуля» будуються приклади графів дільників нуля для різних скінченних кілець. Обґрунтовано значення даної теми. Розглянуто властивості кілець, графи дільників яких мають певний тип: однорідні, ейлерові, дводольні, повні дводольні. Результати можуть бути використані при читанні спецкурсів із алгебри, особливо з теорії кілець.

ВИНИКНЕННЯ ІДЕЇ ПОБУДОВИ ГРАФА ДІЛЬНИКІВ НУЛЯ КІЛЬЦЯ ТА ЙОГО ЗАСТОСУВАННЯ

Поняття графа дільників нуля було введено в роботі [8]. І. Бек в 1986 ввів це поняття для комутативного асоціативного кільця і вершинами графа дільників нуля вважав усі елементи кільця. У 1999 р Д. Андерсон і Ф. Лівінгстон в роботі [5] дещо змінили спосіб побудови графа дільників нуля: вершинами графа вважалися всі дільники нуля комутативного кільця. На думку цих авторів, таке визначення краще ілюструє структуру множини дільників нуля кільця. У статті [4] визначення було змінено в такий спосіб. Як вершин графа дільників нуля комутативного асоціативного кільця автори роботи розглядали лише ненульові дільники нуля. Потім поняття графа дільників нуля було поширене і на некомутативний випадок [3]. В роботі [12] вперше стали досліджуватися графи дільників неасоціативних кілець. Одним з напрямків досліджень в цій області став опис кілець, граф дільників нуля яких задовольняє певній умові. Так, в роботах [3, 6, 11, 12] повністю описані скінченні асоціативні кільця з планарними графами дільників нуля. В [16] описані скінченні асоціативні кільця, що мають ейлерові графи дільників нуля. Також були описані скінченні кільця з повними дводольними графами дільників нуля [3]. На даному етапі розвитку теорії кілець не існує повного опису кілець з гамільтоновими графами дільників нуля. В роботі [4] отримано опис скінченних розкладених комутативних кілець з одиницею, графи дільників нуля котрих гамільтонові. Пізніше, в статті [3] цей результат був узагальнений на некомутативний випадок. Більш того, в роботі [3] повністю описано різноманіття асоціативних кілець, в яких всі скінченні кільця мають гамільтонові графи дільників нуля. Однак, повного опису скінченних асоціативних кілець з гамільтоновими графами дільників нуля поки немає. Відома теорема Дірака про те, що будь-який граф, в якому ступінь кожної вершини не менше числа n / 2, де n - число вершин в даному графі, причому n ≥ 3, є гамільтоновим [12]. В роботі [17] досліджуються властивості асоціативних кілець, графи дільників нуля яких задовольняють умові теореми Дірака. Зокрема, повністю описані кінцеві асоціативні кільця з одиницею, графи дільників нуля яких задовольняють умові теореми Дірака. Крім того, в статті [14] наведено опис скінченних асоціативних кілець з однорідними графами дільників нуля. У статті [11] доведено, що скінченні альтернативні нільпотентні кільця з планарними графами дільників нуля асоціативні.