РІЗНІ ОЗНАЧЕННЯ ГРАФА ДІЛЬНИКА НУЛЯ ТА ПРИКЛАДИ ПОБУДОВИ

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

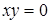Означення 2.1 Графом дільників нуля кільця R називається граф Γ(R), вершинами якого є всі ненульові дільники нуля цього кільця (односторонні і двосторонні), причому дві різні вершини з'єднуються ребром тоді і тільки тоді, коли або .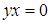

Для того, щоб навести перші приклади графів дільників нуля, введемо кілька важливих визначень.

Означення 2.2 Класом рівності(конгруенціями) за модулем m називають множину цілих чисел, що дають однакові залишки при діленні на m.

Множину класів рівності за модулем m позначають символом 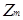. За означенням 2.2 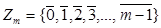. Над конгруенціями можна здійснювати звичайні операції додавання і множення, наприклад, за наступними правилами:

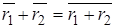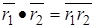; . (2.1)

Наведемо доведення факту, що множина конгруенцій утворює комутативне кільце з одиницею. Для цього перевіримо, що ця множина замкнена щодо введених операцій і що виконуються 8 аксіом:

а) ,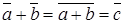

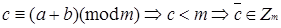
б) ,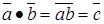

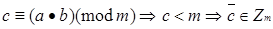
Додавання конгруенцій асоціативне і комутативне. Існує нейтральний за додаванням елемент 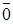. Існує протилежний елемент 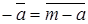такий, що 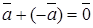. Множення конгруенцій також асоціативно і комутативне. Існує нейтральний за множенням елемент 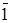такий, що .

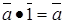Означення 2.3 Множина конгруенцій за модулем m з операціями додавання і множення, які визначені формулами (2.1), називається кільцем класів рівності(конгруентності) за модулем m і позначається .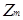

Розглянемо в якості першого прикладу конгруентність по модулю 30:

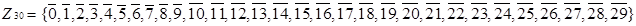
Побудуємо граф дільників нуля для кільця 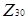. Відповідно до даного вище означення, усі ненульові дільники нуля будуть вершинами шуканого графа. За означенням дільника нуля, в даному кільці безліч дільників нуля має вигляд:

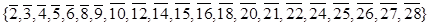
Зобразимо граф дільників нуля для вибраного нами кільця. Кільце конгруентності за модулем m є комутативним, тому граф дільників нуля такого кільця буде неорієнтованим. Сполучатимемо ребрами ці елементи між собою тоді і тільки тоді, коли 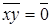, або .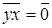

Означення 2.4 Неорієнтованим графом називається множина як завгодно розміщених на площині точок, деякі з яких сполучені відрізками або дугами.

Означення 2.5 Орієнтований граф (орграф) - це граф, ребрам якого присвоєний напрям. Спрямовані ребра іменуються також дугами.

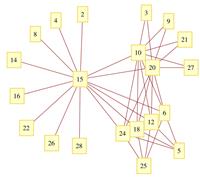
Рисунок 2.1 Граф дільників нуля кільця 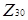(або )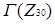

Аналогічним чином побудуємо ще декілька прикладів графів дільників нуля. Візьмемо, наприклад, кільця 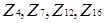. Можна вважати, що ці приклади дають різні випадки. Індекси 4 і 16 є степенями простого числа 2, 7 - просте число, а 12 є прикладом цілого числа загального вигляду, його канонічний розклад має вигляд: 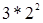. Для кільця 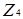єдиним дільником нуля є елемент 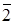. Кільце 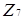є полем, оскільки число 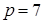є простим, а поле не має дільників нуля, тобто, якщо 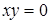, то 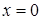або , або 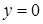, тобто граф дільників нуля такого кільця є порожнім. У кільці дільниками нуля є елементи 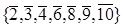, а в кільці 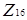- елементи 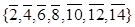. Побудуємо графи дільників нуля для цих кілець:

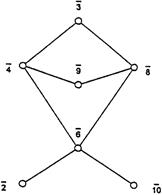
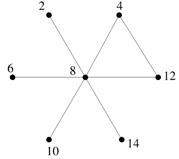
Рисунок 2.2 Графи дільників нуля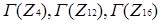

Покажемо вид графів дільників одного і того ж кільця при різних означеннях.

Приклад 2.2 Нехай 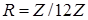, тобто маємо фактор-кільце кільця цілих чисел за його ідеалу.

Це кільце також можна розглядати як 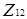. І. Бек в якості вершин графа дільників нуля таких кілець розглядав кожен елемент кільця :

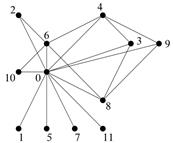
Рисунок 2.3 Граф дільників нуля за означенням І. Бека

Андерсон і Лівінгстон при побудові графа дільників нуля включали у множину вершин графа тільки дільники нуля кільця, кожен дільник нуля був окремою вершиною:

Рисунок 2.4 Граф дільників нуля за Андерсоном та Лівінгстоном

Означення 2.6 Анулятором елементу 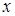комутативного кільця називається множина 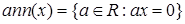, а сукупність таких множин для усіх елементів кільця називається анулятором кільця і позначається ann( ).

Означення 2.7 Елементи 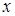і 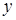кільця 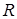називаються еквівалентними, якщо виконується умова 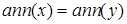. Позначається .

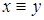Відношення 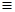є відношенням еквівалентності у кільці 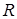, тому розбиває усе кільце на класи еквівалентності. Використовуючи це відношення, можна вивчати структуру множини дільників нуля, не зображуючи увесь граф дільників нуля. Це важливо особливо у випадках скінченних кілець з великою кількістю елементів.

Означення 2.8 Для кільця 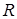стисненим графом дільників нуля називається граф, що означає 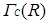, вершинами якого являються ненульові класи еквівалентності і 2 вершини 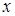і 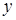, сполучені ребром тоді і тільки тоді, коли .

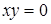Розглянемо як приклад знову кільце:

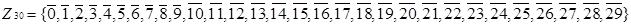
Побудуємо стиснений граф дільників нуля для кільця 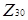. Знайдемо анулятори дільників нуля кільця. Наприклад, 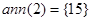, оскільки серед усіх елементів кільця 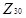тільки 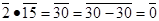, а 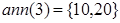оскільки 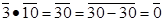та 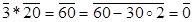. Аналогічним чином, знаходячи анулятори для усіх інших дільників нуля кільця 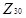, у результаті отримаємо:

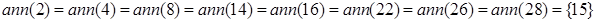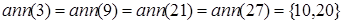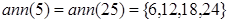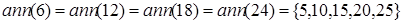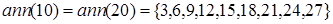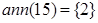Класами еквівалентності кільця будуть наступні множини:

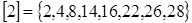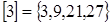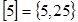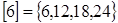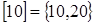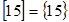За означенням, вершинами стисненого графа дільників нуля кільця 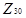будуть елементи: 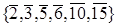. Сполучатимемо ребрами ці елементи між собою тоді і тільки тоді, коли 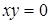. Як було відмічено вище, це кільце є комутативним, а тому його граф дільників нуля буде неорієнтованим. У результаті, маємо наступний граф:

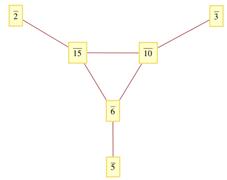
Рисунок 2.5 Стиснений граф дільників нуля для кільця

Для пояснення зв'язку між звичайним і стисненими графами дільників нуля, побудуємо ще 2 приклади, які включатимуть і звичайний граф дільників нуля, і його стиснений граф:

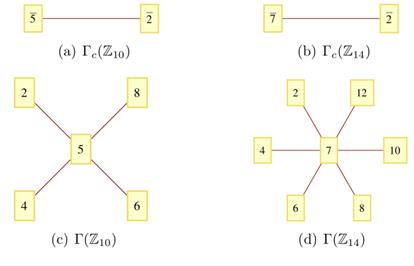
Рисунок 2.6 Звичайні (с,d) та стиснені (a,b) графи дільників нуля

для кілець 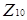и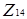

Зв'язок між звичайними і стисненими графами дільників нуля кільця описується наступною теоремою.

Теорема 2.1 Нехай і - скінченні комутативні кільця. Якщо 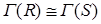, тоді .

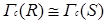Обернена теорема не завжди вірна, ми можемо бачити це безпосередньо з рис 3.2: стиснені графи дільників нуля 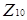і 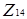ізоморфні, а звичайні - ні.

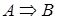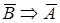Теорему можна ефективно використати для доказу неізоморфності графів дільників нуля двох кілець. Цей факт випливає з неізоморфності стиснених графів дільників нуля цих кілець. Дійсно, з математичної логіки відомо, що теореми і або одночасно істинні, або одночасно неправдиві.

Приклад 2.3 Розглянемо кільце верхньотрикутних матриць другого порядку 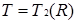над довільним комутативним кільцем з одиницею. В якості кільця виберемо кільце .

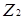Ненульовими дільниками нуля кільця 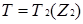є матриці:

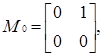
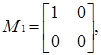
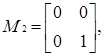
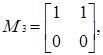
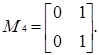
Побудуємо таблицю множення Келі для дільників нуля кільця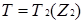

	M₀	M₁	M₂	M₃	M₄
M₀	0	0	M₀	0	M₀
M₁	M₀	M₁	0	M₃	M₀
M₂	0	0	M₂	0	M₂
M₃	M₁	M₁	M₀	M₃	0
M₄	0	0	M₄	0	M₄

Рисунок 2.7 Таблиця множення Келі

Побудуємо сам граф дільників нуля даного кільця :

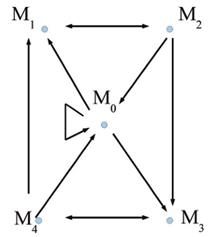
Рисунок 2.8 Граф дільників нуля для кільця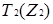

Лема 2.1 Нехай 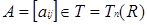, тоді 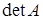також є дільником нуля в R тоді і тільки тоді, коли 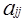- дільник нуля в R для деякого .

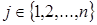Доведення. Це випливає із того факту, що для верхньотрикутних матриць 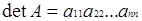. За означенням дільника нуля, 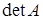є дільником нуля тоді і тільки тоді, коли 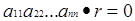для деякого ненульового 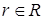. Нехай 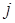таке, що: 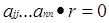, але 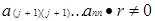. Тод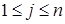і і 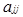- дільник нуля.

Означення 2.9 Нехай 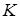- кільце с одиницею. Елемент 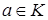називають одиничним, якщо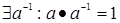

Теорема 2.2 .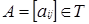

(1) Матриця 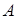- лівий і правий дільник нуля в 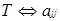- дільник нуля в R для деякого .

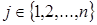(2) Якщо кожен елемент із R або одиничний, або дільник нуля, тоді кожен елемент із T або одиничний, або дільник нуля.

Теорема 2.3 У скінченному кільці з одиницею кожен ненульовий елемент або одиничний, або є дільником нуля.

Використовуючи лему 2.1 і теорему 2.2, сформулюємо і доведемо наступну теорему.

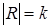Теорема 2.4. Нехай скінченне кільце, , і 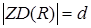, тоді:

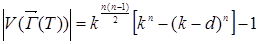Доведення. Потужність множини 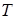дорівнює 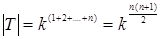, так як 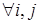елемент 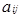приймає рівно 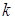значень, 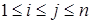. Так як потужність множини одиничних елементів кільця рівна 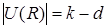, то можна підрахувати число одиничних елементів у кільці 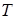. Відповідно до леми 2.1 на головній діагоналі можуть знаходитись тільки одиничні елементи кільця . Інші елементи матриць із 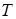можуть бути будь-якими елементами кільця . Тому:

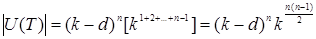де 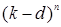- число можливих значень діагональних елементів, 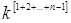- число можливих значень недіагональних елементів. Число дільників нуля у кільці 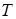дорівнює (відповідно до теореми 2.2 п.2) різниці:

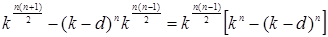Ця формула включає також і нульову матрицю, тому число ненульових дільників нуля на 1 менше ніж у отриманій формулі, що і потрібно було довести.

Дата: 2019-02-02, просмотров: 313.

⇐ Предыдущая 123 4 5 Следующая ⇒