Означення 3.3 Дводольний граф G  це граф, множину вершин V якого можна розбити на дві непустих підмножини V 1 й V2, що не перетинаються таким чином, що кожне ребро графа G з’єднує вершини із різних підмножин. Якщо дводольний граф G не містить кратних ребер і кожна вершина із множини V1 з’єднана з кожною вершиною із множини V2, то такий граф називають повним дводольним.
це граф, множину вершин V якого можна розбити на дві непустих підмножини V 1 й V2, що не перетинаються таким чином, що кожне ребро графа G з’єднує вершини із різних підмножин. Якщо дводольний граф G не містить кратних ребер і кожна вершина із множини V1 з’єднана з кожною вершиною із множини V2, то такий граф називають повним дводольним.
Теорема 3.4 Нехай R  скінченне кільце. Тоді Γ( R ) = Kn,m тоді і тільки тоді, коли R ізоморфне одному із наступних кілець:
скінченне кільце. Тоді Γ( R ) = Kn,m тоді і тільки тоді, коли R ізоморфне одному із наступних кілець:
(1) Z9 ;
(2) N0,3 ;
(3) Z3 [ x ] / ( x 2 );
(4) N2,2 ;
(5) N4 ;
(6) Z2 [ x ] / ( x 3 );
(7) Z4 [ x ] / (2 x, x 2 − 2);
(8) Z8 ;
(9) A2,  ;
;
(10) GF ( q 1 ) ⊕ GF ( q 2 );
(11) GF ( q 1 ) ⊕ N 0,2 ;
(12) GF ( q 1 ) ⊕ Z4 ;
(13) GF ( q 1 ) ⊕ Z2 [ x ] / ( x 2 ) .
Ця теорема доведена у роботі [15]. Побудуємо відповідні приклади.
Розглянемо у якості першого прикладу кільце 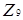 . За теоремою його граф дільників нуля буде дводольним графом Kn,m. Знайдемо значення індексів n та m. Ненульовими дільниками нуля у цьому кільці будуть елементи
. За теоремою його граф дільників нуля буде дводольним графом Kn,m. Знайдемо значення індексів n та m. Ненульовими дільниками нуля у цьому кільці будуть елементи 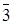 та
та 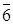 . В результаті отримаємо граф K1,1:
. В результаті отримаємо граф K1,1:
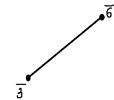
Рисунок 3.4  Г(
Г( 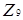 )
)
Означення 3.4 Лівим(правим) ідеалом кільця 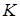 називається таке його підкільце
називається таке його підкільце 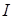 , що
, що 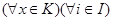
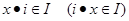
Лема 3.1 Нехай 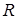 - скінченне кільце. Тоді наступні умови еквівалентні:
- скінченне кільце. Тоді наступні умови еквівалентні:
1. Множина 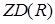 - ідеал;
- ідеал;
2. Будь який елемент 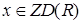 є нільпотентом кільця.
є нільпотентом кільця.
Повертаючись до попереднього прикладу, можна легко переконатись, що елементи 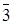 й
й 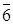 є нільпотентами для кільця
є нільпотентами для кільця 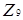 , а ідеал кільця, породжений
, а ідеал кільця, породжений 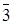 , також складається із елементів
, також складається із елементів 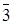 і
і 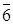 .
.
Визначимо відстань від кожної вершини графа до найдальшої від неї вершини: 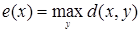 , яка називається ексцентриситетом.
, яка називається ексцентриситетом.
Означення 3.5 Максимальний ексцентриситет 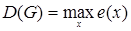 має назву діаметру графа, а мінімальний
має назву діаметру графа, а мінімальний 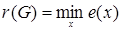 - радіусу графа.
- радіусу графа.
Означення 3.6 Вершина 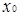 називається центральною, якщо
називається центральною, якщо 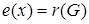 . Множину центральних вершин називають центром графа.
. Множину центральних вершин називають центром графа.
Лема 3.2 Нехай 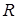 - скінченне кільце таке, що Г(R)=K 1,n з центром
- скінченне кільце таке, що Г(R)=K 1,n з центром 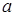 . Тоді наступні вимоги еквівалентні:
. Тоді наступні вимоги еквівалентні:
1. Множина 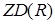 - ідеал;
- ідеал;
2. a2=0;
3. Кільце R ізоморфне кожному із кілець Z4, Z8, Z9, Z2[х]/(х2), Z2[х]/(х3), Z3[х]/(х2) и Z4[х]/(2х,х2-2).
Приклад 3.4 Розглянемо кільце
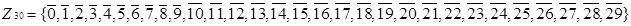
Запишемо ідеали даного кільця, породжені елементами 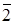 ,
, 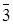 ,
, 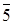 й
й 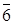 :
:
I1=( 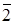 )= {0,2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28},
)= {0,2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28},
I2=( 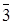 )={0, 3, 6, 9, 12, 15, 18, 21, 24, 27},
)={0, 3, 6, 9, 12, 15, 18, 21, 24, 27},
I3=( 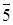 )={0, 5, 10, 15, 20, 25},
)={0, 5, 10, 15, 20, 25},
I4=( 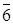 )={0, 6, 12, 18, 24}.
)={0, 6, 12, 18, 24}.
Усі вони за означенням ідеалу є кільцями, тому можна розглядати задачу про знаходження графів дільників нуля цих ідеалів. Нехай 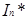 - множина дільників нуля ідеалу
- множина дільників нуля ідеалу 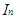 , тоді
, тоді
I1*=( 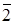 )= { 6, 10, 12, 18, 20, 24},
)= { 6, 10, 12, 18, 20, 24},
I2*=( 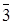 )={ 6, 12,15, 18, 24},
)={ 6, 12,15, 18, 24},
I3*=( 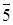 )={ 10, 15, 20},
)={ 10, 15, 20},
I4*=( 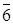 )={0}.
)={0}.
Графи дільників нуля цих ідеалів, що позначаються ГI1(Z30), ГI2(Z30), ГI3(Z30), мають наступний вигляд:
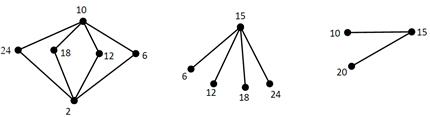
Рисунок 3.5  Графи дільників нуля ідеалів кільця
Графи дільників нуля ідеалів кільця 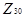
Теорема 3.5 Нехай дано кільце 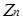 , де
, де 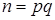 , p і q - прості. Якщо p і q різні, то граф дільників нуля такого кільця буде повним дводольним.
, p і q - прості. Якщо p і q різні, то граф дільників нуля такого кільця буде повним дводольним.
Приклад 3.5 Кільце 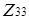 задовольняє умові теореми 3.5, так як
задовольняє умові теореми 3.5, так як 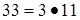 , отже граф дільників нуля є повним дводольним і має вигляд:
, отже граф дільників нуля є повним дводольним і має вигляд:
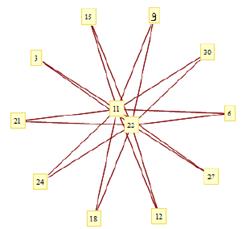
Рисунок 3.6  Граф
Граф 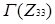 =К2,10 дільників нуля кільця
=К2,10 дільників нуля кільця 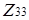
Аналогічно, для усіх 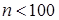 й рівних одному із наступних значень: 6; 10; 14; 15; 21; 22; 26; 33; 34; 35; 38; 39, 46, 51, 55, 57, 58, 62, 65, 69, 74, 77, 82, 85, 86, 87,91,93,94,95 графи дільників нуля для кільця
й рівних одному із наступних значень: 6; 10; 14; 15; 21; 22; 26; 33; 34; 35; 38; 39, 46, 51, 55, 57, 58, 62, 65, 69, 74, 77, 82, 85, 86, 87,91,93,94,95 графи дільників нуля для кільця 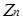 будуть повними дводольними графами.
будуть повними дводольними графами.
Наслідок 3.1 Граф дільників нуля кільця 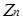 , де
, де 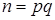 , p і q – прості, є повним дводольним виду
, p і q – прості, є повним дводольним виду 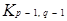 .
.
Дата: 2019-02-02, просмотров: 307.