Составной оператор используется в том случае, когда по правилам синтаксиса сложного оператора должен стоять только один оператор, а в алгоритме необходимо выполнить некоторую последовательность действий. Составной оператор объединяет эту последовательность в единый по синтаксису оператор путем заключения в операторные скобки begin и end. Например:
ВEGIN
<оператор1>;
<оператор2>;
. . . ;
<операторN>
END;
Для составного оператора допускается любая глубина вложенности:
BEGIN
BEGIN
. . .
BEGIN
. . .
END;
. . .
END;
END ;
Пустой оператор не выполняет никаких действий и может быть использован для передачи управления в конец составного оператора. Пустой оператор записывается в виде точки с запятой.
Например, пустыми операторами будут следующие записи:
1) ; ; 2) <метка>: ;
Оператор безусловного перехода
Оператор безусловного перехода позволяет изменить обычный последовательный порядок выполнения операторов и непосредственно перейти к нужному оператору, предварительно помеченному меткой.
Структура такого оператора:
GOTO <метка>;
где GOTO - ключевое слово, обозначающее перейти к <метке>,
<метка> является произвольным идентификатором, который позволяет пометить любой оператор в программе и потом ссылаться на него. Оператор от метки отделяется двоеточием. В языке Pascal ABC допускается использовать в качестве метки также целое число без знака.
Пример:
LABEL m1, loop;
VAR a, b, c, d: word;
BEGIN
m1: a := b+c*d;
. . .
goto m1;
loop: END .
Все использованные в программе метки должны быть описаны в разделе описаний программы с указанием ключевого слова “LABEL”. Описанные в этом операторе метки обязательно должны быть использованы в программе.
Метки, описанные в функции или процедуре, локализуются только в ней, передача управления извне процедуры на метку внутри ее невозможна. С помощью оператора GOTO не рекомендуется осуществлять переход во внутреннюю часть сложного оператора (цикла, составного оператора). Запрещается переход с одной альтернативной части (ветви) сложного оператора на другую.
Современная технология структурного программирования основана на принципе программирования без GOTO. Считается, что злоупотребление этими операторами затрудняет чтение программы, усложняет ее отладку.
Тем не менее, в некоторых случаях использование оператора перехода может упростить программу. Обычно GOTO используется для досрочного выхода из любого сложного оператора или вложенных операторов цикла.
4.5. Пример и задания с оператором IF
Пример. Вычислить значения функции y( x) в зависимости от интервала, в который попадает аргумент x.
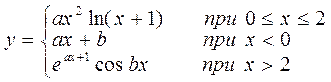 Для xÎ [-10,5]
Для xÎ [-10,5]
где а = 1.5, b = 0.5 ;
Напишем программу, соответствующую схеме алгоритма (рис. 5):
Program Lr2;
Label m1, 10;
Const A = 1.5; B = 0.5;
var x, y: real; // переменные вещественного типа
Begin
m1: read(x); // вводим значение переменной x
IF (x < -10) or (x>5) then goto m1;
IF x<0 then begin y:= a*x+b ; goto 10 end ;
if (x >= 0) and (x<=2) then y :=A*SQR(x)*LN(x+1) ;
if x>2 then y := EXP(A*x+1)*COS(B*x);
10: writeln( ' x= ', x :8:1 , ' y= ' , y :8:2); //вывод значений x и y
End.




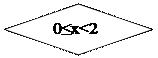









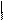
|
|


|
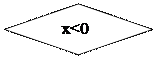
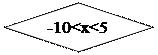




|
|
|
|
|
|
Рис. 5
Задания к самостоятельному выполнению (программа_2_1)
Вычислить значение функции в зависимости от интервала, в который попадает вводимый с клавиатуры аргумент:
 1. Для t
1. Для t  [0,3], at2lnt при 1 £ t £ 2,
[0,3], at2lnt при 1 £ t £ 2,
где a = -0.5,b = 2 z = 1 при t < 1,
eatcosbt при t > 2,
 2. Для x
2. Для x 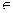 [0,4],
[0,4], 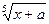 при x > 2,
при x > 2,
где а = 2.3 f = х при 0.3 < x £ 2,
cos(x-a) при x £ 0.3,
 |
3. Для x 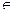 [0,7], (a+b)/(ex+cosx) при 0 £ x < 2.3,
[0,7], (a+b)/(ex+cosx) при 0 £ x < 2.3,
где a = -2.7,b = -0.27 z = (a+b)/(x+1) при 2.3 £ x < 5,
ex+sinx при 7 ³ х ³ 5,
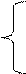 4. Для i
4. Для i 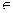 [7,12], ai4+bi при I < 10,
[7,12], ai4+bi при I < 10, 
где a = 2.2,b = 0.3. y = tg(i+0.5) при I = 10,
e2i+ 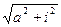 при I > 10,
при I > 10,
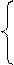 5. Для x
5. Для x 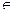 [0.9,5],
[0.9,5], 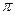 x2-7/x2 при x < 1.3,
x2-7/x2 при x < 1.3,
где a = 1.5 y = ax3+7 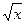 при 1.3 £ x < 3,
при 1.3 £ x < 3,
lg(x+7 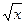 ) при x ³ 3,
) при x ³ 3,
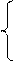 6. Для t
6. Для t 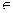 [-1.4],
[-1.4], 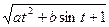 при t < 0.1,
при t < 0.1,
где a = 2.1,b = 0.37. z = at+b при 0.1 £ t < 2,
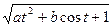 при t ³ 2,
при t ³ 2,
 7. Для x
7. Для x 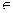 [0,6], a esinx+2.5 при x < 0.3,
[0,6], a esinx+2.5 при x < 0.3,
где a = 1.5. y = ecosx+a при 0.3 £ x < 4,
(sin x)/(a+ex) при x ³ 4,
|
 8. Для x
8. Для x 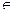 [1,2], a/x+bx2-c при x £ 1.2,
[1,2], a/x+bx2-c при x £ 1.2,
где a = 1.8,b = -0.5, c = 3.5 (a+bx)/ 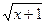 при x > 1.2,
при x > 1.2,
 9. Для t
9. Для t 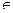 [1,5], t
[1,5], t 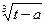 при t > a,
при t > a,
где a = 2.5 z = t sin at при t = a,
e-at cos at при t < a,
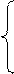 10. Для x
10. Для x 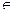 [0,4], e-bx sin bx при x < 2.3,
[0,4], e-bx sin bx при x < 2.3,
где a = 1,b = 3 y = сos bx при 2.3 £ x £ 3,
e-ax cos bx при x ³ 3,
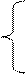 11. Для t
11. Для t 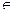 [0.5,3], at2-b
[0.5,3], at2-b 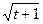 при t < a,
при t < a,
где a = 1.3, b = 6.5 z = a-b при a £ t £ b,
a t2/3- 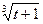 при t > b,
при t > b,
 |
12. Для x 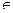 [0,2], |e-2x sin bx| при x >1,
[0,2], |e-2x sin bx| при x >1,
где b = -2.9 y = cos bx при x = 1,
e-x cos bx при x < 1,
 13. Для x
13. Для x  [0.5,2] sin (cos ax) при x >1,
[0.5,2] sin (cos ax) при x >1,
где a = -0.8 z = tg ax при x = 1,
a2 x при x < 1,
 14. Для x
14. Для x  [1,2], ln bx - 1/(bx+1) при x < 1.3,
[1,2], ln bx - 1/(bx+1) при x < 1.3,
где b = 1.3 y = bx + 1 при 1.3 ³ x ³ 1.7,
ln bx +1/(bx+1) при x > 1.7,
 |
15. Для x 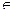 [-1,1], ax2+bx2/3 при x < 0.1,
[-1,1], ax2+bx2/3 при x < 0.1,
где a = 2.5,b = -0.9 z = a x2 при x = 0.1,
b x2/3 при x > 0.1.
16. Ввести координаты точки (x, y). Напечатать, в каком квадранте или на какой оси координат находится эта точка.
17. Ввести радиусы R1, R2 и высоту. Вычислить объем усеченного конуса: 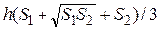 , где S – площадь оснований. Если R1 = R2 – объем и площадь цилиндра, если R1 = 0 или R2 = 0 – объем (hπr2) и площадь πr(
, где S – площадь оснований. Если R1 = R2 – объем и площадь цилиндра, если R1 = 0 или R2 = 0 – объем (hπr2) и площадь πr( 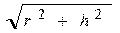 ) поверхности конуса.
) поверхности конуса.
18. Ввести с клавиатуры цифру. Определить, какой системе счисления она может принадлежать.
19. Ввести число. Определить, делится ли оно нацело на два, три или на пять.
20. Ввести a, b, h. Если h = 0, вычислить площадь прямоугольника; при a = b, найти площадь квадрата; в противном случае подсчитать площадь трапеции.
4.6. Оператор выбора варианта CASE
Оператор CASE позволяет в зависимости от значения какой-либо переменной или выражения порядкового типа выполнить те или иные действия.
Его структура имеет следующий вид:
CASE <ключ_выбора> OF
<константа_выбора1>: <оператор1>;
<константа_выбора2>: <оператор2>;
. . .
<константа_выбораN>: <операторN>
ELSE <оператор>
END;
где <ключ_выбора> - переменная (или выражение) любого порядкового типа; <константа_выбора> - константа того же типа, что и <ключ_выбора>; <оператор> - произвольный оператор Pascal ABC.
Принцип действия оператора. Сначала вычисляется <ключ_выбора>, затем в списке констант выбора отыскивается нужная константа, равная <ключу_выбора>, и выполняется стоящий за ней оператор. После этого оператор CASE завершает работу. Если в списке не найдена константа, совпадающая с "ключом", выполняется оператор, стоящий после ELSE.
Заметим, что стоящая в конце часть ELSE <оператор> является не обязательной. При отсутствии в списке выбора нужной константы оператор выбора просто завершает свою работу.
Любому из операторов <списка выбора> может предшествовать несколько <констант выбора>. В этом случае они разделяются запятыми или представляют собой диапазон значений.
Пример:
CASE <ключ> OF
1: <оператор1>;
2, 3: <оператор2>;
4 .. 6: <оператор3>
ELSE <оператор>
END;
<Константа_выбора> не является меткой оператора, поэтому в разделе меток описывать её нельзя.
4.7. Примеры и задания с оператором CASE
Пример 1. Выполнить арифметическую операцию в зависимости от введенного с клавиатуры символа.
VAR operation: char;
x, y, z: real;
BEGIN
read(x,y);
read (operation);
CASE operation OF
'+': z:=x+y;
'-': z:=x-y;
'*': z:=x*y;
'/': z:=x/y;
ELSE write('нет опеpаций')
END;
WRITELN( ' z= ' , z )
END.
 Пример 2. Составить программу для начисления зарплаты согласно следующему правилу: если стаж работы сотрудника менее пяти лет, то зарплата равна 50$, при стаже работы от пяти до 15 лет – 100$, свыше 15 лет зарплата повышается с каждым годом на 10$, причем при стаже, превышающем 30 лет, она составляет 300$.
Пример 2. Составить программу для начисления зарплаты согласно следующему правилу: если стаж работы сотрудника менее пяти лет, то зарплата равна 50$, при стаже работы от пяти до 15 лет – 100$, свыше 15 лет зарплата повышается с каждым годом на 10$, причем при стаже, превышающем 30 лет, она составляет 300$.
Для программирования решения этой задачи определим математическую формулировку задачи:
 50, если ST < 5;
50, если ST < 5;
|
100 + (ST -15)*10 при 15 < ST ≤ 30;
300, если ST > 30;
где ZP – зарплата, ST – стаж работы.
Реализация задачи для примера 2
представлена следующим алгоритмом
(рис. 6) и программой:
Program zarplata;
var ST: byte; {стаж (байтовый) тип)}
|
Begin
writeln('введите стаж');
read(ST); {ввод стажа}
case ST of {выбор из }
1..4: ZP:=50;
5..15: ZP:=100;
16..29: ZP:=100+(ST-15)*10
else ZP:=300
end;
writeln(' Зарплата = ' , ZP:10:2,' $'); {вывод результата}
End.
Задания к самостоятельному выполнению (программа 2_2)
1. Определить остаток от деления на восемь введенного числа х и написать восьмеричную цифру прописью.
2. По цифре (0..9), введенной с клавиатуры, напечатать название этой цифры.
3. С клавиатуры ввести число k (1..30). Определить, какому дню недели оно соответствует, если первое число – понедельник.
4. Ввести число и номер месяца. Напечатать дату с названием месяца прописью.
5. Идет k секунда суток. Вычислить, сколько прошло часов и полных минут к этому моменту, при этом согласовать со значением слова (час, часа, часов, минута, минуты, минут).
6. В зависимости от номера (N) типа фигуры организовать ввод необходимых данных и вычислить при N = 1 – площадь круга, N = 2 – объем шара (4/3πR3), N = 3 – объем цилиндра, N = 4 – площадь поверхности сферы 4πr2.
7. Ввести число N (0 ≤ N ≤ 15). Определить и напечатать шестнадцатеричную цифру, ему соответствующую.
8. Для целого числа R (1…99) напечатать фразу « Мне R лет », при некоторых значениях R слово «лет» заменить словом «год» или «года».
9. В зависимости от заданного номера фигуры ввести необходимые данные и вычислить при к = 1 площадь прямоугольника, при к = 2 площадь параллелограмма, а при к = 3 площадь трапеции по формуле (a+b) h/2. Во втором случае напечатать: является ли фигура параллелограммом или ромбом.
10. Перевести введенное целое число 0 ≤ х ≤ 31 в шестнадцатеричную систему счисления.
5. ПРОГРАММИРОВАНИЕ АЛГОРИТМОВ
ЦИКЛИЧЕСКОЙ СТРУКТУРЫ
5.1. Оператор счётного цикла
В языке Pascal существует три разновидности операторов цикла:
1) счетный оператор цикла (оператор цикла со счётчиком);
2) оператор цикла с предусловием;
3) оператор цикла с постусловием.
Для любого оператора цикла вход в цикл возможен только через его начало, выход осуществляется как вследствие естественного окончания цикла, так и путем выполнения оператора перехода GOTO или процедур выхода, содержащихся внутри цикла.
Счетный оператор цикла FOR реализует циклический процесс с известным числом повторений. Этот оператор имеет две формы записи. Первая форма позволяет наращивать <параметр цикла> на единицу и имеет вид
FOR <параметр_цикла> :=<min_значение> TO <max_значение>DO<оператор>;
Параметром цикла называется переменная, служащая для управления циклом. Для оператора цикла FOR в качестве <параметра_цикла> используется переменная целого либо любого порядкового типа. Здесь <min_значение> и <max_значение> - это константы (или выражения), определяющие соответственно начальное и конечное значения параметра цикла. Их типы должны быть совместимыми с типом параметра цикла.
Вторая форма позволяет уменьшать на единицу значение параметра цикла:
FOR <параметр цикла> := <max значение> DOWNTO
<min значение> DO <оператор>;
Пример. Вычислить Y = 1 + 1/2 + 1/3 + ... + 1/N.
Для вычисления в программе необходимо многократно произвести сложение по “формуле суммы” Y =Y+1/I при изменении параметра I от одного до N.
Реализация 1: Y:=0;
FOR I:=1 TO N DO Y=Y+1/I;
Реализация 2: Y:=0;
FOR I:=N DOWNTO 1 DO Y=Y+1/I;
Значение параметра цикла в теле цикла может не использоваться, а лишь выполнять функцию счетчика. Например, пусть необходимо вычислить Y = Xn. Тогда фрагмент тела программы запишется в следующем виде:
Y:=1;
FOR I :=1 TO N DO Y=Y*X;
Два других оператора цикла (с пpедусловием и постусловием) проверяют условия повторения или окончания цикла, но сами не изменяют значения параметра цикла. Они организуют выполнение цикла с неизвестным заранее числом повторений.
Примеры и з адания для оператора цикла со счётчиком
Пример1. Вычислить сумму членов ряда: s = 1 +1/4 +1/9+ 1/16 + ... .
Учитывая, что параметр - знаменатель числового ряда – изменяется как квадрат натурального числа, определим алгоритм решения задачи в виде циклической структуры (pис. 7) и напишем соответствующую программу:
PROGRAM summa;
VAR s, r: REAL;
 i, N: INTEGER;
i, N: INTEGER;
BEGIN
s:=0;
WRITELN('введите N');
READ(N);
FOR I :=1 TO N DO
begin
r := 1/sqr(i);
s := s + r;
end;
WRITELN( ' Сумма= ' , s:6:2 );
END .
Пример 2. Вычислить значения двух функций F1(x) = tg (x) и F2(x) = sin(x) в n точках, равномерно распределенных на интервале a ≤ x ≤ b, где a = -π/4, b = π.
 Для реализации данной задачи разработана схема алгоритма (pис. 8) и cледующая программа:
Для реализации данной задачи разработана схема алгоритма (pис. 8) и cледующая программа:
Program Lab3;
Const а = -pi/4; b = pi;
Var F1, F2, x, dx: real; {dx – шаг изменения х}
i, n: integer; {i – параметр цикла}
Begin
writeln ('введите число точек N'); read(n);
dx: = abs(b-a)/(n-1);
x:=a;
writeln (' ___________________________');
writeln ('| I | X | F1 | F2 |');
writeln ('|---|------------|------------|------------|');
for I := 1 to n do {опеpатоp цикла}
Begin
F2:= sin(x);
F1:= F2/cos(x); {вычисление tg x}
writeln('|', i:3,' |', x:8:3,'|', f1:8:4,' |', f2:8:4,' |');
|
end;
writeln( ' | ________________________| );.
End .
Задания к самостоятельному выполнению
Задание 1 (программа_3_1)
Для заданных с клавиатуры значений переменных x и n вычислить:
1. X = 1 + 1/2 + 1/3 + ... + 1/10. 2. Z = 2 × 4 × 6 × 8 × ... × 20.
3. Y = -x + 4x - 9x + ... - 81 x. 4. Y = x + x/3 + x/5 + ... + x/17.
5. Y = n! = 1× 2 × 3 × ....n. 6. Y = 1 - 3 + 32 - 33 + . . . + 310.
7. Y= 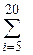 x2 / ( 2i-1). 8. Z =
x2 / ( 2i-1). 8. Z = 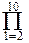 ( x+i) / i.
( x+i) / i.
9. Y = 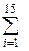 x2/i. 10. Y = 1 + x/2 + x2/4 + x3/6 + ... + xi/2i + ... + x9 /18 .
x2/i. 10. Y = 1 + x/2 + x2/4 + x3/6 + ... + xi/2i + ... + x9 /18 .
11. Y = 1 + x2/1! + x4/2! + x6/3! + … + x20/10! = 1+ 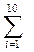 x2i/i!.
x2i/i!.
12. Y = 1 - x + x3/3! - x5/5! + ... + (-1)n x2n-1/(2n-1)! + ... + x11/11!.
13. е = 1 + 1/1! + 1/2! + ... + 1/n! + ... (сравнить результат со значением функции EXP(1), определенной в Паскале).
14. π = 4(1 - 1/3 + 1/5 - 1/7 + … + (-1)n/(2n+1) + …) (результаты сравнить с определенным в языке Паскаль числом Pi).
15. Y = arctg x = x-x3/3 +x5/5- ... +(-1)n x2n+1/(2n+1)+ ... (|х|<1).
16. Z = LN(1+x) = x - x2/2 + x3/3 - ... + (-1)n-1 xn/n + ... (|x|<1).
17. S = x - x3/3! + x5/5! - ... +(-1)n x2n+1/(2n+1)! + ... .
18. Вычислить суммы положительных и отрицательных значений функции
z = cos(nx+a) sin(nx-a),
где n =1, 2, ... , 5, a и x - вещественные числа.
19. Вычислить сумму четных и сумму нечетных чисел натурального ряда
в диапазоне от 1 до N.
20. Найти сумму факториала 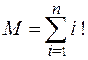 .
.
Задание 2 (программа_3_2)
Вычислить значения двух функций в n точках, равномерно распределенных в диапазоне а ≤ x ≤ b. Результаты оформить в виде таблицы.
| № п/п | a | b | n | F1(х) | F2(х) |
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 | 0
1
-1
-2
0
-  -1
-4
1
1
0
-
-1
-4
1
1
0
-  0
1
2
2
0
1
3
1
0
1
2
2
0
1
3
1
| 2
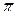 2
5
5
2
5
5
 3
4
3
4
2
3
4
3
4
2
 2
4
4
5
3
2
4
4
5
3
| 20 18 15 14 16 20 20 12 15 20 20 18 16 12 10 16 18 20 15 18 | sin x cos x
1+2x+5
4e-|x|-1
| x+10|5
2 sin 2x +1
2-cos x
2x/10
x3e2x
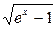 1/(1+
1/(1+ 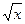 )
5-3 cos x
|sinx|+|cosx|
e-x+cos2x
e-x lg )
5-3 cos x
|sinx|+|cosx|
e-x+cos2x
e-x lg 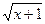 x cos x/2
2x lg x - 3x lg x
3-x/50
e2x
x cos x/2
2x lg x - 3x lg x
3-x/50
e2x 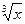 - sin x
2x arctg x - 5 - sin x
2x arctg x - 5 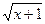 1,5arctg x 1,5arctg x
| sin x + cos x -1
(x-1)3
cos x
e-(x+5)
(x+5)3(1+sin2x)
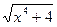 20/(1+x2)
ex sin x
x ln2 x
2x/(1-4x)
20/(1+x2)
ex sin x
x ln2 x
2x/(1-4x)
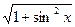 |sin x| - |cos x|
e -2x
x + sin x
|sin x| - |cos x|
e -2x
x + sin x
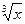 + + 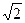 e -x
ctg x
x e -x +ln x
10/(2+x2)
e -ахx
е2x lg x - 3ax e -x
ctg x
x e -x +ln x
10/(2+x2)
e -ахx
е2x lg x - 3ax
|
Дата: 2019-02-02, просмотров: 401.