Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Оператор цикла с предусловием используется в случае, когда число повторений цикла заранее не известно. При этом цикл управляется условием, записанным в начале цикла, и поэтому действия в цикле при некотором условии могут ни разу не выполниться. Структура этого оператора имеет вид

WHILE <условие> DO <оператор>;

где <условие> – это любое логическое выражение для параметра цикла, истинность которого проверяется в начале каждой итерации (условие выполнения тела цикла), <оператором> может быть произвольный оператор языка, в том числе и составной.

Правило выполнения оператора цикла с предусловием. Если <условие> истинно, то выполняется <оператор>, стоящий за ключе­вым словом DO, если <условие> ложно, то происходит выход из цикла и выполняется следующий оператор программы. После выполнения <оператора> вновь вычисляется и анализируется <условие>, и вновь, в случае его истинности, выполняется <оператор> в цикле. Эти действия повторяются до тех пор, пока <условие> не станет ложным. Поскольку параметр цикла используется для управления циклом, необходимо изменять этот параметр внутри составного оператора цикла.

Пример . Вычислить Y = 1+1/2+1/3+...+1/N. Фpагмент пpогpаммы с применением оператора WHILE может быть составлен в следующем виде:

        Y:=0; I:=1;                                                                    

WHILE I<= N DO      

                        begin                                                                                                        Y:=Y+1/I;                                                                                I:=I+1                                                            end; 

                                                                          

5.4. Пример и задания для оператора цикла с предусловием

Пример . Для трех значений а = 0.1, 0.2, 0.3 протабулировать функцию
y = a^.tg(x/4) при изменении аргумента x на интервале [0.5,0.9] с шагом, равным a. Для СА (рис. 9) решения данной задачи программа может быть следующей:

Program a5;

var a, x, y: real; а≤0,3;х=0

Begin

writeln('-------------------------');

writeln(' a | x | y |');

writeln('-------------------------');

a: = 0.1;

while a<=0.31 do

begin

 writeln(a:5:2);

x :=0.5;

while x<=0.91 do                                                                     

begin

y :=a*sin(x/4) / cos(x/4);

writeln(x:12:2,' | ', y:10:2);                                                  

x :=x+a;

 end;

writeln('-------------------------');

a:=a+0.1                                

end;   end .

Задания для самостоятельного выполнения (программа_4_1)

Начертите структурную схему алгоритма, напишите и отладьте про­грамму для табуляции следующих функций:

1. S = ae^-xsin ax+ 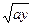                       при -1 <= x <= 1 с шагом 0.2,

      a = 0.75,                                       1 <= y <= 5 с шагом 1.5.

2. Z = 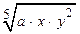+ 1,3 sin(x-a)          при  2 <= x <= 5 с шагом 0.5,

      a = 1.9,                                         -1 <= y <= 1 с шагом 0.5.

3. S = 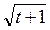e^{2 t y}cos(t-a)                   при 1<= t <= 2 с шагом 0.2,

      a = -2.1,                                        2 <= y <= 3 с шагом 0.3.

4. Z = bx 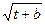(tx+2.1)                     при 1 <= x <= 2 с шагом 0.2,

b = 3.5,                                  0 <= t <= 1 с шагом 0.2.

Z =

 ,                      если 0 <= x <= 2,               a = 0.5; 0.75,

5.                        ,                если 2 < x <= 3.6,          шаг dx = a/2.

        sin ax - 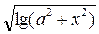,        если 0.1 <= x <= 0.4,

6. Y= a cos²(px),                        если 0.4 < x <= 1.2,   a = 1.0; 1.5,

        2 - sin ax,                         если 1.2 < x <= 1.6,   шаг dx = a/5.

 

7. Z =

Z =

        ln(a+x²/ 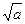) ,                    если 0 <= x <= 2,     a = 1.0; 1.3; 1.6,

         2 e^2x ,                              если 2 < x <= 3.6,    шаг dx = a/4.

 

Z =

        a(e^x+2a+e^-(x-3a),                    если 0.1 <= x < 0.5,

8.     sin x,                                если x = 0.5,              a = 2; 2.1,

    a + a cos(x+3a),               если 0.5 < x <= 1.5,   шаг dx = a/10.

          

9. Z = =

      -a e^x-3a,                              если 0 < x <= 3,         a = 1; 1.5,

        -a(1+ln(x-3a)),                 если 3 < x <= 4,      шаг dx = a/2.

 

        - (x+3a)² - 2a,             если -1 <= x <= 0,

10. Y =  a cos(x+3a) - 3a,             если 0 < x < 1,           a = 0.7; 1,

        a e^x,                                  если x = 1,           dx = (a+0.2)/2.

11. Z =

   a(x-a)^3/2,                           если 1 <= x <= 2.5,    a = 0.5; 1.0,

a/2(e^x/a+e^-x/a),                    если 2.5 < x <= 4,               шаг dx = a/2.

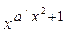        ,                    если 0.5 <= x < 1.5,

 12. Y = a cos x,                            если x = 1.5,              a = 0.1;0.2;0.3;

        (a x² + 1)^x,                        если 1.5 < x <= 3,               шаг dx = 2a.

 

13. Z = Я=Z =

        (sin²x +a)² e^{a sinX} ,             если 0.1 <= x <= 0.5, a = 0.1;0.2;0.3,

        tg(x/4),                             если 0.5 < x <= 0.9,   шаг dx = a.

        tg(a² +sin px),                  если 0 <= x <= 1,

 14.Y =  a sin(p- cos px),         если 1 < x <= 2,       a = 0.5; 0.75; 1;

 lg x,                           если 2 < x < 3,         шаг dx = a/4.

15. Z =

        e^{cos x} -a sin²(px),               если 0.5 <= x <= 1.5 a = 0.1;0.7;1.3,

  a x² - cos px,                    если 1.5 < x <= 2       шаг dx= a/4.

         1/x ,                          если 0.1 <= x <= 0.4

 16. Y =  ln(x²+ ax) ,                если 0.4 < x <= 1.2    a = 1.0; 1.5,

 x² ,                            если 1.2 < x < 1.6     шаг dx = a/5.

17. Дана непустая последовательность различных натуральных чи­сел, за которой следует нуль (признак конца последовательности). Оп­ределить порядковый номер наименьшего из них и его значение.

18. Найти первый отрицательный член последовательности cos (ctg(n)), где n = 1, 2, 3, ..., x . Напечатать его номер и значение. Распечатать всю последовательность.

19. Вычислить наибольший общий делитель (k) натуральных чисел d и f. Оператор FOR не использовать.

20. Задан ряд неотрицательных вещественных чисел. Определить, сколько из них больше своих «соседей»: предыдущего и последующего чисел. Признаком окончания ряда чисел считать появление отрицательно­го числа.