Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Относительно самостоятельные фрагменты программы, оформленные определенным образом и снабженные заголовком, называются подпрограммами. С помощью подпрограмм любая программа может быть разбита на ряд формально независимых друг от друга частей.                   

Подпрограммы делятся на два вида: процедуры и функции. Результа­том исполнения операторов, образующих тело функции, всегда является единственное значение, поэтому ее имя может быть использовано в выра­жениях наряду с переменными и константами.

Если в программе используются процедуры или функции, то их описа­ние должно предшествовать основному блоку программы.

Описание состоит из заголовка и тела процедуры (функции), которое обычно следует за за­головком.

Заголовок процедуры с параметрами описывается строкой

PROCEDURE <имя> (<список формальных параметров> );

Список формальных параметров записывается в скобках и содержит пере­чень параметров с указанием их типов. Перед выходными параметрами, которые воз­вращают результат в основную программу, указывается ключевое слово VAR, например:

PROCEDURE SUMMA(A1,A2:REAL; B1,B2:INTEGER; VAR S1,S2:REAL); Допускаются также процедуры без параметров:

PROCEDURE < имя >;

Они предполагают использование в подпрограмме только глобальных пере­менных, определенных в разделе описаний основной программы.

За заголовком процедуры следует раздел описаний подпрограммы (ме­ток, констант, типов, переменных, а также описаний вложенных процедур и функций) и блок операторов.

Структура описания заголовка подпрограммы-функции имеет вид:

FUNCTION <имя> (<список формальных параметров> ): <тип>;

Формальные параметры записываются с указанием их типа, кроме того, ука­зывается тип самой функции. За заголовком функции следует раздел описаний и блок выполняемых операторов.

Пример

 FUNCTION STEP(x, y : REAL) : REAL;

 VAR a, b : real;

 BEGIN

 ... ...

 END;

После описания блока процедуры или функции следует оператор END, за которым ставится точка с запятой.

Отличие функции от процедуры состоит в том, что функция может возвращать одно значение в основную программу через свое имя, а процедура возвращает несколько значений через список параметров. Поэтому в разделе операторов функции должен быть оператор, который имени функции присваивает значение вида

<имя функции> := <выражение>;

например: STEP := <выражение вещественного типа>.

Вызов подпрограмм производится указанием имени или имени со спис­ком фактических параметров. Фактические параметры не указываются, если в подпрограмме используются только глобальные переменные и в заголовке программы отсутствует список формальных параметров. Если заголовок подпрограммы содержит формальные параметры, то при обращении к подп­рограмме должен обязательно присутствовать список фактических парамет­ров, которые записываются через запятую.

Количество, тип и порядок перечисления фактических параметров должен обязательно соответствовать количеству, типу и порядку перечис­ления формальных параметров в описании подпрограммы.

Структура подпрограммы-функции

Описание блока подпрограммы-функции в общем виде имеет следующую структуру:

    FUNCTION <имя> ( <формальные параметры> ) : <тип>;

{ раздел описаний: переменные, типы, метки}

BEGIN

  { операторы функции }

<имя> :=  <выражение> {имени функции присваивается значение}

END;

Функция передает в вызывающую программу единственное значение, которое хранится под ее именем. В качестве переменных могут использоваться параметры-переменные и параметры-значения. <Тип> функции должен соответствовать значению, которое вычисляется в данной подпрограмме (типу результата). В вызывающую подпрограмму передается значение функ­ции данного типа.

Вызов функции в программе производится не обособленно, как в про­цедуре, а в выражении указывается имя функции со списком параметров.

 

7.4. Примеры и задания с подпрограммой-функцией

Пример 1. Вычислить вторую и N-ю степени числа Х.

PROGRAM FUNC;

VAR X: REAL; N: INTEGER;

FUNCTION STEPEN(M: INTEGER; A: REAL): REAL;

VAR P: REAL;

         I: INTEGER;

         BEGIN

                     P := 1;

                     FOR I :=1 TO M DO P := P*A;

                     STEPEN := P;

         END;

 BEGIN

         READ(X,N);

         WRITELN(' X=', X, ' квадрат', STEPEN(2,X));

         WRITELN(' X=', X, ' степень', STEPEN(N,X));

END.

Пример 2. Даны три массива A (5), B (5), C (5). Найти среднее арифме­тическое значение наименьших элементов массивов.

До написания программы разрабатывается СА главной программы (рис. 14, а) и СА для подпрограммы нахождения наименьшего элемента в любом массиве (рис. 14, б).

Отлаженная программа решения задачи имеет следующий вид:

Program lr8;

type

mass = array[1..5] of integer;

const   a: mass = ( 5,2,7,1,8 ); {заданы массивы констант}

b: mass = ( 3,4,5,6,6 );

c: mass = ( 3,8,5,2,6 );

var n: integer;

sr: real;

FUNCTION minim(d:mass) : integer;      {заголовок функции}

var i, min: integer;

begin    {начало блока операторов функции}

min:=d[1];        

for i:=2 to 5 do

if d[i]<min then min:=d[i];

        writeln('минимальный элемент равен ',min);

      minim := min    {имени функции присваивается значение}

end; {конец блока функции}

BEGIN   {блок основной программы}        

     sr: = (minim(a) + minim(b) + minim(c)) /3; {три обращения к функции}     

writeln(' sr = ', sr:5:2);                                        

END .

Задания для самостоятельного выполнения

Задание 1

Написать и отладить программы для задач из пп. 3.7 и 6.4 с применением подпрограммы-функции с параметрами. Вычисление функции (или обработку массива) выполнить в подпрограмме, а ввод ис­ходных данных и вывод результатов - в основной программе. Предусмот­реть, по крайней мере, два обращения к функции с различными фактичес­кими параметрами.

Для отладки программ использовать средства системы Pascal ABC: пошаговое исполнение программы (трассировку) с контролем значений переменных в окне отладчика.

Задание 2

1. По заданным вещественным массивам A [1..6], B [1..6] и C [1..6] вычислить

        (max B)/max A + (max C)/max(B+C) при min A < max B,

 max(B+C) + max C в противном случае.

2. Даны два двумерных массива целых чисел А [1…5], B [1…5]. Напечатать квадрат того из них, в котором наименьший след (сумма диагональных элементов), считая, что такой массив один.

3. Определить координаты центра тяжести трех материальных точек с массами m₁, m₂, m₃ и координатами (x₁,y₁), (x₂,y₂), (x₃,y₃) по форму­лам

x_c = (m₁x₁+m₂x₂+m₃x₃)/(m₁+m₂+m₃), y_c = (m₁y₁+m₂y₂+m₃y₃)/(m₁+m₂+m₃).

Вычисление координаты оформить функцией с параметрами.

4. Вычислить все медианы для каждого из трех треугольников по заданным в массивах A, B, C сторонам: m_a = 0.5 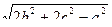, m_b = 0.5 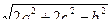, m_c = 0.5 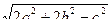. Вычисление медианы оформить функцией.

5. Даны три одномерных массива вещественных чисел A [1..6], B [1..8] и С [1..7]. Найти общую сумму положительных элементов в масси­вах. Нахождение суммы элементов в массиве оформить функцией.

6. Даны два двумерных массива целых чисел с размерами (4х5) эле­ментов. Подсчитать количество отрицательных элементов в каждом из них.

7. Даны два одномерных массива целых чисел A [1..8] и B [1..8]. Найти сумму их максимальных элементов. Для нахождения максимального элемента в массиве использовать функцию.

8. Даны два двумерных массива целых чисел по (5х5) эле­ментов каждый. Подсчитать произведение элементов главных диагоналей в каждом из них.

9. Даны три одномерных массива вещественных чисел A [1..6], B [1..8] и С [1..7]. Найти среднее геометрическое значение положитель­ных элементов для каждого.

10. Даны две матрицы целых чисел M [1..3,0..1], К [1..3,0..2]. Найти среднее арифметическое значение для каждой из них.

11. Даны три одномерных массива целых чисел A [1..6], B [1..8] и С [1..7]. Подсчитать количество неотрицательных элементов в каждом.

12. Даны две матрицы целых чисел S [1..3,0..2], К [1..3,0..2], в каждой из которых имеется по два одинаковых числа. Распечатать их значения.

13. Даны два одномерных массива целых чисел A [1..6] и B [1..8]. Вычислить значение Z = (min A[i] + min B[j]) / min (A[i]+B[j]).

 ^{i            j                    i, j}

14. По заданным целым массивам X[0..7] и Y[8..15] вычислить   

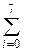x_i² при 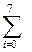x_i y_i+8 > 0,

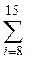        y_i² в противном случае.

15. Дана матрица целых чисел D [1..6,1..5]. Найти наименьшую из сумм неотрицательных элементов строк матрицы. Для вычисления суммы использовать подпрограмму (функцию).

16. Дана матрица целых чисел E [1..3,1..5]. Используя функцию, найти среднее геометрическое значение для каждого столбца матрицы.

17. Дана матрица целых чисел F [1..4,1..5]. Найти наименьшие зна­чения элементов в каждой из строк матрицы с помощью функции.

18. Даны две квадратные вещественные матрицы шестого порядка. Напечатать квадрат той из них, в которой наименьший след (сумма диа­гональных элементов), считая, что такая матрица одна.

19. Сформировать двумерный массив: 1 2 3 4 5

       1 4 9 16 25

       1 8 27 64 125

         ...         …       

Найти правило и оформить функцией вычисление любой строки.

20. Даны две матрицы целых чисел V [1..2,1..3], W [1..3,1..2]. Найти суммы элементов строк и столбцов в этих матрицах.