Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х. Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты. Коэффициент эластичности находится по формуле: 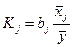, где j- номер факторного признака, если рассматривается множественная регрессия и 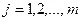, где m – число факторов в модели.

0н показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов. В примере, b=0,19, 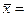507,56 и среднее значение у равно 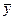=131. Коэффициент эластичности тогда равен 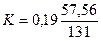=0,58. что говорит о том, что если фактор x изменится на 1%, то фактор y изменится в среднем на 0,58%.

Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных: 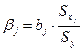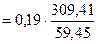=0,99

Т.е. увеличение душевого дохода на величину среднеквадратического отклонения этого показателя  приведет к увеличению среднего значения расходов на питание на 0,99 среднеквадратичного отклонения этих расходов. Это означает, что при увеличении дохода в нашем примере на 309,41 руб., расходы на питание в среднем увеличатся на 58,86 руб. (0,99∙59,45).

Пункты 3 и 4, связаны с темой «Проверка статистических гипотез». Рекомендуется использовать следующую общую процедуру проверки гипотез о значимости коэффициентов регрессии:

Для парной линейной регрессии оценка статистической значимости коэффициента β производится по следующему алгоритму:

1. Выдвигается нулевая гипотеза о том, что коэффициент регрессии статистически незначим: H₀: β =0 на уровне значимости α.

2. Определяется фактическое значение t-критерия для коэффициента регрессии по формуле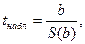  

где S(b) – стандартная ошибка для b; рассчитываемая по формуле

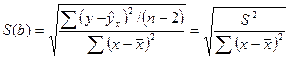, и S² − остаточная дисперсия на одну степень свободы.

Процедура оценивания существенности параметра а не отличается от рассмотренной для коэффициента регрессии b: 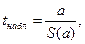где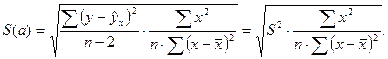

3. Определяется табличное значение t_табл. по таблицам распределения Стьюдента (таблица 1) для заданного уровня значимости a, принимая во внимание, что число степеней свободы для распределения Стьюдента равно (n-2).

4. Если фактическое значение t-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. В противном случае говорят, что нулевая гипотеза отклоняется и на уровне значимости α принимается альтернативная гипотеза о статистической значимости коэффициента уравнения.

В рассматриваемом примере S(b)= 0,013, t_факт.> t_крит., где t_факт. = 14,36 и t_крит.=2,36. Значит, коэффициент существенно отличен от нуля, и зависимость является достоверной.

Проверка значимости линейного коэффициента корреляции r проводится с помощью t -критерия Стьюдента: t_набл. = 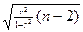сравнивается с критическим значением t-критерия из таблицы значений с учетом заданного уровня значимости (a=0,05) и числа степеней свободы (n-2). Если t_набл.> t_{критич.}, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается). Т.е. делается вывод, что есть статистическая взаимосвязь. В парной линейной регрессии t²_r =F, так как 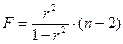. Кроме того, t²_b =F. Следовательно, t²_r = t²_b , и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.

В рассматриваемом примере t²_r = t²_b = 206,20.

Проверка значимости модели регрессии проводится с использованием F- критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели. Если расчетное значение с n₁=(m) и n₂=(n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой:

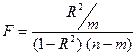, где m – число параметров в модели.

Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:

1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H₀: R²=0 на уровне значимости α.

2. Далее определяют фактическое значение F-критерия по формуле 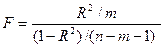, где m=1 для парной регрессии.

3. Табличное значение определяется по таблицам распределения Фишера (табл. 2) для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.

4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу. В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-a) принимается альтернативная гипотеза о статистической значимости уравнения в целом.

В рассматриваемом примере

F_набл..= 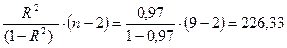, а F_табл.=5,59. Таким образом, F_факт.> F_табл., и принимается гипотеза о статистической значимости уравнения в целом.