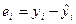Расчет производных величин для определения a и b, а также коэффициента корреляции проведем в таблице следующего вида:
| n | y | x | yx | x2 | y2 | 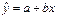
|
| 1 | ||||||
| 2 | ||||||
| 3 | ||||||
| ..... | ||||||
| Сумма | ||||||
| Среднее |
Для определения оценок a и b по известным выборочным данным примера расчетная таблица с результатами будет выглядеть так:
| №
| Расход на питание ( | Душевой доход ( |
|
|
| 1 | 43 | 62 | 2666 | 3844 |
| 2 | 61 | 157 | 9577 | 24649 |
| 3 | 90 | 265 | 23850 | 70225 |
| 4 | 111 | 370 | 41070 | 136900 |
| 5 | 130 | 479 | 62270 | 229441 |
| 6 | 148 | 592 | 87616 | 350464 |
| 7 | 164 | 728 | 119392 | 529984 |
| 8 | 191 | 935 | 178585 | 874225 |
| 9 | 241 | 980 | 236180 | 960400 |
| Сумма |
|
|
|
|
| Среднее |
|
|
|
|
Используя данные таблицы, получим систему нормальных уравнений:
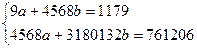
Решением системы будет 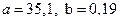 . Таким образом, оценочное уравнение регрессии имеет вид:
. Таким образом, оценочное уравнение регрессии имеет вид:
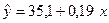
Коэффициентам уравнения линейной регрессии можно придать экономический смысл.
a) Коэффициент 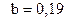 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением дохода на 1 единицу расходы на питание повышаются в среднем на 0,19. Другими словами, из каждого дополнительного рубля дохода в среднем 0,19 копеек будут израсходованы на питание.
показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением дохода на 1 единицу расходы на питание повышаются в среднем на 0,19. Другими словами, из каждого дополнительного рубля дохода в среднем 0,19 копеек будут израсходованы на питание.
в) Коэффициент 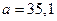 формально показывает прогнозируемый уровень у, но только в том случае, если х =0 находится близко с выборочными значениями. Но если х =0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
формально показывает прогнозируемый уровень у, но только в том случае, если х =0 находится близко с выборочными значениями. Но если х =0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
с) Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя для каждого наблюдения. Полученные величины показывают, какой бы был расход на питание при соответствующих доходах, если бы данная группа n использовала бы свои доходы в такой степени, как в среднем все анализируемые группы.
Результаты необходимо оформить в виде таблицы:
| № п/п | Предсказанное Расход на питание
| Остатки |
| 1 | 46,81 | -3,81 |
| 2 | 64,76 | -3,76 |
| 3 | 85,17 | 4,83 |
| 4 | 105,01 | 5,99 |
| 5 | 125,60 | 4,40 |
| 6 | 146,96 | 1,04 |
| 7 | 172,65 | -8,65 |
| 8 | 211,76 | -20,76 |
| 9 | 220,27 | 20,73 |
| Всего | 1179,00 | 0,00 |
d) Связь между у и х определяет знак коэффициента регрессии b (если >0 – прямая связь, иначе - обратная). В нашем примере связь прямая, т.е. с увеличением душевого дохода расходы на питание также увеличиваются:
Необходимо также построить график полученного уравнения регрессии
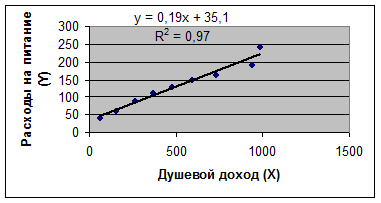
Рис.2. График эмпирического уравнения регрессии
Далее нужно рассчитать показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции 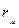 , который рассчитывается по формуле:
, который рассчитывается по формуле:
 ,
,
где 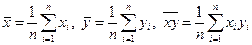 − выборочные средние,
− выборочные средние, 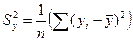 и
и 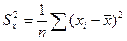 − выборочные дисперсии,
− выборочные дисперсии, 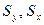 - среднеквадратические отклонения.
- среднеквадратические отклонения.
Линейный коэффициент корреляции принимает значения от –1 до +1. Если 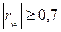 , то связь считается сильной. Если
, то связь считается сильной. Если 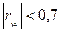 , то связь считается слабой. Этот коэффициент дает объективную оценку лишь при линейной зависимости. В примере
, то связь считается слабой. Этот коэффициент дает объективную оценку лишь при линейной зависимости. В примере 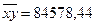 ,
, 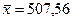 ,
,  ,
, 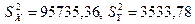 ,
, 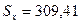 ,
, 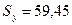 .
.
Тогда выборочный коэффициент корреляции будет равен 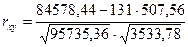 =0,98. Таким образом, линейная связь между расходами на питание и душевым доходом очень тесная.
=0,98. Таким образом, линейная связь между расходами на питание и душевым доходом очень тесная.
Дата: 2019-02-02, просмотров: 639.
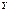 )
)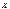 )
)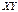
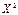
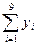 =1179
=1179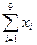 =4568
=4568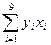 =761206
=761206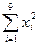 =3180132
=3180132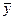 =131
=131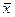 =507,56
=507,56 =84578,44
=84578,44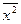 =353348
=353348