МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЭКОНОМЕТРИКА
Программа курса, методические указания для
очно-заочного отделения
Пермь 2018
Составители: доцент, к.ф.-м.н. Н.В.Фролова., к.ф.-м.н. М.В. Радионова
Эконометрика. Программа курса, методические указания
ОБЩИЕ УКАЗАНИЯ
Эконометрика является областью знаний, которая охватывает вопросы применения статистических методов к теоретическим моделям, описывающим реальные экономические процессы.
Эконометрические модели позволяют объяснить те или иные экономические явления или процессы, но, очевидно, они не позволяют получить всю информацию и однозначно определить истинный механизм экономического явления или процесса.
В настоящем пособии даются основные понятия, модели и методы эконометрики, рассматриваются примеры.
Содержание пособия полностью соответствует требованиям государственного стандарта высшего профессионального образования.
Для работы с данным пособием необходимы базовые знания следующих учебных дисциплин: высшая математика, теория вероятностей и математическая статистика, общая и экономическая статистика, экономическая теория.
Объем практических занятий предполагает использование компьютерной техники, как в часы плановых занятий, так и в часы самостоятельной работы.
По курсу Эконометрика студент выполняет одну контрольную работу. Обязательным требованием к ее оформлению является следующее:
1) указать вариант контрольной работы и номер зачетной книжки;
2) при решении каждой задачи необходимо приводить полностью ее условие;
3) решение задачи должно сопровождаться необходимыми формулами, таблицами, графиками, положениями и выводами;
4) при выполнении работы с использованием персонального компьютера следует обязательно указывать название и версию программного обеспечения, которое вы используете;
5) в тексте работы желательно приводить результаты промежуточных расчетов (за исключением работ, расчеты в которых выполнены на персональных компьютерах и сопровождаются распечатками);
6) в конце работы указать список литературы, используемой в решении контрольной работы.
На уровне значимости 0,05 оцените статистическую значимость коэффициента регрессии b и коэффициента корреляции. Сделайте выводы.
Методы исключения тенденции
Сущность всех методов исключения тенденции заключается в том, чтобы устранить или зафиксировать воздействие фактора времени на формирование уровней ряда. Основные методы исключения тенденции можно разделить на 2 группы:
1) методы, основанные на преобразовании уровней исходного ряда в новые переменные, не содержащие тенденции. Полученные переменные используются далее для анализа взаимосвязи изучаемых временных рядов. Эти методы предполагают непосредственное устранение трендовой компоненты Т из каждого уровня временного ряда. Здесь в свою очередь два основных метода:
a. метод последовательных разностей;
b. метод отклонений от трендов.
2) методы, основанные на изучении взаимосвязи исходных уровней временных рядов при элиминировании (исключении) воздействия фактора времени на зависимую переменную и независимые переменные модели. В первую очередь это метод включения в модель регрессии по временным рядам фактора времени.
Пример. Метод последовательных разностей
Основная задача – выявление основной тенденции изучаемого процесса, выраженной неслучайной составляющей f(t) (тренда либо тренда с циклической или (и) сезонной компонентой).
Для определения вида тренда (тенденции) рассчитайте
а) цепные абсолютные приросты d1=Xt-Xt-1;
b) абсолютные ускорения уровней ряда, или вторые разности: d2=dТ-dt-1
c) цепные коэффициенты роста: Kt=Xt-Xt-1 – логарифмы уровней ряда
Проанализируйте полученные результаты:
Ø если приблизительно одинаковые цепные абсолютные приросты, то следует выбрать линейный тренд (Xt=a+bt).
Ø если примерно постоянные абсолютные ускорения уровней ряда, следует выбрать параболу второго порядка (Xt=a+b1t+ b2t2).
Ø если примерно одинаковые цепные коэффициенты роста, моделирование тенденции следует проводить с использованием экспоненциальной кривой (Xt=ea+bt).
Для расчета параметров применить обычный метод МНК (значения t=1,2,3...). В случае нелинейных зависимостей провести линеаризацию исходной функции.
Из двух функций предпочтение отдать той, при которой меньше сумма квадратов отклонений фактических данных от расчетных на основе этих функций. Для выявления основной тенденции чаще всего используется метод наименьших квадратов. Значения временного ряда рассматриваются как зависимая переменная, а время t – как объясняющая: yt=f(t)+et, где et –возмущения, удовлетворяющие основным предпосылкам регрессионного анализа, т.е. представляют независимые и одинаково распределенные случайные величины, распределение которых предполагаем нормальным.
Интерпретация параметров тренда:
В линейном тренде b- это средний за период цепной прирост уровней ряда.
В экспоненциальной функции величина eb- это средний за период цепной темп роста уровней ряда.
Начальный уровень ряда в момент (в период времени) 0 в линейном тренде выражается параметром а, в экспоненциальном тренде – величиной еа.
Автокорреляция в остатках. Критерий Дарбина -Уотсона
Если вид функции тренда выбран неудачно, то вряд ли можно говорить о том, что отклонения от нее (возмущения et) являются независимыми. В этом случае наблюдается заметная концентрация положительных и отрицательных возмущений, и можно предполагать их взаимосвязь. Если последовательные значения коррелируют между собой, то говорят об автокорреляции возмущений (остатков, ошибок).
В случае выявления автокорреляции целесообразно вновь вернуться к проблеме спецификации уравнения регрессии (выбора функции тренда) пересмотреть набор, включенных в него переменных и т.п.
Существует два наиболее распространенных метода определения автокорреляции остатков. Первый метод – это построение графика зависимости остатков от времени и визуальное определение наличия или отсутствия автокорреляции.
Второй метод - наиболее простой и достаточно надежный критерий определения автокорреляции возмущений – критерий Дарбина – Уотсона. С помощью него проверяется гипотеза об отсутствии корреляции между соседними остаточными членами ряда еt и еt-1, где еt - выборочная оценка et. Статистика критерия имеет вид:
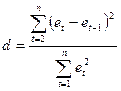 .
.
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий:
1) Выдвигается гипотеза Н0 об отсутствии автокорреляции остатков.
2) По специальным таблицам определяются критические значения критерия dL и dU для заданного числа наблюдений n, числа независимых переменных модели k и уровня значимости a. По этим значениям числовой промежуток [0; 4] разбивают на 5 отрезков:
| Есть положительная автокорреляция остатков. Н0 отклоняется. С вероятностью Р=(1-a) принимается Н1. | Зона неопределенности | Нет оснований отклонять Н0 (автокорреляция остатков отсутствует) | Зона неопределенности | Есть отрицательная автокорреляция остатков. Н0 отклоняется. С вероятностью Р=(1-a) принимается Н1* | ||||||
| 0 | dL | du | 2 | 4-dU | 4-dL |  4 4
| ||||
Статистика d заключена в границах от 0 до 4; при отсутствии автокорреляции d»2; при полной положительной автокорреляции d»0; при полной отрицательной d»4;
Для d-статистики найдены верхняя и нижняя критические границы на уровнях значимости a.=0,01; 0,025; и 0,05.
Если фактически наблюдаемое значение d попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу Н0.
Недостатком критерия является наличие области неопределенности критерия, также методика расчета направлена только на выявление автокорреляции остатков первого порядка, а также то, что критические значения d-статистики определены для объемов выборки не менее 15.
Вопросы к экзамену
1. Основные понятия эконометрики (предмет эконометрики, особенности взаимосвязей экономических переменных, введение случайной компоненты в экономическую модель, понятие эконометрической модели, классификация эконометрических моделей).
2. Этапы построения эконометрической модели. Характеристика первого этапа.
3. Характеристика экономических данных
4. Основные понятия статистического анализа (случайная величина, распределение, основные распределения, числовые характеристики случайных величин.
5. Нормальный закон распределения. Распределение Стьюдента.
6. Статистическое оценивание параметров распределения: определение оценивания параметров распределения, формулировка задачи оценки параметров в общем виде, основные свойства оценок.
7. Метод наименьших квадратов (МНК).
8. Парная линейная регрессия (метод оценивания параметров линейной регрессии, требования к ошибкам ei, свойства оценок.
9. Анализ статистической значимости коэффициентов линейной регрессии.
10. Интерпретация коэффициентов парной линейной регрессии.
11. Анализ остатков. Критерий Дарбина-Уотсона (DW-критерий).
12. Оценка качества модели (коэффициент корреляции, индекс корреляции, коэффициент детерминации).
13. Методика множественного корреляционного анализа: этапы многофакторного корреляционного анализа, отбор факторов.
14. Описание этапа сбора и статистической оценки исходной информации в множественном корреляционном анализе.
15. Спецификация множественной регрессионной модели .(построение системы нормальных уравнений для двухфакторной линейной регрессии). Интерпретация коэффициентов множественной регрессии..
16. Анализ статистической значимости коэффициентов двухфакторной линейной регрессии. Парные и частные коэффициенты корреляции, их интерпретация.
17. Бетта-коэффициенты и коэффициенты эластичности, их назначение и интерпретация.
18. Оценка качества модели множественной регрессии: критерий Фишера. Множественные коэффициенты корреляции и детерминации.
19. Проверка условий, выполнение которых предполагалось при оценивании уравнения регрессии. Автокорреляция остатков. Критерий Дарбина-Уотсона.
20. Временные ряды, их характеристики.
21. Гомоскедастичность и гетероскедастичность. Причины гетероскедастичности. Обнаружение гетероскедастичности.
22. Тест ранговой корреляции Спирмена.
23. Общие сведения о временных рядах: понятие тренда, сезонной компоненты, циклической компоненты. Основные этапы анализа временных рядов.
24. Определение вида тренда. Расчет параметров тренда. Интерпретация параметров тренда.
25. Основные понятия системы одновременных уравнений. Проблема идентификации.
26. Методы расчета структурных параметров системы.
27. Экономическое прогнозирование на основе построенной модели.
28. Понятие ошибок при построении доверительного интервала.
Литература
Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики. М.: ЮНИТИ,1998.
Доугерти К. Введение в эконометрику. М.: МГУ,1999.
Канторович Г.Г. Эконометрика //Методические материалы по экономическим дисциплинам для преподавателей средних школ и вузов. Экономическая статистика. Эконометрика. Программы, тесты, задачи, решения /Под ред. Л.С.Гребнева. М.: ГУ-ВШЭ, 2000.
Кремер Н.Ш., Путко Б.А. Эконометрика. М.:ЮНИТИ-ДАНА, 2002.
Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. М.: Дело, 1999.
Катышев П.К., Магнус Я.Р., Пересецкий А.А. Сборник задач к начальному курсу эконометрики. М.: Дело, 2002.
Практикум по эконометрике /Под ред. Н.И. Елисеевой. М.: Финансы и статистика, 2001.
Эконометрика /Под ред. Н.И. Елисеевой. М.: Финансы и статистика, 2001.
Экономико-математические методы и прикладные модели /Под ред. В.В. Федосеева. –М.: ЮНИТИ,1999.
О.О. Замков, Черемных Ю.А., Толстопятенко А.В. Математические методы в экономике. –М.: Дело и Сервис,1999.
Мардас А.Н. Эконометрика. –СПб.: Питер, 2001.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
ЭКОНОМЕТРИКА
Программа курса, методические указания для
очно-заочного отделения
Пермь 2018
Составители: доцент, к.ф.-м.н. Н.В.Фролова., к.ф.-м.н. М.В. Радионова
Дата: 2019-02-02, просмотров: 643.