При проведении количественного анализа обычно измеряют или определяют расчетным путем на основании проведенных измерений различные физические величины: массу вещества, концентрацию раствора, объем жидкости, интенсивность окраски вещества, оптическую плотность среды, окислительно-восстановительные потенциалы, показатели преломления света и другие аналитические сигналы.

Все без исключения физические величины измеряются с некоторой ошибкой (погрешностью). Невозможно измерить какую-либо физическую величину точно (да и сам термин «точно» неясен и должен быть конкретно определен). Поэтому при проведении количественного анализа и соответствующих расчетов необходимо в количественной форме (численно) учесть ошибки определения.

Источники ошибок могут быть самыми разнооброазными.

Если при проведении количественного анализа допущены существенные отступления от методики или явные ее нарушения, то анализ необходимо повторить заново, отбросив явно неправильные результаты.

Повторить некорректно проведенный анализ — это непременное
правило.

Однако даже если строго соблюдены все требования, предусмотрен­ные методикой, результаты отдельных независимых анализов одного и того же объекта все равно, как правило, несколько различаются. Эти различия целесообразно оценить количественно, чтобы понять, насколько достоверны найденные результаты. Подобная оценка обычно подразумевает получение метрологических характеристик на основе положений теории вероятности (теории ошибок). При этом полезно помнить, что любая статистическая обработка данных эксперимента является при­ближенной, имеет вероятностный смысл.

Правильность и воспроизводимость результатов количественного анализа

Для выявления ошибок и их численной оценки (особенно при разра­ботке новых аналитических методик) количественный анализ повторяют несколько раз, т. е. проводят параллельные определения. Под параллельными определениями понимают получение нескольких результатов единичных определений для одной пробы практически в одинаковых условиях.

Пусть μ — истинное значение определяемой величины; х₁, х₂, …, х_i, …, …, x_n -  измеренные (единичные) значения определяемой величины — результаты единичных определений; п  общее число единичных определений.

Под единичным определением понимают однократное проведение всей последовательности операций, предусмотренных методикой анализа.

Результат единичного определения — это значение содержания оп­ределяемого компонента, найденное при единичном определении.

Иногда (часто) вместо истинного значения определяемой величины ц используют действительное значение содержания а (или просто действительное значение а), под которым подразумевают экспериментально полученное или расчетное значение определяемого содержания, настолько близкое к истинному, что для данной цели может быть использовано вместо него.

Тогда величина

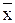=(х₁+х₂+... + х _n )/п = (Σ x _n )/ n                            (1)

есть среднее арифметическое (среднее) из результатов единичных определений. Считается, что 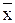 — наиболее вероятное значение определяе­мой величины, более вероятное, чем каждое отдельное значение x_i.

Под правильностью результата анализа понимают качество анализа, отражающее близость к нулю разности между средним арифметическим и истинным μ (или действительным а) значением определяемой величины:

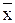 - μ → 0  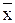     - α → 0  

или

при n → ∞     при n → ∞

Другими словами, правильность результата анализа отражает бли­зость полученного среднего значения 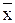 к истинному (или действитель­ному) значению определяемой величины.

Воспроизводимость результата анализа характеризует степень бли­зости результатов единичных определений х _i друг к другу.

Правильность и воспроизводимость результата анализа зависят от различного типа ошибок.