Цель работы: Изучить понятия частотных характеристик и методики их практического снятия.
Теоретические сведения
Частотные характеристики – это один из методов теоретического исследования свойств замкнутых систем регулирования. Метод предполагает исследование реакции системы (или звена) на гармоническое (синусоидальное) входное воздействие. Предполагается, что входное воздействие меняется по синусоидальному закону, при этом выходная переменная для линейных систем имеет также синусоидальный характер, но выходная синусоида, как правило, сдвинута по фазе относительно синусоиды входного воздействия. Частота входного воздействия теоретически изменяется от нуля до бесконечности. Выходная переменная будет иметь ту же частоту, что и входная, но на разных частотах будут различны её амплитуда и фазовый сдвиг относительно входного сигнала. Законы изменения амплитуды и фазового сдвига выходной переменной при изменении частоты и есть частотные характеристики. На практике оценивают изменение не самой амплитуды выходной переменной, а изменение усиления амплитуды при изменении частоты. Усилением амплитуды называется отношение амплитуды выходного сигнала к амплитуде входного воздействия:
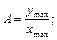 (5.1)
(5.1)
где ymax – амплитуда выходного сигнала (см. рисунок 5.1);
xmax – амплитуда входного сигнала.
Фазовый сдвиг φ (в радианах или угловых градусах) определяется, как это показано на рисунке 5.1.
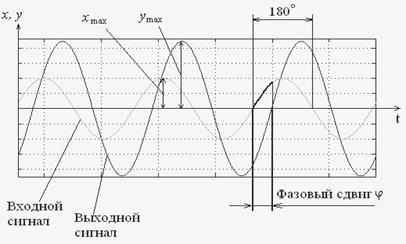
Рисунок 5.1 – К определению усиления амплитуды и
фазового сдвига
График зависимости усиления амплитуды от частоты А(ω) называется амплитудной частотной характеристикой (АЧХ), а график зависимости фазового сдвига от частоты φ(ω) – фазовой частотной характеристикой (ФЧХ). Пример АЧХ и ФЧХ приведён на рисунке 5.2.

Рисунок 5.2 – Пример частотных характеристик
Практически частотные характеристики снимаются следующим образом:
1) На вход исследуемого звена (системы) подаётся синусоидальный сигнал определённой частоты и амплитуды, при этом выходной сигнал будет также синусоидальным;
2) По (5.1) вычисляется усиление амплитуды и графически определяется фазовый сдвиг для заданной частоты входного воздействия;
3) Полученное значение усиления амплитуды при заданной частоте откладывается на координатной плоскости А(ω), а значение фазового сдвига – на координатной плоскости φ(ω);
4) Изменяется частота входного воздействия (обычно без изменения его амплитуды) и проделывается то же самое;
5) И так – для ряда значений частоты ω (теоретически – до бесконечности).
Задание №1. Снять АЧХ и ФЧХ пропорционального звена первого порядка.
Для снятия частотных характеристик целесообразно воспользоваться моделью, приведённой на рисунке 5.3. На экране осциллографа в этом случае будут отображены осциллограммы (входного воздействия и выходной переменной). Параметры исследуемого звена задаются преподавателем.
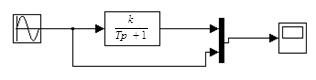
Рисунок 5.3 – Структурная схема для снятия частотных характеристик
1) Задаваясь различными значениями круговой частоты ω входного сигнала, определить соответствующие этим частотам усиление амплитуды и фазового сдвига. Вычисленные значения занести в таблицу (по типу таблицы 5.1).
Таблица 5.1 – К построению частотных характеристик
| ω , с-1 | 0 | 0,1 | 0,3 | 1 |
|
|
|
|
|
| ∞ |
| А |
|
|
|
|
|
|
|
|
|
|
|
| φ, град. |
Обратите внимание, что:
при изменении частоты входного сигнала (блок Sine Wave) схему нужно запускать на решение заново;
отставание выходного сигнала по фазе от входного означает, что фазовый сдвиг отрицательный;
фазовый сдвиг можно отследить только на третьем или на последующих колебаниях, так как на первом колебании MATLAB не показывает отставание по фазе (график всегда строится из 0, то есть на первом колебании нельзя увидеть фазовый сдвиг).
2) Построить графики частотных характеристик (как правило, фазовая характеристика строится непосредственно под амплитудной, причём масштаб осей ω для обоих графиков одинаков);
3) Сделать выводы, в каких диапазонах при изменении ω от 0 до ∞ изменяются усиление амплитуды и фазовый сдвиг пропорционального звена первого порядка.
Задание №2. По аналогии с заданием №1 снять АЧХ и ФЧХ реального интегрирующего звена.
Отчёт по работе должен содержать схемы моделирования, заполненные таблицы и графики снятых частотных характеристик и выводы.
Частотные характеристики могут представляться не только в виде АЧХ и ФЧХ, но и в других видах, что бывает удобно для анализа и синтеза САР. В частности, вместо двух названных характеристик на комплексной плоскости может построена одна амплитудно-фазовая частотная характеристика (АФЧХ), или эти характеристики могут быть построены в логарифмических масштабах (логарифмическая амплитудная характеристика – ЛАХ, и логарифмическая фазовая характеристика – ЛФХ). Эти характеристики, как правило, получаются соответствующим пересчётом исходных АЧХ и ФЧХ. Методика построения АФЧХ, ЛАХ и ЛФХ приведена в любом учебнике по теории автоматического управления.
Задание №3. Построить ЛАХ и ЛФХ звеньев и цепочек звеньев, заданных преподавателем. Построенные характеристики (с необходимыми расчётами) привести в отчёте по лабораторной работе.
В Matlab для анализа систем автоматического управления может использоваться специальный инструмент LTI Viewer (обозреватель LTI-объектов). В этом разделе автоматически строятся переходная характеристика, АЧХ, ФЧХ, ЛАХ, ЛФХ, АФЧХ.
С инструментом LTI Viewer можно познакомиться, открыв в модельном окне:
Tools → Linear Analisys.
При выборе данного инструмента откроется окно с 2 элементами (рисунок 5.4) – а точкой входа (Input Point) и точкой выхода (Output Point):

Рисунок 5.4 – Сигналы Model Inputs and Outputs
Точку входа и точку выхода помещают в необходимых местах структурной схемы в модельном окне, при этом открывается окно LTI Viewer: untitled, в котором и отображаются основные характеристики. Точки Input Point и Output Point устанавливают в структурной схеме таким образом, чтобы выделить тот фрагмент схемы, характеристики которого необходимо получить. Например, если необходимы характеристики всей замкнутой системы, точку Input Point помещают на вход структурной схемы, а точку Output Point – на выход. При этом откроется окно характеристик LTI Viewer: untitled, в котором будут представляться необходимые характеристики (рисунок 5.5). Запускается программа в меню Simulink этого окна командой Get linearized model.
При нажатии правой кнопкой мыши на поле диаграммы откроется меню, изображенное на рисунке 5.5.
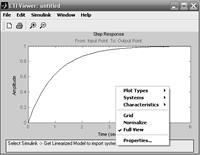
Рисунок 5.5 – Окно LTI Viewer: untitled
В данном меню можно выбрать тип характеристики системы, используя раздел Plot Types (тип графика):
- Step – переходная характеристика;
- Impulse – весовая характеристика;
- Bode – ЛАХ и ЛФХ;
- Bode Magnitude – ЛАХ;
- Nyquist - диаграмма Найквиста.
В этом же меню в разделе Characteristics (характеристики) можно определить некоторые свойства системы, например:
- Setting Time – время переходного процесса;
- Peak Response – перерегулирование;
- Stability (Minimum Crossing) – устойчивость системы.
При помощи инструмента LTI Viewer автоматически выполняется проверка устойчивости системы по характеристикам Bode. Для этого необходимо в разделе Characteristics выбрать свойство Stability (Minimum Crossing). На графике появятся характерные точки (рисунок 5.6). При подводе курсора к точке всплывает подсказка со сведениями о системе (Phase Margin (deg) – фазовый сдвиг в градусах; Delay Margin – величина задержки, показывающая запас по времени до потери устойчивости; At frequency – частота, на которой произошла потеря устойчивости; Closed Loop Stable? – устойчива (Yes) или неустойчива (No).
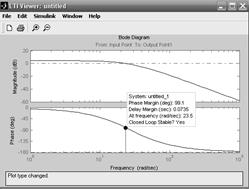
Рисунок 5.6 – ЛАХ и ЛФХ системы
Задание №4. С использованием инструмента Tools построить ЛАХ и ЛФХ систем, заданных преподавателем, и проверить их на устойчивость.
Лабораторная работа №6.
Дата: 2019-02-02, просмотров: 360.