Передаточная функция пропорционального безынерционного звена имеет вид 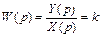, пропорционального звена первого порядка – 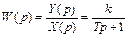, а пропорционального звена второго порядка – .

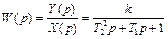В этих выражениях k – передаточный коэффициент, T_i – постоянные времени.

Задание №1. Определить параметры пропорционального звена первого порядка.

1) Снять переходную характеристику звена, заданного преподавателем;

2) По полученному переходному процессу определить передаточный коэффициент и постоянную времени звена (округлить до первого знака после запятой);

3) Записать передаточную функцию пропорционального звена первого порядка с полученными численными значениями параметров;

4) Для проверки построить переходной процесс звена, выбранного из библиотеки Simulink, с параметрами, равными полученным в эксперименте;

5) В отчёт внести исходную схему моделирования, полученную переходную характеристику с построениями, необходимыми для расчёта параметров звена, и выражение передаточной функции.

Задание №2. Определить влияние параметров звена на его статические и динамические свойства.

В качестве схемы моделирования используйте схему по пункту 4 предыдущего задания.

1) Снимите переходные характеристики звена при двух разных конечных значениях входного воздействия. Зарисуйте осциллограммы (в одной координатной системе);

2) Снимите переходные характеристики звена при двух разных значениях передаточного коэффициента. Зарисуйте осциллограммы;

3) Снимите переходные характеристики звена при двух разных значениях постоянной времени. Зарисуйте осциллограммы;

4) По полученным осциллограммам оцените, как выше перечисленные параметры влияют на величину установившегося значения выходной величины и на длительность переходного процесса;

5) В отчёт внести полученные осциллограммы (рисунки с осциллограммами по п.п. 1 – 3 не совмещать!) и выводы.

Передаточная функция пропорционального звена второго порядка имеет вид

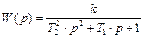
или

,

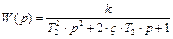где 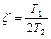 – коэффициент демпфирования.

Величина коэффициента демпфирования, то есть соотношение постоянных времени при первой и второй производных, определяет вид переходного процесса. При ζ ≥ 1 (Т₁ ≥ 2Т₂) переходной процесс получается апериодическим (звено в этом случае называется апериодическим второго порядка). При ζ < 1 (Т₁ < 2Т₂) переходная характеристика имеет вид затухающих колебаний (звено в этом случае называется колебательным). При ζ = 0 (Т₁ = 0) переходной процесс получается в виде незатухающих колебаний (звено – консервативное).

Задание №3. Определить влияние коэффициента демпфирования на вид переходных характеристик пропорционального звена второго порядка.

1) Снять переходные характеристики пропорционального звена второго порядка с k = 2 и Т₂ = 1 с при значениях коэффициента демпфирования, равных 2; 1; 0,5; 0,1; 0. Зарисовать осциллограммы в отчёте;

2) Сделать выводы, как уменьшение коэффициента демпфирования влияет на качество переходного процесса, на его длительность, амплитуду и частоту колебаний (для колебательного звена).

Апериодическое звено второго порядка может быть представлено как два последовательно соединённых пропорциональных звена первого порядка, то есть, его передаточную функцию

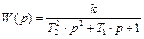
можно записать как

,

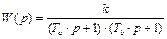где Т_а, Т _b могут быть найдены из равенства знаменателей обеих форм записи:

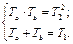
Как правило, по переходной характеристике проще определить постоянные времени Т_а и Т _b. Для этой цели в литературе предлагается несколько методик. Одна из методик приведена ниже.

Задание №4. Определить постоянные времени апериодического пропорционального звена второго порядка по его экспериментально снятой переходной характеристике.

1) Снять переходную характеристику звена с передаточной функцией

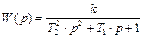
при заданных преподавателем значениях постоянных времени Т₁ и Т₂          (k – произвольно);

2) По полученной осциллограмме определить постоянные времени Т_а и Т _b звена. Постоянные времени определить по предложенной ниже или любой другой методике.

Методика определения постоянных времени апериодического звена второго порядка.

а) по переходной характеристике (рисунок 3.1) при значении выходной величины, равной 0,73y_уст, определяется величина t_р, равная 1,3(Т_а + Т _b):

t_р = 1,3∙(Т_а + Т _b),                                        (3.1)

где Т_а , Т _b – искомые постоянные времени;

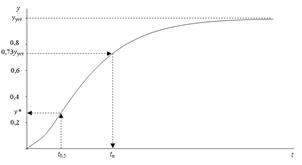
Рисунок 3.1 – Переходная характеристика апериодического

звена 2 порядка

б) вычисляется значение t_0,5, при котором

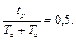                                          (3.2)

Для этого достаточно правую и левую части (3.1) разделить на 2,6, то есть ;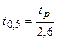

в) по переходной характеристике определяется относительное значение выходной величины y*, соответствующее вычисленному t_0,5 (оно не меньше 0,26 и не больше 0,4);

г) по кривой, приведённой на рисунке 3.2, для найденного значения y* определяется величина ;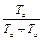

д) По найденному значению 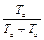 и формуле (3.1) вычисляются значения Т_а и Т_b (с точностью до первого знака после запятой).

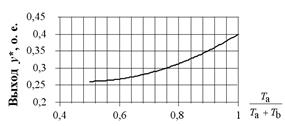
Рисунок 3.2 – К определению постоянных времени

3) Снять переходную характеристику двух последовательно включённых пропорциональных звеньев первого порядка (рисунок 3.3) с расчётными значениями Т_а и Т _b. Сравнить полученную переходную характеристику с характеристикой, снятой в пункте 1.

Рисунок 3.3 – Модель для проверки расчётов

В отчёт должны быть занесены: исходная модель, кривая переходного процесса, рассчитанные значения постоянных времени.

По экспериментально снятой переходной характеристике можно также определить и параметры колебательного звена (передаточный коэффициент, постоянную времени, коэффициент демпфирования). Методика определения параметров приведена в [1].

Задание №5. Определить постоянную времени и коэффициент демпфирования колебательного звена по его экспериментально снятой переходной характеристике.

1) Снять переходную характеристику звена с передаточной функцией

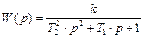
при заданных преподавателем значениях постоянных времени Т₁ и Т₂          (k – произвольно);

2) По полученной осциллограмме определить постоянные времени Т₂ и коэффициент демпфирования ζ звена, пользуясь методикой, изложенной в [1];

3) Сравнить полученные значения Т₂ и ζ с вычисленными по заданным параметрам.

В отчёт занести: исходную передаточную функцию, кривую переходного процесса, графические построения, необходимые для определения параметров звена, значения полученных параметров.