в прикладной программе Simulink

Цель работы: Изучить понятия статической и динамической характеристик звена и методик их снятия, а также получение основополагающих сведений о параметрах, характеризующих статические и динамические свойства звеньев.

Теоретические сведения

Для математического описания процессов в системе автоматического регулирования (САР) необходимо для каждого элемента составить уравнение, связывающее входную и выходную переменные. Совокупность всех уравнений представляет собой математическую модель САР. Звено структурной схемы САР – это графическое представление уравнения, связывающее входную и выходную переменные (рисунок 2.1)

Рисунок 2.1 – Звено структурной схемы:

Х(p) – входная переменная; Y(p) – выходная переменная

Статическая характеристика звена – это зависимость выходной величины от входной в статических (установившихся) режимах. Для снятия статической характеристики необходимо задаться рядом значений входного воздействия и измерить соответствующие им значения выходной величины (выходная величина измеряется по окончанию переходных процессов). Графическое представление зависимости выходной величины от входной и есть статическая характеристика.

Как правило, статические характеристики (как и вообще уравнения, описывающие звенья) в той или иной мере нелинейны. Если нелинейность несущественна, уравнения (характеристики) линеаризуют, чтобы для анализа и синтеза свойств САР использовать аппарат линейных систем. Линеаризация уравнений обычно осуществляется разложением в ряд Тейлора и отбрасыванием малостей высокого порядка. Статические характеристики могут быть линеаризованы и графически, как это показано на рисунке 2.2. Для этого к характеристике в точке рабочего режима проводится касательная, которая принимается в качестве новой (теперь – линейной) характеристики. В качестве переменных в этом случае принимаются не сами входная и выходная величины, а их отклонения (приращения) ∆Х и ∆Y.

По линеаризованной статической характеристике определяется важнейший показатель статики звена – передаточный коэффициент. Он определяется как отношение приращения выходной величины к приращению входной в статическом режиме:

.

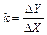Принцип определения передаточного коэффициента по статической характеристике пояснён на рисунке 2.2.

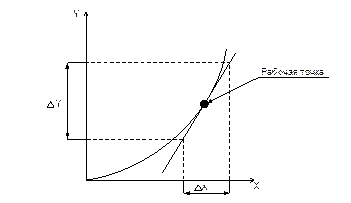
Рисунок 2.2 – К определению передаточного коэффициента

Задание № 1. Снять статическую характеристику звена и определить его передаточный коэффициент.

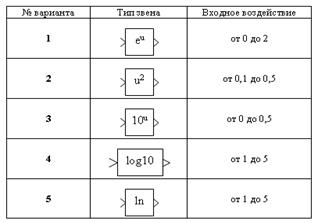
1) Вариант задания задаётся преподавателем (варианты приведены в таблице 2.1).

2) Построить экспериментально статическую характеристику звена:

- собрать структурную схему в модельном окне в соответствии с заданным вариантом (рисунок 2.3);

- составить таблицу из 5-6 значений входной и выходной величин;

- изменяя на входе (Constant) звена сигнал в заданном диапазоне (5-6 точек), измерить выходной сигнал (Display) после окончания переходных процессов и сделать соответствующие записи в таблице;

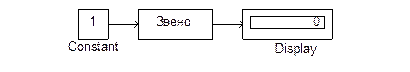
Рисунок 2.3 – Структурная схема

- построить по полученным значениям в масштабе статическую характеристику звена.

Определить передаточный коэффициент звена в точке характеристики, заданной преподавателем.

Таблица 2.1 – Варианты к заданию №1

Динамические характеристики показывают характер изменения выходной величины во времени при изменении входного воздействия (переходной процесс). Одним из видов динамической характеристики является переходная характеристика – реакция звена (или системы) на единичное ступенчатое воздействие. Возможный вид переходной характеристики приведён на рисунке 2.4. По кривой переходного процесса определяются основные динамические (и статические) свойства систем:

· устойчивость – способность системы принимать прежнее или новое установившееся состояние после окончания переходных процессов;

· колебательность системы;

· перерегулирование, оценивающее максимальное отклонение выходной величины от установившегося значения:

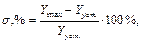
где Y_max – максимальное отклонение выходной величины;

Y_уст – установившееся значение выходной величины;

· число и период ( 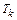) колебаний;

· время переходного процесса t_п и ряд других.

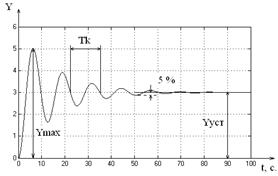
Рисунок 2.4 – Динамическая характеристика

Если входным воздействием являлось возмущающее воздействие в системе, то величина Y_уст характеризует величину статической ошибки системы. По установившемуся значению выходной величины можно также определить передаточный коэффициент звена, который равен 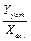, где Х_вх – величина входного воздействия.

Задание № 2. Снять переходную характеристику звена по структурной схеме, приведённой на рисунке 2.5 (численные значения коэффициента и постоянных времени могут быть заданы преподавателем).

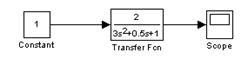
Рисунок 2.5 – Структурная схема

1) промоделировать систему и открыть окно осциллографа с графиком переходного процесса (осциллограмму не зарисовывать);

2) повторить опыт, задав время моделирования от 0 до 100 с (в закладке Simulation parameters меню Simulation).

Обратите внимание, что график переходного процесса получается не «гладкий», а в виде ломаной линии. Это говорит о том, что Matlab по умолчанию установил достаточно большой шаг интегрирования. Исправить этот недостаток можно также в закладке Simulation parameters, выбрав в строках Solver options один из известных способов интегрирования с постоянным или переменным шагом, и задав шаг интегрирования в строках Max step size и Min step size. В данном случае можно задать Max step size, равным 0.01, а  Min step size, равным 0.001.

3) повторить опыт при новых параметрах интегрирования.

Обратите внимание, что график переходного процесса в окне Scope отображается только в промежутке времени от 50 до 100 с, а не от 0 до 100 с, как это было задано в параметрах интегрирования. Это можно исключить, если в параметрах осциллографа (Scope parameters) в закладке (Data history) увеличить число запоминаемых осциллографом точек (строка Limit data points to last) или убрать «галочку» в Limit data points to last (рисунок 2.6).

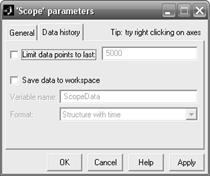
Рисунок 2.6 – Окно Scope parameters

4) задать оптимальное, по Вашему мнению, время моделирования, снять переходную характеристику и зарисовать график переходного процесса. По полученной осциллограмме определить:

· передаточный коэффициент звена;

· ориентировочное время переходного процесса;

· величину перерегулирования в процентах;

· число и период колебаний за время переходного процесса.

Задание № 3. Снять переходные характеристики звеньев, заданных преподавателем, и определить те же параметры, что и в задании №2.

Отчёт по лабораторной работе должен содержать:

· цель работы;

· схемы исследуемых моделей;

· снятые статические и динамические характеристики;

· расчёты статических и динамических показателей;

· выводы по работе.

Лабораторная работа № 3