Некоторые представления о точности эксперимента и об адекватности математической модели может дать построение соответствующих графиков. Графики следует строить по расчетным значениям функции отклика. При этом единичные большие отклонения экспериментальных точек от расчетных кривых будут свидетельствовать о грубых ошибках эксперимента, а большой разброс экспериментальных точек относительно расчетных – о том, что принятая математическая модель неадекватна эксперименту.
С увеличением числа факторов преимущества графического представления эксперимента исчезают. Поэтому в теории эксперимента для оценки точности эксперимента и адекватности математической модели эксперименту применяются статистические методы. Эти методы позволяют оценить надежность и точность выводов, делаемых на основании ограниченного статистического материала. Ниже рассматривается одна из известных методик оценки точности эксперимента и адекватности математической модели эксперименту.
Расчет среднего значения функции отклика
,
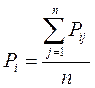где i – номер независимого опыта в плане эксперимента, (i = 1…N); N – количество независимых опытов плана; j – номер параллельного опыта, j = 1…n; n – количество параллельных опытов.
Дисперсии Si2 вычисляются
,
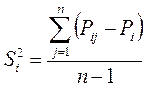где n – 1 = f – число степеней свободы, равное числу «лишних» опытов.
Проверка однородности дисперсии независимых опытов
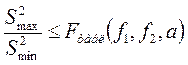, (9)
где S2max, S2min – максимальная и минимальная дисперсии.
Значение критерия Фишера выбирается по табл. 2 в зависимости от числа степеней свободы числителя f1 и знаменателя f2 и уровня статистической значимости a. Критерий Фишера при 5-процентном уровне значимости.
Таблица 2
| f1 f2 | 1 | 2 | 3 | 4 | 5 | 6 | 12 | |||
| 1 | 164.4 | 199.5 | 215.7 | 224.6 | 230.2 | 234 | 245 | |||
| 2 | 18.5 | 19.2 | 19.2 | 19.3 | 19.3 | 19.4 | 19.4 | |||
| 3 | 10.1 | 9.6 | 9.3 | 9.1 | 9.0 | 8.9 | 8.7 | |||
| 4 | 7.7 | 6.9 | 6.6 | 6.4 | 6.3 | 6.2 | 5.9 | |||
| 5 | 6.6 | 5.8 | 5.4 | 5.2 | 5.1 | 5.0 | 4.7 | |||
| 6 | 6.0 | 5.1 | 4.8 | 4.5 | 4.4 | 4.3 | 4.0 | |||
| 12 | 4.8 | 3.9 | 3.5 | 3.3 | 3.1 | 3.0 | 2.7 | |||
Если условие (9) выполняется, то дисперсии однородны, т.е. все измеренные значения являются случайными величинами и подчиняются закону нормального распределения. Опыты с неоднородными дисперсиями не учитываются при вычислении дисперсии эксперимента (отбрасывается или наибольшая, или наименьшая дисперсия; затем проверка однородности дисперсии повторяется).
По однородным дисперсиям вычисляется дисперсия эксперимента
,
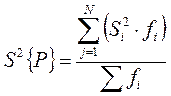где Si2 – дисперсия в i-м опыте; fi – число степеней свободы в i-м опыте; N – число независимых опытов (N = 4); ∑ fi – число степеней свободы эксперимента (∑ fi = 12).
Расчет среднего квадратичного отклонения S { P }
.
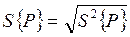Определение доверительного интервала Δ
,
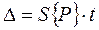где t – критерий Стьюдента, зависящий от числа степеней свободы эксперимента (∑ fi) и уровня статистической значимости a; выбирается по табл. 3.
Таблица 3
| f | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| t | 12.7 | 4.3 | 3.2 | 2.8 | 2.6 | 2.45 | 2.37 | 2.31 | 2.26 | 2.23 | 2.2 | 2.18 |
Оцениваются грубые опыты
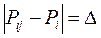. (10)
Если условие (10) выполняется, то опыт считается грубым (выходит за доверительный интервал), а если не выполняется, то грубых опытов нет.
Дата: 2019-02-02, просмотров: 235.
