Технологическими составляющими силы резания называют ее проекции на технологические оси x , y , z:
– ось x направлена вдоль подачи S;
– ось y перпендикулярна к обработанной поверхности;
– ось z совпадает с вектором V скорости главного движения.
Ось ν расположена в горизонтальной плоскости и совпадает с направлением схода стружки.
На рис. 1 показаны составляющие силы резания, действующие на резец. Равные им, но противоположно направленные составляющие действуют на заготовку.
В плоскости, проходящей через оси ν и z расположена суммарная равнодействующая сила резания P. Точка О – точка приложения этой силы. Проекцию силы P на оси x , y , z и ν обозначают соответственно Px , Py , Pz и Pν.
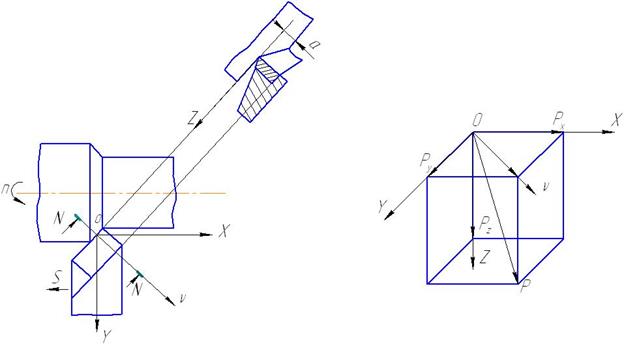
а) б)
Рис. 1. Составляющие силы резания: технологические оси (а); схема составляющих силы резания (б)
Сила – есть вектор ν. Вектор определяется модулем силы P и направлением.
Из рис. 1 следует:
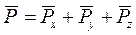 ;
; 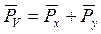 . (1)
. (1)
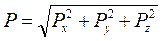 ;
; 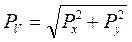 . (2)
. (2)
Силу Px называют силой подачи. Она используется при проектировании механизма подачи станка.
Силу Py называют радиальной силой. Она деформирует заготовку, оказывает большое влияние на точность и виброустойчивость обработки.
Силу Pz, вертикальную составляющую силы резания, часто называют главной составляющей силы резания. Эта сила вместе со скоростью резания определяет мощность резания (эффективная мощность), а вместе с диаметром заготовки – крутящий момент на валу шпинделя станка.
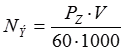 или
или 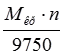 ,
, 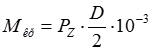 , (3)
, (3)
где Pz – вертикальная составляющая силы, Н; V – скорость резания, м/мин, N э – мощность резания, кВт; D – диаметр обработки, мм; Мкр – крутящий момент резания, Н·м; n – частота вращения шпинделя (заготовки), об/мин.
При прямых срезах (t > S) имеют место следующие средние соотношения между составляющими силы резания
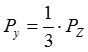 ,
, 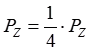 . (4)
. (4)
Подставляя (4) в (2), получим:
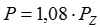 или
или 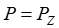 . (5)
. (5)
Таким образом, сила Pz по модулю практически равна равнодействующей силе P. Поэтому силу Pz называют главной составляющей силы резания.
Методика планирования многофакторного эксперимента и обработка опытных данных
Зависимость главной составляющей силы резания от режимов резания с достаточной точностью можно аппроксимировать степенной моделью вида
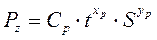 , (6)
, (6)
где Ср, x р , y р – коэффициенты математической модели. Эти коэффициенты определяются экспериментально.
В результате проведения эксперимента необходимо получить некоторое представление о виде отклика, которую в общем случае можно аналитически описать функцией: P = f(t , S), где P – исследуемая функция; t и S – независимые переменные.
В теории эксперимента независимые переменные (t , S) принято называть факторами, а зависимую переменную P – функцией отклика. Значения, которые принимают факторы, называются уровнями. Для определения коэффициентов математической модели Ср, xp , yp используют план эксперимента, в котором каждый фактор варьируется на двух уровнях – нижнем и верхнем. Наименование значения факторов будем называть нижнем уровнем t в и S в. Нижние и верхние уровни факторов ограничивают область определения функции отклика Р. Число опытов полного факторного эксперимента N = р k, где р – число уровней; k – число факторов. В нашем случае план эксперимента для двух факторов и двух уровней будет состоять из 4 опытов (N = 22 = 4).
Обработка результатов опытов упрощается, если от значений факторов в натуральном масштабе перейти к нормированным переменным, которые принимают значения -1, если фактор находиться на нижнем уровне, и +1, если фактор находится на верхнем уровне.
План эксперимента с использованием нормированных переменных Х1 и Х2 может быть представлен следующей таблицей, или матрицей (табл.). Для повышения точности математической модели каждый опыт повторяется несколько раз.
Таблица
| № опыта | Х1 | Х2 | P |
| 1 | -1 | -1 | P1 |
| 2 | +1 | -1 | P2 |
| 3 | -1 | +1 | P3 |
| 4 | +1 | +1 | P4 |
С целью приведения модели к линейному виду необходимо перейти к новым переменным (к логарифмам переменных). Для этого прологарифмируем равенство (6) и получим
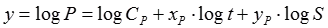 . (7)
. (7)
Коэффициенты математической модели Ср, хр, y р вычисляют с использованием метода наименьших квадратов из условия минимума суммы квадратов разностей между расчетными и экспериментальными значениями функции отклика
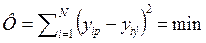 .
.
Необходимые условия минимума функции запишутся в виде
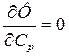 ,
, 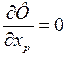 ,
, 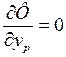 .
.
Откуда и определяются значения
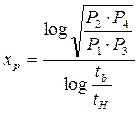 ,
, 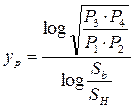 ,
, 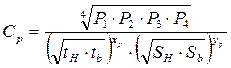 (8)
(8)
Методика проведения опытов
Опыты проводятся на токарном станке с ЧПУ. Обрабатываемый материал – Ст. 45, резец – Т15К6 (φ = 45°, γ = 10º). В современных станках с ЧПУ отсутствуют зубчатые колеса, что обусловливает бесшумную и практически безвибрационную работу станка. Привод главного движения состоит из регулируемого электродвигателя постоянного тока (мощностью до 30 кВт) от которого вращение передается через ременную зубчатую передачу непосредственно на шпиндель. Диапазон регулирования частот вращения шпинделя от 0 до 10000 об/мин. Рабочая зона станков полностью герметизирована, что позволяет применять интенсивное охлаждение и благоприятно сказывается на отводе стружки из рабочей зоны. Станки обеспечивают работу с повышенными скоростями резания (200…400 м/мин) при относительно малой глубине и подаче.
На станках предусмотрен контроль нагрузки (мощности) по координатным осям. Наибольшая нагрузка действует на шпиндель станка (ось z). Во время работы мощность на шпиндель станка высчитывается на панели управления. Часто «состояние» станка по мощности изображается по принципу «светофора»: зеленый, желтый и красный цвет. Зеленый цвет сигнализирует о нормальном состоянии станка, красный цвет – недопустим и требует изменения режимов обработки. Обычно о нагрузке на шпинделе судят по его деформации. Деформацию измеряют, как правило, с помощью тензометрических датчиков сопротивления. Тензодатчик преобразует деформацию шпинделя в электрический сигнал. Работа тензодатчика сопротивления основана на свойстве металлической проволоки диаметром 20-30 мкм при деформации (растяжение, сжатие) измерять свое электрическое сопротивления. Датчики включаются в мостиковую схему, сигнал, с которой поступает на панель управления. Нагрузка (мощность) измеряется в процентах, которые можно пересчитать в киловаттах, зная мощность привода главного движения (потери в приводе можно в первом приближении не учитывать).
Порядок выполнения работы
1. Составить план эксперимента
2. Провести измерения мощности резания в четырех независимых опытах при двух параллельных опытах для каждого независимого опыта и выполнить расчеты сил резания (4, 5) для этих опытов. Результаты записать в табл. 1.
Таблица 1
| № опыта | t, мм | S, мм/об | N, % | Pz, Н | Р z ср, Н | Примечание | ||
| 1 | 2 | 1 | 2 | |||||
| 1 | tH | SH | N11 | N12 | P11 | P12 | Р1 | |
| 2 | t В | SH | N21 | N22 | P21 | P22 | Р2 | |
| 3 | tH | S В | N31 | N32 | P31 | P32 | Р3 | |
| 4 | t В | S В | N41 | N42 | P41 | P42 | Р4 | |
3. Рассчитать коэффициенты математической модели Ср, x р , y р по формулам 6, 7 и 8.
4. Сравнить расчетные значения показателей степени x р и y р с нормативными.
5. Сделать выводы.
Дата: 2019-02-02, просмотров: 358.