Uф = z2 / z1 = 93 / 19 = 4,89. (29)
Отклонение фактического передаточного числа составляет
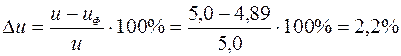 .
.
Для передач общемашиностроительного применения допускается отклонение фактического передаточного числа от номинального значения в пределах 4%.
Проверка прочности зубьев колес по контактным напряжениям проводится по следующему условию прочности
 , (30)
, (30)
где К HV 2 – коэффициент динамичности нагрузки зубьев колеса при контактных напряжениях. Он зависит от окружной скорости вращения колес V1 = V2, рассчитываемой по зависимости
 . (31)
. (31)
Окружная скорость вращения колес определяет их степень точности по ГОСТ 1643–81. Так при окружной скорости V2 до 2 м/с назначается 9-я степень точности, до V2 = 6 м/с – 8-я степень точности, до V2 = 10 м/с – 7-я степень точности.
Значения коэффициента КHV2 приведены в таблице 6.
По данным рассматриваемого примера V2 = 2,81 м/с. Этой скорости соответствует 8-я степень точности. Определим значение коэффициента КHV2 по таблице 6 с помощью линейной интерполяции. Видим, что коэффициент КHV2 = 1,112.
Таблица 6 – Значения КHV2 – коэффициента динамичности нагрузки при контактных напряжениях
| Степень точности | Окружная скорость V, м/с | |||||
| 1 | 2 | 4 | 6 | 8 | 10 | |
| 7 | – | – | – | 1,21 | 1,29 | 1,36 |
| 8 | – | 1,08 | 1,16 | 1,24 | – | – |
| 9 | 1,05 | 1,1 | – | – | – | – |
Действительное контактное напряжение по условию (30) равно
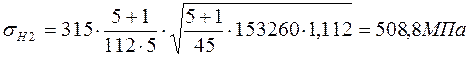 .
.
Допускаемая недогрузка передачи (sН2 < [ sН2]) возможна до 15%, а допускаемая перегрузка ( sН2 > [ sН2]) – до 5%. Если эти условия не выполняются, то необходимо изменить ширину колеса b2 или межосевое расстояние 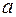 , и повторить расчет передачи.
, и повторить расчет передачи.
Фактическая недогрузка для рассматриваемого примера составит
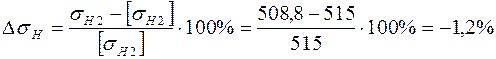 , (32)
, (32)
что меньше 15 %, а значит допустимо.
Расчетное максимальное напряжение при кратковременных перегрузках не должно превышать допускаемого значения
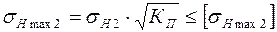 . (33)
. (33)
Для рассматриваемого примера расчета передачи
 .
.
Определим другие геометрические размеры колес, показанные на рисунке 2. Делительные диаметры равны
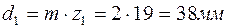 ,
,
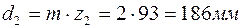 . (34)
. (34)
Диаметры вершин зубьев равны
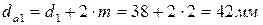 ,
,
 . (35)
. (35)
Диаметры впадин зубьев равны
 ,
,
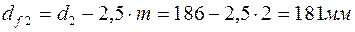 . (36)
. (36)
Проверим межосевое расстояние зубчатых колес
 . (37)
. (37)
В прямозубой цилиндрической передаче при работе появляются силы в зацеплении зубьев, показанные на рисунке 3.
Окружные силы определяют по зависимости
 (38)
(38)
Радиальные силы определяют по зависимости
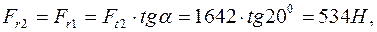 (39)
(39)
где a = 200 – угол зацепления.
Нормальная сила является равнодействующей окружной и радиальной сил в зацеплении и определяется по формуле
 (40)
(40)
Конструктивные размеры зубчатого колеса показаны на рисунке 4 и приведены в таблице 7. В качестве исходного размера используется диаметр посадочной поверхности вала dК под колесо, который будет получен в пункте 10 учебного пособия.
Таблица 7 – Размеры зубчатого колеса, мм
| Параметр (рисунок 4) | Формула | Расчет |
| Диаметр ступицы | dcт = 1,6 × dК | dcт = 1,6 × 45 = 72 |
| Длина ступицы | Lст = b2 … 1,5 × dК | Lст = 45 … 1,5 × 45 = = 45 … 67,5. Примем Lст = 55 мм |
| Толщина обода | dо = (2,5…4,0) × m | dо= (2,5…4,0) × 2 = 5…8 |
| Диаметр обода | Dо = dа2 – 2 ×dо– 4,5 × m | Dо=190–2 × 6– 4,5 × 2=169 |
| Толщина диска | c = (0,2…0,3) × b2 | с =(0,2…0,3) × 45 = 9…13 |
| Диаметр центров Отверстий в диске | Dотв = 0,5 × (Dо+ dcт) | Dотв= 0,5 × (169+72) = 120 |
| Диаметр отверстий | dотв = (Dо – dcт) / 4 | dотв = (169 – 72) / 4 = 24 |
| Фаски | n = 0,5 × m | n = 0,5 × 2 = 1 |
Расчет цепной передачи
Второй механической передачей в схеме рассматриваемого привода (рисунок А.1,б) является цепная передача, представленная на рисунке 5.
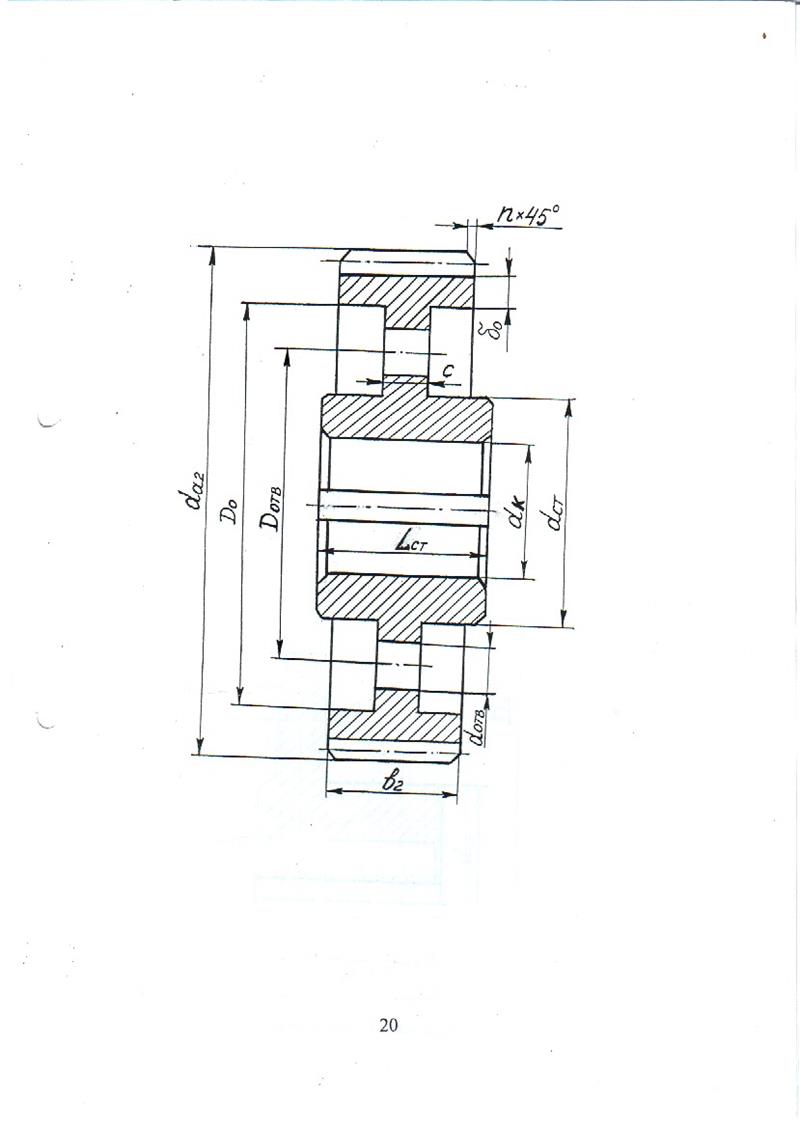
Рисунок 4 – Цилиндрическое зубчатое колесо
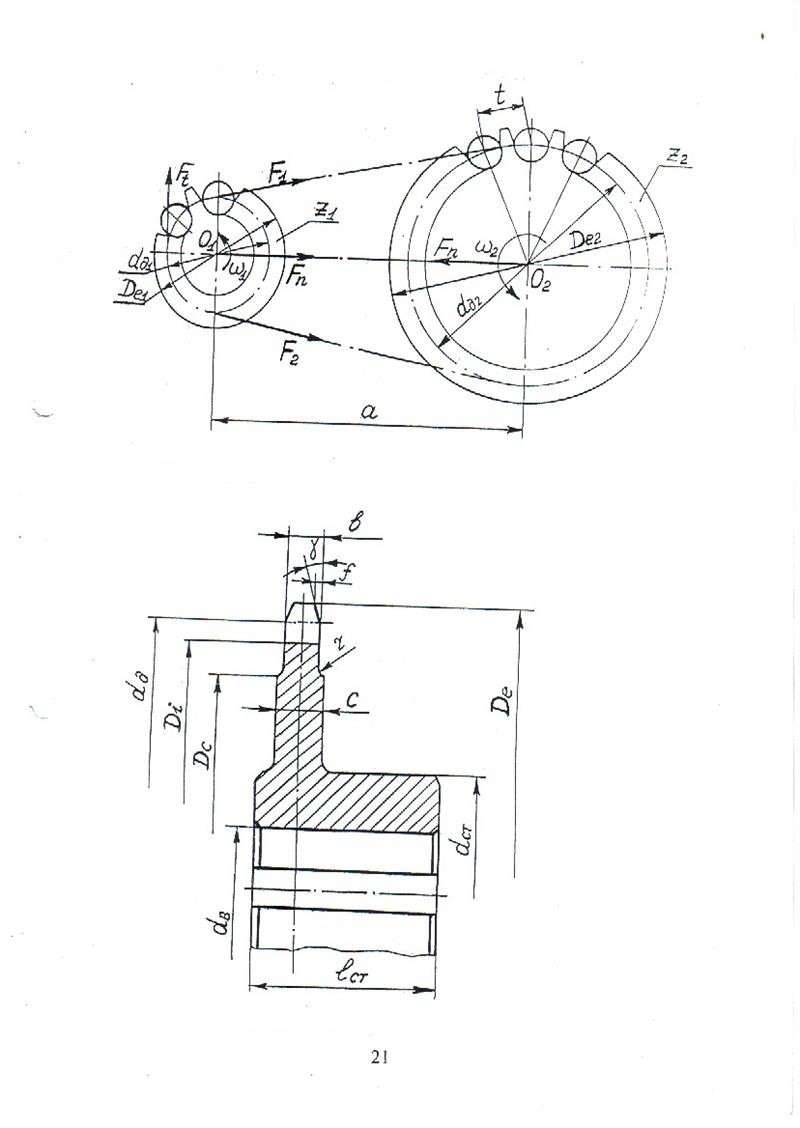
Рисунок 5 – Геометрические и силовые параметры цепной
передачи
Рисунок 6 – Конструкция ведущей звёздочки
Исходными данными для расчета цепной передачи являются следующие параметры (из пункта 6 учебного пособия):
– вращающий момент на валу ведущей звездочки (он равен моменту на третьем валу привода) Т1 = 153260 Н × мм;
– частота вращения ведущей звездочки (или частота вращения третьего вала привода) n1 = 289 мин–1;
– передаточное число цепной передачи u = uЦП= 3,212.
Методику расчета цепной передачи с приводной однорядной роликовой цепью проследим на рассматриваемом примере.
Важнейшим параметром цепной передачи является предварительное значение шага цепи t/, которое рассчитывается по допускаемому давлению в шарнире цепи по зависимости [3, с.92]:
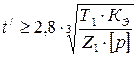 , (41)
, (41)
где КЭ – коэффициент эксплуатации, который представляет собой произве- дение пяти поправочных коэффициентов, учитывающих различные условия работы реальной передачи (таблица 8) [3,4]:
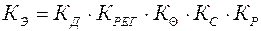 . (42)
. (42)
Выбрав в таблице 8 коэффициенты для условий работы рассчитываемой передачи, рассчитаем коэффициент КЭ :
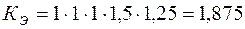 .
.
Определим Z/1 – предварительное число зубьев ведущей звездочки
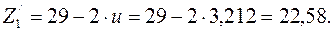 (43) Полученное предварительное значение Z/1 округляют до целого нечетного числа, что в сочетании с нечетным числом зубьев ведомой звездочки Z2 и четным числом звеньев цепи Lt обеспечит более равномерное изнашивание зубьев. Принимаем Z1 = 23. Тогда Z2 = Z1 × u = 23 × 3,212 = 73,88. Принимаем Z2 =73 (нечетное число).
(43) Полученное предварительное значение Z/1 округляют до целого нечетного числа, что в сочетании с нечетным числом зубьев ведомой звездочки Z2 и четным числом звеньев цепи Lt обеспечит более равномерное изнашивание зубьев. Принимаем Z1 = 23. Тогда Z2 = Z1 × u = 23 × 3,212 = 73,88. Принимаем Z2 =73 (нечетное число).
Уточним передаточное число цепной передачи
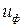 = Z2 / Z1 = 73 / 23 = 3,174. (44)
= Z2 / Z1 = 73 / 23 = 3,174. (44)
Допускается отклонение от расчетного значения 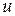 не более ±4 %
не более ±4 %
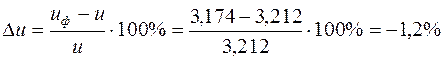 . (45)
. (45)
Последним параметром в формуле (41) является [p] – допускаемое давление в шарнире цепи, Н/мм2. Оно определяется в зависимости от скорости цепи 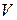 по ряду [4]:
по ряду [4]:
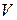 , м/с , м/с
| 0,1 | 0,4 | 1 | 2 | 4 | 6 | 8 | 10 |
| [p], Н/мм2 | 32 | 28 | 25 | 21 | 17 | 14 | 12 | 10 |
Если не известны дополнительные данные, то задаются предварительным значением 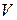 = 2 … 3 м/с. Примем
= 2 … 3 м/с. Примем 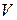 = 2,5 м/с, тогда интерполированием получаем [p] = 20 Н/мм2.
= 2,5 м/с, тогда интерполированием получаем [p] = 20 Н/мм2.
Таблица 8 – Значения поправочных коэффициентов К
Условия работы передачи
Коэффициент
Рассчитаем по зависимости (41) шаг цепи
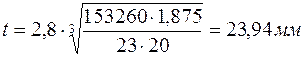 .
.
Полученное значение шага округляется до ближайшего большего стандартного значения по таблице Б.1 – t = 25,4мм.
Определим фактическую скорость цепи
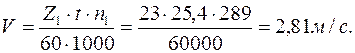 (46)
(46)
Этой скорости цепи в соответствии с вышеприведенным рядом соответствует допускаемое давление [p] = 19,38 Н/мм2.
Дата: 2019-02-02, просмотров: 740.