Определим работу расширения в политропном процессе.
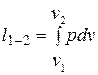. (2.38)
В соответствии с основным уравнением политропы
,
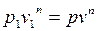где p , v – текущие значения давления и объема в ходе процесса.
Отсюда
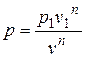. (2.39)
Совместное решение (2.38) и (2.39) дает
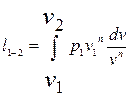
или
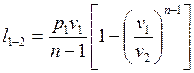, (2.40)
.
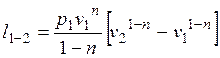Для работы идеального газа справедливы следующие выражения
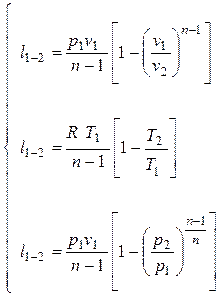(2.40а)
Частные случаи политропного процесса
При рассмотрении политропного процесса предполагалось, что все параметры состояния меняются в ходе процесса, что имеет место обмен энергией между системой и окружающей средой. Вместе с тем, существует группа процессов, при протекании которых накладывается запрет на изменение того или иного параметра состояния, на тот или иной вид энергетического обмена с окружающей средой. Различают четыре вида таких процессов. Это изохорный (v = const), изобарный (р = const), изотермический (T = const) и адиабатный или изоэнтропный (s = const). Рассмотрим эти процессы.
Изохорный процесс
В данном случае запрещается изменение объема (v = const).
Теплоемкость системы
.
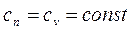Определим значение n при v = const. Из (2.19) следует
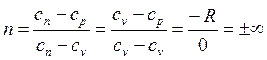
Извлечем корень n-ой степени из (2.22)
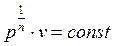
и подставим в него найденное значение показателя политропы. Тогда получим
.
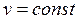Таким образом, из общего уравнения политропы получено уравнение изохорного процесса. Последнее позволяет рассматривать изохорный процесс как частный случай политропного процесса при n =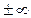 
.
Определим соотношение между параметрами в изохорном процессе.
Для изохорного процесса имеет смысл искать соотношение лишь между Р и Т, т.к. при v = const отыскание взаимосвязи между Р и v или Т и v лишено смысла.
В общем случае протекания политропного процесса соотношение Р и Т устанавливалось (2.26)
.
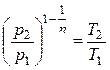Если ввести в него n =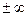 
, то
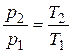. (2.41)
Выражение (2.41) известно из физики как закон Шарля.
Изменение внутренней энергии
.
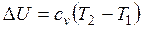Изменение энтальпии
.
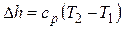Изменение энтропии определяется из выражения (2.34)
.
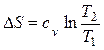Работа расширения
.
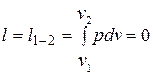Из первого закона термодинамики следует
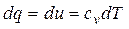
или
.
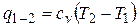Изобарный процесс
В данном случае накладывается запрет на изменение давления (p = const).
Теплоемкость системы
.
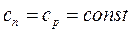Определим значение n при р = const. Из (2.19) следует
.
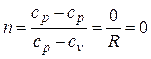Если в основное уравнение политропы подставить найденное значение n, то
, 
.
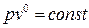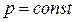При рассмотрении изобарного процесса имеет смысл искать соответствие между основными параметрами состояния лишь в виде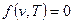 
. Уравнение (2.25) при 
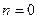дает
- закон Гей-Люссака.
То есть в изобарном процессе изменение объема прямо пропорционально изменению абсолютной температуры.
Изменение внутренней энергии идеального газа не зависит от пути процесса, т.е. U в случае p = const
.
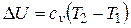Изменение энтальпии
.
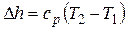Изменение энтропии определяется из выражения (2.35)
.
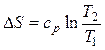Работа, производимая газом в ходе изобарного расширения или затрачиваемая на его изобарное сжатие, легко может быть определена по формуле политропного процесса при условии, что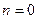 
. Это условие сводит все формулы работы политропного процесса к двум:
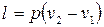(2.42)
и
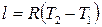. (2.43)
Следует отметить, что уравнение (2.42) может быть получено для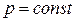 
из самого общего выражения работы (2.38) без каких-либо оговорок относительно природы газа. Поэтому данная формула справедлива как для реальных, так и для идеальных газов.
Рассмотрение (2.43) представляет дополнительный интерес в связи с тем, что оно позволяет раскрыть физический смысл газовой постоянной. Действительно, если решить (2.43) относительно газовой постоянной
,
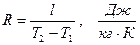то последняя представляется как работа расширения в изобарном процессе 1 кг идеального газа при изменении его температуры на 1 градус.
Тепло, подводимое (отводимое) в ходе изобарного процесса, можно найти с помощью уравнения первого начала термодинамики
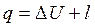
или с помощью теплоемкости:
.
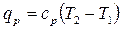Изотермический процесс
Теплоемкость
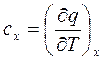(2.44)
в случае изотермического процесса (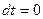 
), как видно из (2.44) равна бесконечности. Уравнение (2.19) при подстановке в него 
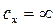дает неопределенность вида 
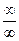, раскрытие которой в данном случае может быть осуществлено путем вычитания из обеих его частей по единице:
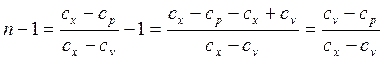
при подстановке
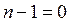
или
.
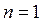Если в основное уравнение политропы (2.22) подставить найденное значение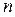 
, то получим
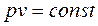(2.45)
представляющее собой математическую запись закона Бойля-Мариотта.
Таким образом, изотермический процесс изменения состояния идеального газа – частный случай политропного процесса, когда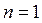 
.
Как следует из уравнения (2.45), в системе координат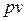 
изотермический процесс изменения состояния идеального газа представляет собой равнобокую гиперболу, асимптотами которой являются оси координат.
При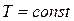 
переменными оказываются лишь два основных параметра состояния, взаимосвязь между которыми определяется уравнением (2.45). В соответствии с последним
.
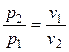Внутренняя энергия идеального газа включает в себя лишь внутреннюю кинетическую энергию, которая однозначно связана с температурой. Поэтому при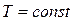 
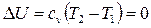. (2.46)
Изменение энтальпии
.
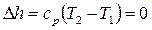Изменение энтропии определяется из уравнений (2.34) и (2.35), которые при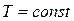 
принимают следующий вид:
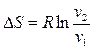
и
.
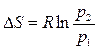Формулы работы, производимой идеальным газом при изотермическом расширении, могут быть получены из уравнений работы, полученных для общего случая политропного процесса. Однако, простая подстановка в уравнение (2.40)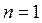 
с учетом 
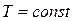и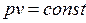 
приводит к неопределенности типа 
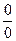. Используем для этой цели уравнение (2.40), применив к нему правило Лопиталя. Обозначим в уравнении (2.40)
.
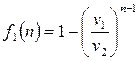
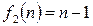Тогда (2.40) примет вид:
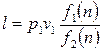(2.47)
В соответствии с правилом Лопиталя при неопределенности типа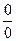 
или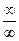 
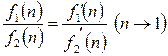(2.48)
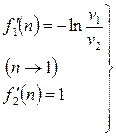. (2.49)
Решая совместно (2.47), (2.48) и (2.49), получим
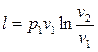. (2.50)
Учитывая (2.46), уравнение первого начала термодинамики для изотермического процесса изменения состояния сведется к виду
.
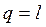Таким образом, в изотермическом процессе изменения состояния идеального газа все подводимое к телу тепло идет на совершение работы расширения.
Адиабатный процесс
Адиабатным называется процесс, в ходе которого система не может обмениваться теплом с окружающей средой. Необходимым и достаточным условием адиабатного процесса является
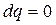. (2.51)
Для адиабатного процесса в соответствии с (2.51) теплоемкость
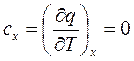. (2.52)
Если рассмотреть (2.19), учитывая (2.52), то в данном случае
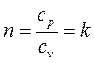, (2.53)
где k – показатель адиабаты.
Основное уравнение адиабаты получается из (2.22) с учетом (2.53)
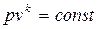. (2.54)
Иначе говоря, адиабатный процесс – это частный случай политропного процесса, когда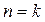 
.
В системе координат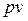 
адиабатный процесс изображается кривой, близкой к гиперболе. Эта кривая называется адиабатой.
В обратимом адиабатном процессе не происходит изменения энтропии
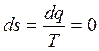или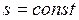 
. (2.55)
В системе координат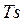 
обратимый адиабатный процесс изображается линией 
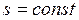. Поэтому данный процесс иначе называют изоэнтропийным.
Формулы соотношения между основными параметрами состояния получаются из соответствующих выражений политропного процесса при замене в них показателя политропы на показатель адиабаты:
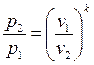(2.56)
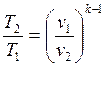(2.57)
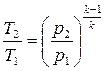. (2.58)
То же самое получается с формулами для определения работы:
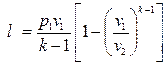
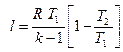
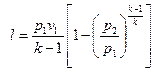
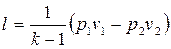
Как и в любом другом процессе изменения состояния идеального газа изменение внутренней энергии определяется уравнением
.
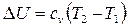В связи с тем, что в адиабатном процессе запрещен теплообмен с окружающей средой, уравнение первого начала термодинамики принимает вид:
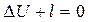
или
.
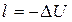Иначе говоря, в адиабатном процессе работа расширения совершается за счет внутренней энергии системы. Наоборот, при сжатии вся затраченная на сжатие работа расходуется на увеличение внутренней энергии. По этой причине температура системы при адиабатном расширении падает, а при сжатии - возрастает.
Таблица 2.1
Сводная таблица частных случаев политропного процесса
| Процесс | n | Соотношения параметров | DU | Dh | DS | q | l |
| Изохорный v = const |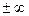 
| 
| 
| 
| 
| 
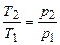
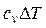
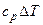
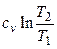
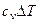
| 0 |
| Изобарный P = const |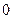 
| 
| 
| 
| 
| 
| 
|
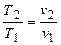
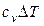
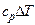
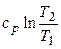
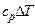
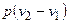
| Изотермический T = const | 1 |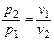 
| 0 | 0 |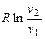 
| 
| 
|
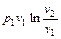
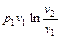
| Адиабатный dq = 0 | k |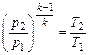 
| 
| 
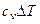
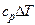
| 0 | 0 |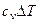
|
Дата: 2019-02-02, просмотров: 284.
