Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

ЛЕКЦИЯ 1

ОРГАНИЧЕСКИЕ ТОПЛИВА

 

Топлива – это природные вещества которые экономически целесообразно использовать для получения теплоты в больших количествах. Различают химические и ядерные топлива. Мы будем рассматривать только химические органические топлива, применяемые в промышленности и энергетике.

Топливо представляет собой совокупность горючего и окислителя.

К горючим относят водород (Н₂); щелочные металлы: натрий (Na), магний (Mg), алюминий (Al), калий (K); углерод (С) и углеводородные соединения.

К окислителям относят кислород (О₂), соединения с кислородом и элементы гомогенного ряда: фтор (F), хлор (Cl).

        

В таблице 1.1 приведена классификация углеводородных горючих по происхождению и агрегатному состоянию.

 

Таблица 1.1

Классификация углеводородных горючих

 

Происхождение Агрегатное состояние	Природные	Искусственные
Твердое	древесина, торф, бурый уголь, каменный уголь, полуантрацит, антрацит, горючие сланцы	кокс, древесный уголь, брикеты
Жидкое	нефть, газовый конденсат        (белая нефть)	продукты переработки нефти: бензин, лигроин, керосин, соляровое масло (газойль), мазут; спирты
Газообразное	природный газ, попутный газ	генераторные газы, газы сухой перегонки, доменный и коксовый газы, светильный газ, биогаз

 

Состав топлив

 

    Свойства топлив, целесообразность их использования в значительной мере определяются их химическим составом, который для жидких и твердых топлив задается обычно в процентах по массе. Состав газового топлива задается объемным содержанием в % входящих в него газов.

    Элементы, входящие в состав топлива, обозначаются соответствующими символами: С – углерод; Н – водород; О – кислород; N – азот; S – сера. Зола и влага, входящие в состав топлива, обозначаются соответственно А и W.

    Влажность и зольность топлив даже в пределах одного сорта подвержены значительным колебаниям, поэтому для уточнения характеристик вводятся понятия о горючей, сухой и рабочей массах топлива. Обратите внимание на различия уравнений материального баланса для этих случаев.

    Материальный баланс горючей  массы углеводородного топлива

C_г + H_г + O_г+ N_г + S_г = 100 %.

Материальный баланс сухой массы:

С_c + H_c + O_c + N_c + S_c + A_c = 100 %.

 

Материальный баланс рабочей массы

С_p + H_p + O_p + N_p + S_p + A_p + W_p = 100 %.

Совокупность золы и влаги, входящих в состав топлива, называют внешним балластом горючего. Совокупность кислорода и азота, входящих в состав топлива, называют  внутренним балластом горючего.

 

Характеристики топлив

    К основным характеристикам, определяющих ценность топлив, относят следующие.

1. Вязкость.

2. Температура воспламенения.

3. Температура вспышки.

4. Токсичность.

5. Температура замерзания.

6. Температура перегонки.

7. Запыленность (для газообразных горючих).

8. Теплота сгорания Q, Дж – это количество теплоты, выделяющейся при полном сгорании горючего.

 

Для инженерных расчетов процессов горения пользуются понятием - удельная теплота сгорания q , Дж/кг - это количество теплоты, выделяющейся при полном сгорании 1кг твердого (жидкого) или одного нормального кубического метра (1 нм³) газообразного горючего.

1 нм³ - это кубический метр при нормальных условиях (t = 0 ­­⁰C, Р = 760 мм. рт. ст.).

 

Принято различать высшую и низшую теплоту сгорания.

q_в = q_н +0,025 (9H_р + W_p), МДж / кг,

 

где q_в - высшая теплота сгорания – это количество теплоты, выделяющейся при сгорании топлива с учетом теплоты конденсации водяных паров, образующихся при сгорании водорода Н_р и испарении влаги W_p;

  q_н - низшая теплота сгорания – теплота сгорания топлива, при условии, что влага, образующаяся при сгорании водорода топлива 9Н_р и влага топлива W_p находятся в парообразном состоянии;

0,025 МДж/кг - теплота парообразования воды;

9Н_р – количество влаги, выделяющейся при полном сгорании рабочей массы водорода топлива;

W_р – количество влаги, которое содержится в горючем.

 

Самым калорийным горючим является - водород (Н₂).

 

q_н = 140 МДж/кг - для водорода;

q_н = 20-30 МДж/кг - для каменного угля;

q_н = 38 МДж/кг - для мазута.

 

Условное топливо - это такое эффективное, несуществующее в природе топливо, теплота сгорания которого

q_усл = 29,33 МДж/кг (7000 ккал/кг).

 

Условный эквивалент - это отношение низшей теплоты сгорания горючего к теплоте сгорания условного топлива:

В_усл = q_н/q_усл.

 

В России на гражданина приходится примерно около 2 тонн условного топлива в год. В развитых странах (США, Великобритания, Германия) на гражданина приходится примерно около 10 тонн условного топлива в год.

 

Разновидности горения

 

Горением называется химическая реакция взаимодействия горючего с окислителем, сопровождающаяся интенсивным выделением теплоты и резким повышением температуры.

Горение возможно только в газообразной фазе.

Если горючее и окислитель находятся в одной газообразной фазе, то горение называют гомогенным.

Если один из компонентов топлива находится в отличном от газообразного состояния, то горение называют гетерогенным.

При гетерогенном горении происходит изменение агрегатного состояния вещества.

 

Фазы горения

    Время, за которое происходит полное сгорание топлива можно условно разделить на два этапа:

t_г = t_ф + t_к,

где t_г -  продолжительность горения;

      t_ф  -  физическая фаза (время смесеобразования);

      t_к - кинетическая фаза (время химической реакции окисления).

 

В зависимости от продолжительности той или иной фазы, различают два предельных случая:

 1) t_ф >> t_к - диффузионное горение (факельное сжигание топлива, горение спички, горелки);

 2) t_к  >> t_ф - кинетическое горение (взрыв).

 

ЛЕКЦИЯ 2

 

Скорость горения

    Под скоростью горения понимают скорость, с которой перемещается фронт пламени.

    Нормальная скорость распространения фронта пламени (Uн), обозначается вектором, направленным перпендикулярно ко фронту пламени.

    В зависимости от величины скорости перемещения фронта пламени, различают нормальное и детонационное горение.

Uн = 0,4 - 50 м/с  -  нормальное горение,

где Uн = 0,4 - 13 м/с -  ламинарное горение (пламя);

Uн = 13 - 50 м/с  -  турбулентное горение.

Uн = 1500 - 3500 м/с  -  детонационное горение.

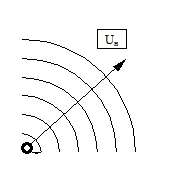
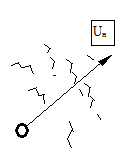
а)                                  б)

Рис.1.1

На рисунке 1.1 а приведена схема ламинарного горения от точечного источника. При этом режиме горения фронт пламени гладкий (горение спички, свечи). На рисунке. 1.1 б приведена схема турбулентного горения от точечного источника. При этом режиме горения фронт пламени размытый (горение горелки при большой подаче горючего).

 

РАСЧЕТ ПРОЦЕССОВ ГОРЕНИЯ

 

Основные цели расчета процесса горения сводятся к определению следующих величин.

1. Определение потребного количества окислителя для полного сжигания 1кг горючего.

2. Определение количества и состава продуктов сгорания.

3. Определение температуры конца сгорания продуктов сгорания.

4. Определение теплосодержания (энтальпии) продуктов сгорания.

 

 

Коэффициент избытка воздуха

 

В действительности подаваемое количество воздуха отличается от теоретически необходимого. Из-за несовершенства процессов смесеобразования в энергетических установках, где стремятся максимально полно использовать энергию топлива, приходится подавать воздух в количествах, превышающих теоретически необходимое. В печах безокислительного нагрева металла, чтобы поддержать восстановительную атмосферу печи, воздуха подают меньше, то есть сознательно идут на недожег топлива.

Отношение действительно поданного воздуха ( 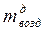) к его теоретически необходимому количеству ( ) представляет собой коэффициент избытка воздуха ( ):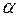

.

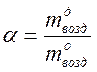При сжигании древесины 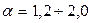; углей - 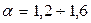; при сжигании газа и мазута 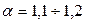; в дизелях минимальные значения  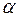близки к 1,3; карбюраторные двигатели работают в диапазоне значений  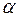от 0,8 до 1,2 (в зависимости от режима работы и конструкции двигателя).

 

Различают три вида топливных смесей, в зависимости от значения .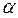

При 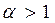смеси называются бедными (окислителя в зону реакции подается больше, чем требуется для полного сгорания горючего). В продуктах сгорания таких смесей содержатся следующие элементы: Н₂О, СО₂, SO₂, N₂, О₂.

При 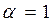смеси называются стехиометрическими (окислителя в зону реакции подается столько, сколько требуется для полного сгорания горючего). В продуктах сгорания таких смесей содержатся следующие элементы: Н₂О, СО₂, SO₂, N₂.

При 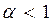смеси называются богатыми (окислителя в зону реакции подается меньше, чем требуется для полного сгорания горючего). В продуктах сгорания таких смесей содержатся следующие элементы: Н₂О, СО₂, СО, С, N₂.

 

 

Лекция 3

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ ТЕРМОДИНАМИКИ

 

В термодинамике объектом изучения является термодинамическая система, под которой понимают совокупность тел, которые могут энергетически взаимодействовать между собой и с другими телами и обмениваться с ними веществом.

Внешние, по отношению к выделенной термодинамической системе тела, носят название окружающей среды.

Различают закрытые и открытые системы. В первом случае отсутствует обмен веществом между системой и средой. Во втором случае такой обмен имеет место.

Энергетическое взаимодействие между системой и окружающей средой заключается, в общем случае, в обмене работой и теплотой.

Первый способ передачи энергии – это работа, хорошо известен из механики. Произведенная (или полученная) работа определяется произведением силы на перемещение в направлении ее действия. Таким образом, в этом случае при передаче энергии температура тел роли не играет.

В термодинамике работа обозначается L, если она отнесена ко всей системе, и через l, если к 1кг ее массы. Принято считать работу положительной в том случае, когда система производит работу над окружающей средой. Если среда производит работу над системой, то в этом случае работа считается отрицательной.

L , Дж; l, Дж/кг.

 

Второй способ передачи энергии – это теплота, характерен тем, что энергия, передаваемая одним телом другому при их взаимодействии зависит только от температуры этих тел.

В термодинамике принято обозначать тепло, полученное (отданное) всей системой - Q, а отнесенное к единице массы системы - q. При этом принято считать теплоту, полученную системой, положительной.

 

Q , Дж; q, Дж/кг.

 

Системы, не имеющие никаких взаимодействий с окружающей средой, называются изолированными.

Если между системой и окружающей средой из всех взаимодействий отсутствует лишь теплообмен, то такая система называется адиабатной.

В термодинамике термодинамическими системами являются тела, посредством которых осуществляется преобразование теплоты в работу и обратно. Их называют рабочими телами.

 

 

ПАРАМЕТРЫ СОСТОЯНИЯ СИСТЕМЫ

 

Каждое конкретное состояние термодинамической системы может быть охарактеризовано рядом величин, которые называются термодинамическими параметрами.

Если значение параметров системы во всех точках ее объема одинаково, такая система называется равновесной. Математический аппарат классической термодинамики, строго говоря, применим лишь к таким состояниям.

Одна часть параметров может быть непосредственно измерена простыми техническими средствами. Эти параметры называют основными. Другая часть находится расчетным путем с помощью основных параметров состояния.

В термодинамике в качестве основных параметров состояния используются: абсолютное давление, абсолютная температура и удельный объем.

Абсолютное давление – это сила, действующая по нормали к поверхности и отнесенная к единице площади этой поверхности.

В качестве единиц измерения давления используются:

1. Техническая атмосфера 1ат = 1 .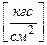

2. Физическая атмосфера. Одна физическая атмосфера эквивалентна давлению, которое оказывает столб ртути высотой 760 мм при t = 0 ⁰С.

3. Паскаль 1Па = ;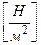

4. Бар 1бар = ;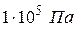

5. Миллиметры ртутного столба мм.рт.ст.

6. Миллиметры водного столба мм.вод.ст.

 

В системе СИ единицей измерения давления является Паскаль (Па).

Следует напомнить, что кроме барометров, все приборы для измерения давления фиксируют разницу между измеряемым абсолютным давлением Р и давлением окружающей среды Р_о.

Р = Р_м + Р_о , где Р_м – показания манометра.

 

Если абсолютное давление ниже давления окружающей среды (вакуум), то

 

Р = Р_о - Р_вак , где Р_вак – показания вакуумметра.

 

Абсолютная температура Т является важнейшим параметром состояния. Она характеризует тепловое состояние тела.

 

Т, К; t, ⁰С;    Т = t + 273.

Удельный объем – это объем, занимаемый единицей массы вещества, составляющего систему.

Если принять, что масса системы m кг, ее объем V м³, то удельный объем:

 

v = 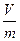  м­³/кг.

Вместо удельного объема можно оперировать понятием плотность. Плотностью вещества ρ называют массу вещества, заключенную в единице объема:

 

ρ = m / v кг/м­³.

 

Для равновесной, однородной термодинамической системы существует определенная аналитическая зависимость между основными параметрами состояния:

f ( P , v , T ) = 0,                                                 (2.1)

которая называется уравнением состояния.

Из уравнения (2.1) следует, что независимыми параметрами могут быть лишь два каких-либо параметра, которые и определяют значение третьего.

В наиболее простом случае:

 

Р V_μ = R_μ T ,                                                         (2.2)

 

где V_μ  – объем моля газа (при н.у. V_μ = 22,4 м³);

R_μ = 8314 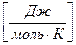 – универсальная газовая постоянная.

Газ, для которого справедливо уравнение (2.2) называется идеальным. Модель идеального газа представляет собой газ, молекулы которого рассматриваются как материальные точки, взаимодействие которых между собой ограничено упругими соударениями.

Для 1кг идеального газа уравнение состояния имеет вид:

 

Р v = R T ,                                                    (2.3)

где 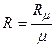  – газовая постоянная .

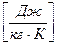Газовая постоянная (в отличие от универсальной газовой постоянной) является характеристикой для каждого газа постоянной, численно равной отношению универсальной газовой постоянной (R_μ) к массе моля данного газа ( μ). Величину R иногда называют характеристической газовой постоянной.

Если в результате взаимодействия с окружающей средой меняется хотя бы один из параметров состояния системы, то говорят об изменении ее состояния.

Изменение состояния системы, характеризующееся изменением ее термодинамических параметров, называют термодинамическим процессом.

 

Все процессы, происходящие в термодинамической системе, можно разделить на равновесные и неравновесные.

Равновесный процесс представляет собой непрерывный ряд равновесных состояний.

Большую роль в термодинамике играют понятия – обратимые и необратимые процессы.

Обратимым называется процесс, после которого система и окружающая среда могут возвращаться в начальное состояние. Обратимыми могут быть лишь равновесные процессы.

В реальных условиях обратимых процессов не существует. Все реальные процессы необратимые. Типичным примером необратимого процесса является процесс трения. Работа, затрачиваемая на преодоление трения, необратимо превращается в тепло.

Классический аппарат термодинамики применим лишь к равновесным обратимым процессам.

Все параметры термодинамической системы (в том числе и ранее рассмотренные P , v и T) отличаются той особенностью, что их изменение не зависит от вида процесса, а целиком определяется начальным и конечным состоянием системы, т.е. любой параметр – функция состояния.

Кроме перечисленных ранее основных параметров состояния (P , v и T), в термодинамике исключительно важную роль играют следующие параметры состояния: внутренняя энергия, энтальпия и энтропия.

Внутреннюю энергию системы в термодинамике рассматривают как сумму кинетической энергии составляющих ее частиц и потенциальной энергии, обусловленной их взаимным притяжением.

Внутренняя энергия всей системы обозначается U , [Дж], а отнесенная к единице массы u , .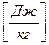

Как известно из физики, кинетическая энергия частиц однозначно связана с абсолютной температурой.

Потенциальная энергия системы при прочих равных условиях определяется расстоянием между частицами, которое в интегральной форме может характеризоваться удельным объемом.

Таким образом:

U = U ( T , v ).

В идеальном газе отсутствует взаимное притяжение между частицами, поэтому его внутренняя энергия не зависит от объема и включает в себя лишь кинетическую составляющую:

U = U ( T ).

Энтальпия – это функция состояния (параметр состояния), представляющая собой сумму внутренней энергии и произведения абсолютного давления на объем.

Энтальпия всей системы равна:

Н = U + PV.

 

Энтальпия, отнесенная к 1 кг массы системы:

h = u + Р v .

В термодинамике для обозначения энтальпии иногда используют букву I – для обозначения энтальпии всей системы и i – для обозначения удельной энтальпии, т.е. H 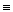I , a h 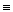i .

    Энтропия – это функция состояния системы (S), определяемая тем, что ее дифференциал при элементарном равновесном процессе (dS) равен отношению бесконечно малого количества теплоты (dQ), сообщенной системе, к абсолютной температуре системы.

Энтропия всей системы равна

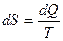.                                                   (2.4)

Энтропия, отнесенная к 1 кг массы системы

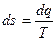.                                                  (2.5)

    Энтальпия и энтропия, являясь параметрами состояния системы, могут быть, как и внутренняя энергия, представлены в виде функции любых двух других параметров состояния. Например

h = h ( p , T );

s = s ( p , v ).

Рис. 2.1.                                                                     Рис. 2.2.

 

 

Лекция 4

 

Политропный процесс

Политропным называется процесс, в ходе которого неизменной остается только теплоемкость, все остальные параметры изменяются.

,

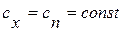где 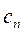- теплоемкость политропного процесса.

 

Изохорный процесс

 

В данном случае запрещается изменение объема (v = const).

Теплоемкость системы

.

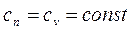Определим значение n при v = const. Из (2.19) следует

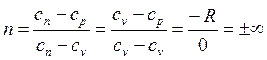
Извлечем корень n-ой степени из (2.22)

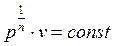
и подставим в него найденное значение показателя политропы. Тогда получим

.

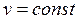Таким образом, из общего уравнения политропы получено уравнение изохорного процесса. Последнее позволяет рассматривать изохорный процесс как частный случай политропного процесса при n = .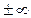

 

Определим соотношение между параметрами в изохорном процессе.

Для изохорного процесса имеет смысл искать соотношение лишь между Р и Т, т.к. при v = const отыскание взаимосвязи между Р и v или Т и v лишено смысла.

В общем случае протекания политропного процесса соотношение Р и Т устанавливалось (2.26)

.

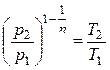Если ввести в него n = 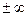, то

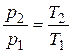.                                    (2.41)

    Выражение (2.41) известно из физики как закон Шарля.

Изменение внутренней энергии

.

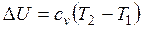Изменение энтальпии

.

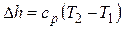Изменение энтропии определяется из выражения (2.34)

.

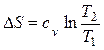Работа расширения

.

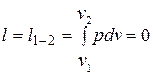Из первого закона термодинамики следует

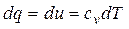
или

.

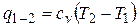Изобарный процесс

 

В данном случае накладывается запрет на изменение давления (p = const).

Теплоемкость системы

.

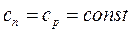Определим значение n при р = const. Из (2.19) следует

.

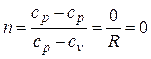    Если в основное уравнение политропы подставить найденное значение n, то

, .

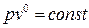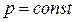    При рассмотрении изобарного процесса имеет смысл искать соответствие между основными параметрами состояния лишь в виде 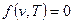. Уравнение (2.25) при  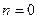дает

- закон Гей-Люссака.

    То есть в изобарном процессе изменение объема прямо пропорционально изменению абсолютной температуры.

    Изменение внутренней энергии идеального газа не зависит от пути процесса, т.е. U в случае p = const

.

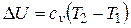Изменение энтальпии

.

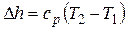Изменение энтропии определяется из выражения (2.35)

.

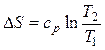Работа, производимая газом в ходе изобарного расширения или затрачиваемая на его изобарное сжатие, легко может быть определена по формуле политропного процесса при условии, что 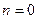. Это условие сводит все формулы работы политропного процесса к двум:

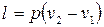                                         (2.42)

и

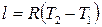.                                       (2.43)

 

    Следует отметить, что уравнение (2.42) может быть получено для 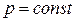 из самого общего выражения работы (2.38) без каких-либо оговорок относительно природы газа. Поэтому данная формула справедлива как для реальных, так и для идеальных газов.

    Рассмотрение (2.43) представляет дополнительный интерес в связи с тем, что оно позволяет раскрыть физический смысл газовой постоянной. Действительно, если решить (2.43) относительно газовой постоянной

,

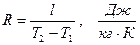то последняя представляется как работа расширения в изобарном процессе 1 кг идеального газа при изменении его температуры на 1 градус.

    Тепло, подводимое (отводимое) в ходе изобарного процесса, можно найти с помощью уравнения первого начала термодинамики

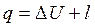
    или с помощью теплоемкости:

 

.

 

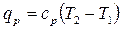Изотермический процесс

    Теплоемкость

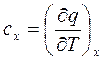                                        (2.44)

в случае изотермического процесса ( 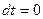), как видно из (2.44) равна бесконечности. Уравнение (2.19) при подстановке в него  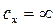дает неопределенность вида 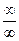, раскрытие которой в данном случае может быть осуществлено путем вычитания из обеих его частей по единице:

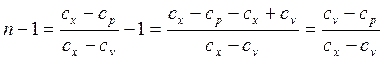
при подстановке

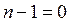
или

.

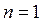    Если в основное уравнение политропы (2.22) подставить найденное значение 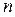, то получим

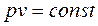                                         (2.45)

представляющее собой математическую запись закона Бойля-Мариотта.

    Таким образом, изотермический процесс изменения состояния идеального газа – частный случай политропного процесса, когда .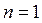

    Как следует из уравнения (2.45), в системе координат 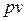 изотермический процесс изменения состояния идеального газа представляет собой равнобокую гиперболу, асимптотами которой являются оси координат.

    При 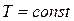 переменными оказываются лишь два основных параметра состояния, взаимосвязь между которыми определяется уравнением (2.45). В соответствии с последним

.

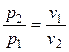    Внутренняя энергия идеального газа включает в себя лишь внутреннюю кинетическую энергию, которая однозначно связана с температурой. Поэтому при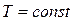

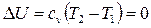.                                       (2.46)

Изменение энтальпии

.

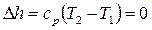Изменение энтропии определяется из уравнений (2.34) и (2.35), которые при 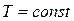 принимают следующий вид:

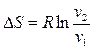
и

.

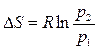    Формулы работы, производимой идеальным газом при изотермическом расширении, могут быть получены из уравнений работы, полученных для общего случая политропного процесса. Однако, простая подстановка в уравнение (2.40) 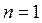 с учетом  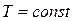и 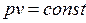 приводит к неопределенности типа 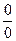. Используем для этой цели уравнение (2.40), применив к нему правило Лопиталя. Обозначим в уравнении (2.40)

.

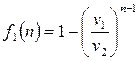
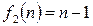Тогда (2.40) примет вид:

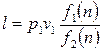                           (2.47)

В соответствии с правилом Лопиталя при неопределенности типа 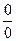 или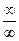

 

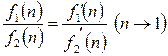                            (2.48)

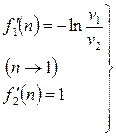.                                     (2.49)

 

Решая совместно (2.47), (2.48) и (2.49), получим

 

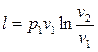.                                        (2.50)

 

    Учитывая (2.46), уравнение первого начала термодинамики для изотермического процесса изменения состояния сведется к виду

.

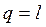    Таким образом, в изотермическом процессе изменения состояния идеального газа все подводимое к телу тепло идет на совершение работы расширения.

 

Адиабатный процесс

 

    Адиабатным называется процесс, в ходе которого система не может обмениваться теплом с окружающей средой. Необходимым и достаточным условием адиабатного процесса является

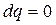.                                       (2.51)

    Для адиабатного процесса в соответствии с (2.51) теплоемкость

 

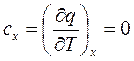.                                          (2.52)

    Если рассмотреть (2.19), учитывая (2.52), то в данном случае

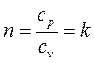,                                                  (2.53)

        где k – показатель адиабаты.

    Основное уравнение адиабаты получается из (2.22) с учетом (2.53)

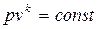.                                        (2.54)

    Иначе говоря, адиабатный процесс – это частный случай политропного процесса, когда .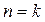

    В системе координат 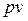 адиабатный процесс изображается кривой, близкой к гиперболе. Эта кривая называется адиабатой.

    В обратимом адиабатном процессе не происходит изменения энтропии

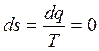 или 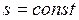.                          (2.55)

В системе координат 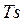обратимый адиабатный процесс изображается линией 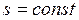. Поэтому данный процесс иначе называют изоэнтропийным.

    Формулы соотношения между основными параметрами состояния получаются из соответствующих выражений политропного процесса при замене в них показателя политропы на показатель адиабаты:

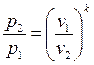                                         (2.56)

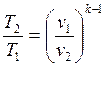                                  (2.57)

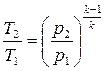.                                         (2.58)

 

    То же самое получается с формулами для определения работы:

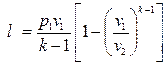
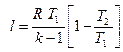
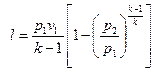
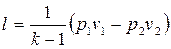
    Как и в любом другом процессе изменения состояния идеального газа изменение внутренней энергии определяется уравнением

.

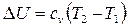    В связи с тем, что в адиабатном процессе запрещен теплообмен с окружающей средой, уравнение первого начала термодинамики принимает вид:

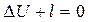
или

.

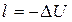    Иначе говоря, в адиабатном процессе работа расширения совершается за счет внутренней энергии системы. Наоборот, при сжатии вся затраченная на сжатие работа расходуется на увеличение внутренней энергии. По этой причине температура системы при адиабатном расширении падает, а при сжатии - возрастает.

 

Таблица 2.1

Сводная таблица частных случаев политропного процесса

 

Процесс	n	Соотношения параметров	DU	Dh	DS	q	l
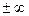
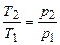
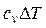
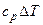
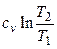
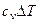
Изохорный v = const							0
Изобарный P = const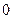
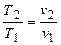
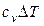
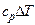
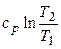
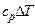
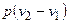
Изотермический T = const	1		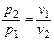0	0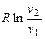
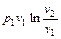
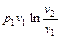
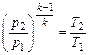
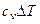
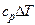
Адиабатный dq = 0	k				0	0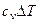

 

 

Рис. 2.3.

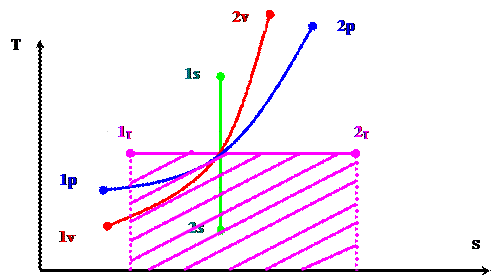
Рис. 2.4.

ЛЕКЦИЯ 5

 

СЖАТИЕ ГАЗОВ В КОМПРЕССОРАХ

 

Сжатый воздух находит широкое применение в различных отраслях техники.

Машины, применяемые для сжатия газа, называются компрессорами.

По способу сжатия газа компрессоры разделяются на две группы.

К первой группе относятся компрессоры статического действия или объемные компрессоры (поршневые, шестеренчатые, ротационные). Повышение давления в них достигается путем уменьшения объема газа, поступившего в рабочее пространство компрессора.

Ко второй группе относятся компрессоры динамического действия. К ним относятся центробежные, осевые и диагональные компрессоры. В этой группе компрессоров сжатие осуществляется в два этапа. В начале газ приобретает некоторый запас кинетической энергии, затем происходит преобразование кинетической энергии в потенциальную (энергию давления).

Несмотря на конструктивные различия указанных типов компрессоров, процессы сжатия газа в них с точки зрения термодинамики одинаковы.

Дальнейший анализ проводится применительно к поршневому компрессору.

На рис.1 в координатах P-V (V - объем газа в цилиндре при различных положениях поршня) представлена индикаторная диаграмма процесса сжатия газа в одноступенчатом компрессоре и под ней схема компрессора.

 

Рис. 1.

 

Принцип работы компрессора заключается в следующем. При ходе поршня из верхней мертвой точки (ВМТ) к нижней мертвой точке (НМТ) в цилиндр засасывается газ (процесс 4-1), который при обратном ходе поршня сначала сжимается (процесс 1-2), а потом выталкивается в газосборник (процесс 2-3). В крышке цилиндра компрессора располагаются впускной и выпускной клапаны, работающие под действием перепада давлений.

При засасывании газа (воздуха) впускной клапан открыт, а выпускной закрыт. В процессе сжатия воздуха, продолжающегося на части обратного хода поршня, оба клапана закрыты. По окончании процесса сжатия выпускной клапан открывается (точка 2), а поршень на оставшейся части пути до верхней мертвой точки выталкивает сжатый газ в газосборник.

Так как процессы 4-1 и 2-3 не являются термодинамическими то есть идут с неизменными термодинамическими параметрами (меняется лишь масса газа в цилиндре), то совокупность процессов, изображенных на рис.1, строго говоря, не является замкнутым термодинамическим циклом. Однако для удобства анализа эту диаграмму рассматривают как цикл идеального компрессора. Линия сжатия, в зависимости от количества отводимого от газа тепла (интенсивности охлаждения цилиндра охлаждающей жидкостью или воздухом), может быть изотермой 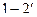, адиабатой 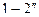, или политропой 1-2. В диаграмме T-S эти процессы изображены на рис.2.

 

 

Рис. 2.

 

Работа компрессора.

 

Работа, затрачиваемая на получение 1кг сжатого газа в одноступенчатом компрессоре, графически изображается площадью 4-1-2-3 (рис.1), которая является алгебраической суммой площадей:

 

F₄₁₂₃ = F₂₃₅₆ + F₁₂₆₇ - F₄₁₇₅ ,

где F₂₃₅₆ = l₁ = P₂V₂ - работа нагнетания;

    F₁₂₆₇ = l₂ = 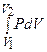 - работа сжатия;

    F₄₁₇₅ = l₃ = P₁V₁ - работа наполнения (отрицательная, потому что при   всасывании газ сам совершает работу над поршнем).

В соответствии с таким обозначением суммарная работа будет равна:

 

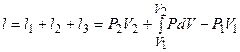                             (1)

 

В этом выражении 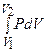 зависит от характера процесса сжатия.

1. При изотермическом сжатии:

 

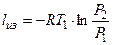                                      (1а)

 

2. В случае политропного сжатия:

 

 

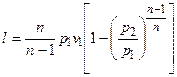                             (1б)

 

n – показатель политропы.

 

3. При адиабатном сжатии:

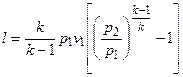                             (1в)

k - показатель адиабаты.

 

Вычисленная таким образом величина работы используется при определении энергетических затрат, необходимых для получения определенного количества газа при заданных параметрах начала и конца сжатия.

Как следует из рис.1 и сопоставления формул (1а), (1б) и (1в), наименьшая суммарная работа затрачивается при изотермическом сжатии газа. Кроме того, вследствие постоянства температуры в этом процессе создаются благоприятные условия для смазки.

 

В действительных компрессорах получить изотермическое сжатие практически невозможно, однако, стремятся максимально приблизиться к нему (вести процесс сжатия с показателем политропы 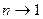). Поэтому при определении эффективности охлаждаемых поршневых компрессоров величина действительной работы сравнивается с изотермической. Отношение их дает изотермический КПД ( ).

 

 

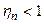Рис. 3.

 

Объемный КПД компрессора.

Отношение действительного объема всасывания ( 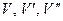) к рабочему объему цилиндра V_h называется объемным КПД:

 

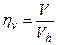                                                 (2)

 

а отношение 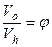 - относительной величиной “вредного пространства” (f = 0,01-0,03).

 

Очевидно, что с увеличением объема вредного пространства (V_o), будет уменьшаться действительный объем всасывания и объемный КПД, а следовательно, и производительность компрессора. На объемный КПД в значительной степени оказывает влияние величина конечного давления сжатия. Как следует из рис. 3, его увеличение (точки 2’, 2”, ..) уменьшает объемный КПД. В пределе, когда кривая процесса сжатия (линия 1-2) пересечет линию вредного пространства, всасывание газа в цилиндр компрессора прекратится, и будет повторяться сжатие и расширение одного и того же объема (объемный КПД h_v = 0).

 

Рис. 4.

 

Приведенный выше анализ показывает, что одноступенчатый поршневой компрессор не может быть применен для получения сжатого газа высокого давления вследствие уменьшения производительности с увеличением конечного давления и ухудшения условий смазки при этом (возможно самовоспламенение смазки при недостаточном охлаждении). Пределом для одноступенчатого компрессора обычно является давление конца сжатия в 10 – 12 ата.

 

ЛЕКЦИЯ 6

 

ИСТЕЧЕНИЕ ГАЗОВ И ПАРОВ

 

Суживающееся сопло

Анализ уравнения (15) позволяет перейти к выводу о том, что при заданных 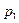,  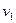и 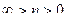 (область существования устойчивых равновесных состояний) величина массового секундного расхода зависит от значения выражения, взятого в квадратные скобки. Легко видеть, что при  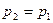(рис. 2) 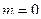. При 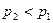 расход газа за счет увеличения расширения газа на участке 1-1 2-2 растет. Однако, при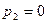 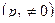 m снова становится равным нулю. Поскольку функция (15), будучи непрерывной, дважды проходит через ноль, то должен существовать максимум массового секундного расхода (рис. 3).

 

 

Величина соотношения 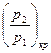, отвечающая  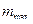найдется, если взять первую производную от выражения в квадратных скобках уравнения (15) и приравнять ее нулю.

В результате получаем, что для адиабатного процесса изменения состояния критический перепад давлений равен

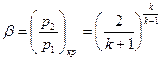.                                   (16)

 

Естественно, что при подстановке в уравнение (15) вместо 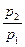 критического перепада давлений мы получим максимальную величину массового секундного расхода. Например, для адиабатного течения, которое чаще всего рассматривается в технических приложениях, имеем

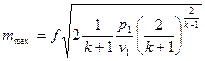.                                     (17)

 

При дальнейшем уменьшении давления, в окружающей среде 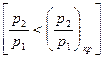 расход остается постоянным, равным 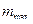. Это явление получило название "кризис течения".

 

Скорость течения газа при  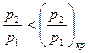также остается постоянной. Эта скорость называется критической скоростью течения 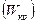. Уравнение для определения  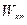может быть получено, если в (14) вместо  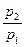ввести критический перепад давлений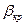

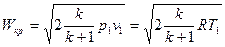.                                (18)

 

Разберем физическую картину процесса. По мере движения газа по каналу происходит его расширение, при котором уменьшается 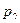 и .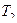

Снижение 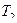 приводит к уменьшению местной скорости звука (9), а скорость потока возрастает. В выходном сечении канала скорость звука в соответствии с (9) будет равна

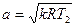.                                              (19)

 

При кризисе течения скорость потока в выходном сечении определяется (18). Введем в это уравнение вместо 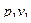 температуру Т. Для адиабатного процесса при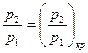

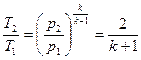
или

.

 

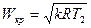Таким образом, при достижении критического перепада давлений на выходе из суживающегося сопла скорость потока достигает местной скорости звука. Между тем, давление распространяется тоже со скоростью звука. В результате, уменьшение в окружающей среде давления ниже 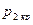 не может подойти к устью сопла, и в последнем устанавливается постоянное давление, равное  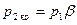(19). Этим объясняется тот факт, что при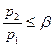

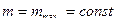
и

.

 

 

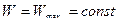Сопло Лаваля

Проведенный анализ касался течения газа через суживающееся сопло. Из него не следует делать вывод о том, что вообще не возможно, например, при адиабатном течении получить скорость потока выше звуковой.

 

Как следует из уравнения (10.1), для перехода в область сверхзвуковых скоростей необходимо иметь расширяющийся канал. Следовательно, дополняя суживающийса канал, где газ достигает критической скорости, расширяющимся, мы предоставляем газу возможность продолжить свое расширение и приобрести сверхзвуковую скорость. Такое комбинированное сопло называется соплом Лаваля (рис. 4).

 

Сопло Лаваля целесообразно применять лишь при 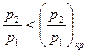. Скорость истечения, например, при адиабатном течении определится с помощью уравнения (14). Расход определится по минимальному сечению, где имеет место кризис течения. Для этого используется уравнение для определения 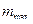, в которое следует подставлять вместо f минимальное сечение сопла f_min.

ЛЕКЦИЯ 7

 

РЕАЛЬНЫЕ ГАЗЫ

 

В ряде случаев приходится иметь дело с системами, состояние которых не позволяет использовать модель идеального газа. В качестве примера можно назвать водяной пар в тех состояниях, при которых он используется в паросиловых установках.

 

Здесь приходится принимать во внимание, что молекулы имеют определенные размеры и между ними существуют силы взаимодействия: притяжение при сравнительно больших расстояниях между молекулами и отталкивание при сближении молекул на малые расстояния.

 

Модель реального газа представляется в виде твердых шариков диаметром d₀, взаимно притягивающихся друг к другу.

 

Как видно, модель реального газа отличается от модели идеального газа, во-первых, тем, что сами молекулы имеют некоторый объем, во-вторых, наличием сил межмолекулярного сцепления.

 

В общем случае, это приводит к тому, что в отличие от идеального газа

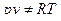
и при T = const

.

 

 

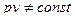Области pv- диаграммы

 

1. Область левее нижней пограничной кривой KI – это область некипящей жидкости.

 

2. Линия KI - это геометрическое место точек начала парообразования или конца конденсации. Иначе эту линию называют нижняя пограничная кривая. Степень сухости на нижней пограничной кривой равняется нулю (x = 0), а состояние вещества  кипящая жидкость.

 

3. Область между KI и KII - область влажного насыщенного пара.

Это смесь сухого насыщенного пара с каплями жидкости (туманообразное состояние). Это двухфазное состояние.

 

Для того чтобы превратить 1 кг жидкости в пар, надо сообщить ей какое-то количество теплоты. Эту величину называют удельной теплотой парообразования r, кДж/кг.

 

4. Линия KII - это геометрическое место точек конца парообразования или начала конденсации. Линию KII иначе называют верхняя пограничная кривая. Степень сухости на верхней пограничной кривой равняется единице (x = 1), а состояние вещества сухой насыщенный пар.

 

Насыщенный пар - это пар, находящийся в динамическом равновесии с жидкостью.

 

5. Точка К - критическая точка.

 

6. Область правее и выше верхней пограничной кривой – это область перегретого пара.

 

 

Таблицы водяного пара

 

Имеются три таблицы водяного пара. В двух из них приведены параметры кипящей воды и сухого насыщенного пара, т.е. параметры, характеризующие состояния пара на нижней и верхней пограничных кривых.

 

Таблица 1

 

Рн	Тн	v’	v’’	h’	h’’	r	s’	s’’
бар	0 С	м3/с	м3/с	кДж/кг	кДж/кг	кДж/кг	кДж/кг К	кДж/кг К

 

Таблица 2

 

Тн	Рн	v’	v’’	h’	h’’	r	s’	s’’
0 С	бар	м3/с	м3/с	кДж/кг	кДж/кг	кДж/кг	кДж/кг К	кДж/кг К

 

 

В таблице 1 приведены указанные выше параметры в функции от давления кипения (насыщения), в таблице 2 – от температуры кипения (насыщения). В этих таблицах приводятся удельные объемы кипения воды (v’) и сухого насыщенного пара (v’’), соответственно их энтальпия (h’, h’’) и энтропия (s’, s’’). Кроме того, в этих таблицах приводится значение скрытой теплоты парообразования (h’’- h’ = r).

 

Таблица 3

 

Р / Т	0	10	20	30	40
0,01	V  h  s
0,02	V h  s		пар
0,03	V  h  s	жидкость
0,04

 

В таблице 3 приведены в функции Р и Т значения v , h и s для воды, не нагретой до кипения, и для перегретого пара.

 

Таким образом, таблицами не охватывается область влажного насыщенного пара, параметры состояния которого определяются путем расчета с использованием таблиц 1 и 2.

 

Диаграммы водяного пара

 

В инженерной практике для определения параметров состояния и анализа процессов используются не только таблицы водяного пара, но и соответствующие диаграммы.

Наиболее распространены T-S - и особенно i-S - диаграммы.

 

TS - диаграмма (рис. 2) используется для процессов парообразования и конденсации. Это тепловая диаграмма.

 

Площадь S_a  a b S_b - теплота парообразования.

 

hS - диаграмма (рис. 3).

 

Расчет процессов изменения состояния реального газа (водяного пара) (рис. 3).

 

1. Изохорный процесс (V = const) 1_v - а_v - 2_v .

 

1_v - а_v - изохорная подсушка влажного насыщенного пара. В ходе этого степень сухости (х = 1) т.е. вся жидкая фаза превращается в парообразную.

Происходит увеличение температуры, давления, энтальпии и энтропии.

 

а_v - 2_v - изохорный перегрев пара (происходит увеличение температуры, давления, энтальпии и энтропии).

 

U_1-2 = h₂ - h₁ -  V(p₂ - p₁)

 

l = 0 - работа расширения

 

q_1-2 = DU_1-2

 

2. Изобарный процесс (p = const) 1_р - а_р  - 2_р .

 

1_р - а_р - изобарная подсушка влажного насыщенного пара. В ходе этого степень сухости (х = 1) т.е. вся жидкая фаза превращается в парообразную.

Происходит увеличение энтальпии и энтропии при Р = const; T = const.

 

а_р - 2_р - изобарный перегрев пара (происходит увеличение температуры, энтальпии и энтропии при Р = const).

 

U_1-2 = h₂ - h₁ -  p(V₂ - V₁)

 

l = p (V₂ - V₁ ) – работа расширения

 

q_1-2 = h₂ - h₁

 

3. Изотермический процесс (Т = const) 1_т - а_т - 2_т .

 

1_т - а_т - изобарно - изотермическая подсушка влажного насыщенного пара. В ходе этого степень сухости (х = 1) т.е. вся жидкая фаза превращается в парообразную. Происходит увеличение энтальпии и энтропии при Р = const;

T = const (В идеальном газе при T = const - h = const , S = const).

 

В реальном газе учитывается потенциальная энергия межмолекулярных связей, поэтому происходит увеличение энтальпии и энтропии.

 

а_т - 2_т - изотермический перегрев пара (при T = const происходит увеличение энтальпии энтропии и внутренней энергии, уменьшается давление).

 

U_1-2 = h₂ - h₁ - ( p₂V₂ - p₁V₁)

 

l = q - DU

 

q_1-2 = T(S₂ -S₁)

 

4. Адиабатный процесс (q = 0) 1_s - 2_s .

 

1_s - 2_s - адиабатное расширение.

При S = const понижается энтальпия, температура и давление.

 

DU = h₂ - h₁ - ( p₂V₂ - p₁V₁)

 

l = DU

 

q_1-2 = 0

 

DS = 0

 

 

ЛЕКЦИЯ 8

 

ТЕПЛООБМЕН И ТЕПЛОПЕРЕДАЧА

 

Этим названием определяется содержание того раздела курса, к которому мы сейчас приступаем. Наша задача будет заключаться в том, чтобы познакомиться с основами учения о процессах передачи и распространения тепла.

Знание законов теплопередачи имеет решающее значение при проектировании и эксплуатации большого числа устройств и сооружений практически во всех отраслях промышленности.

Теплообменом называются процессы переноса тепла в пространстве.

Теплообмен – сложное явление, которое может быть разделено на три частных способа передачи тепла: теплопроводность, конвекцию и тепловое излучение.

Рассмотрим краткую характеристику каждого из указанных способов.

 

ТЕПЛОПРОВОДНОСТЬ

 

Теплопроводность – процесс передачи энергии за счет непосредственного взаимодействия микрочастиц вещества.

Теплопроводность представляет собой передачу кинетической энергии от одних молекул к другим. В чистом виде теплопроводность встречается в твердых телах. В таких телах, как стекло и кварц, часть энергии наряду с теплопроводностью передается излучением. В газах и жидкостях передача тепла теплопроводностью дополняется передачей конвекцией и излучением. В аморфных веществах теплота передается за счет упругих волн в материале. В проводниках – за счет диффузии свободных электронов. В подвижных средах – за счет соударения молекул.

 

ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ

 

Тепловой поток Q 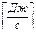 [Вт] – это количество теплоты, проходящее в единицу времени через поверхность, перпендикулярную температурному градиенту.

Удельный тепловой поток или плотность теплового потока:

 

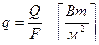
Температурное поле – совокупность всех значений температуры в теле в данный момент времени.

Процесс теплопроводности (как и другие виды теплообмена) может иметь место лишь тогда, когда в различных точках тела температура неодинакова. В общем случае процесс передачи тепла теплопроводностью в твердом теле сопровождается изменением температуры как в пространстве, так и во времени.

Значение температуры в любой точке пространства, определяемой координатами x , y , z в каждый момент времени τ может быть описано уравнением:

 

 

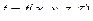
которое представляет собой математическое выражение температурного поля в его наиболее общем виде, когда температура меняется вдоль всех координатных осей, а также с течением времени. Такое температурное поле называют трехмерным нестационарным.

 

 Если 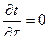, т.е. температура каждой точки с течением времени не изменяется, то такое поле называется трехмерным стационарным.

Режим называется установившимся или стационарным.

 

 

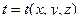
Наиболее простым является случай одномерного температурного поля:

 

 

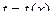
когда температура с течением времени не изменяется и является функцией лишь одной координаты.

 

Целью решения задач является определение температурного поля.

 

Изотермическая поверхность – это геометрическое место точек с одинаковой температурой.

 

Свойства изотермических поверхностей:

1. В однородном изотропном теле изотермические поверхности непрерывны;

2. Изотермические поверхности не пересекаются.

 

Для того, чтобы оценить, насколько резко меняется температура внутри тела, пользуются понятием температурного градиента:

 

 

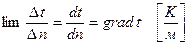
Температурный градиент – предел отношения разности температур между изотермами к расстоянию между ними по нормали при стремлении этого расстояния к нулю.

Температурный градиент - величина векторная, положительное направление которой совпадает с направлением роста температуры.

Тепловой поток передается в обратном направлении.

 

 

ОСНОВНОЙ ЗАКОН ТЕПЛООТДАЧИ.

ЛЕКЦИЯ 9

 

Граничные условия.

· Граничными условиями первого рода задается закон распределения температуры по поверхности объекта в любой точке поверхности и в любой момент времени.

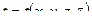
· Граничные условия второго рода – определяют значения плотности теплового потока на поверхности объекта в любой точке и в любой момент времени.

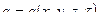
· Граничные условия третьего рода – определяют температуру жидкости омывающей поверхность или закон ее изменения и условия теплообмена на границах раздела сред. Должна быть задана температура и вид теплообмена (t _ж , t_c, a …).

· Граничные условия четвертого рода – условия на границе раздела двух твердых тел. Теплота, подведенная к поверхности одного тела, передается полностью другому телу, имеющему другие характеристики.

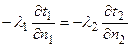
Совокупность дифференциального уравнения теплопроводности и условия однозначности представляют собой полную математическую формулировку задачи.

 

 

Рассмотрим пример.

ЛЕКЦИЯ 1

ОРГАНИЧЕСКИЕ ТОПЛИВА

 

Топлива – это природные вещества которые экономически целесообразно использовать для получения теплоты в больших количествах. Различают химические и ядерные топлива. Мы будем рассматривать только химические органические топлива, применяемые в промышленности и энергетике.

Топливо представляет собой совокупность горючего и окислителя.

К горючим относят водород (Н₂); щелочные металлы: натрий (Na), магний (Mg), алюминий (Al), калий (K); углерод (С) и углеводородные соединения.

К окислителям относят кислород (О₂), соединения с кислородом и элементы гомогенного ряда: фтор (F), хлор (Cl).

        

В таблице 1.1 приведена классификация углеводородных горючих по происхождению и агрегатному состоянию.

 

Таблица 1.1

Классификация углеводородных горючих

 

Происхождение Агрегатное состояние	Природные	Искусственные
Твердое	древесина, торф, бурый уголь, каменный уголь, полуантрацит, антрацит, горючие сланцы	кокс, древесный уголь, брикеты
Жидкое	нефть, газовый конденсат        (белая нефть)	продукты переработки нефти: бензин, лигроин, керосин, соляровое масло (газойль), мазут; спирты
Газообразное	природный газ, попутный газ	генераторные газы, газы сухой перегонки, доменный и коксовый газы, светильный газ, биогаз

 

Состав топлив

 

    Свойства топлив, целесообразность их использования в значительной мере определяются их химическим составом, который для жидких и твердых топлив задается обычно в процентах по массе. Состав газового топлива задается объемным содержанием в % входящих в него газов.

    Элементы, входящие в состав топлива, обозначаются соответствующими символами: С – углерод; Н – водород; О – кислород; N – азот; S – сера. Зола и влага, входящие в состав топлива, обозначаются соответственно А и W.

    Влажность и зольность топлив даже в пределах одного сорта подвержены значительным колебаниям, поэтому для уточнения характеристик вводятся понятия о горючей, сухой и рабочей массах топлива. Обратите внимание на различия уравнений материального баланса для этих случаев.

    Материальный баланс горючей  массы углеводородного топлива

C_г + H_г + O_г+ N_г + S_г = 100 %.

Материальный баланс сухой массы:

С_c + H_c + O_c + N_c + S_c + A_c = 100 %.

 

Материальный баланс рабочей массы

С_p + H_p + O_p + N_p + S_p + A_p + W_p = 100 %.

Совокупность золы и влаги, входящих в состав топлива, называют внешним балластом горючего. Совокупность кислорода и азота, входящих в состав топлива, называют  внутренним балластом горючего.

 

Характеристики топлив

    К основным характеристикам, определяющих ценность топлив, относят следующие.

1. Вязкость.

2. Температура воспламенения.

3. Температура вспышки.

4. Токсичность.

5. Температура замерзания.

6. Температура перегонки.

7. Запыленность (для газообразных горючих).

8. Теплота сгорания Q, Дж – это количество теплоты, выделяющейся при полном сгорании горючего.

 

Для инженерных расчетов процессов горения пользуются понятием - удельная теплота сгорания q , Дж/кг - это количество теплоты, выделяющейся при полном сгорании 1кг твердого (жидкого) или одного нормального кубического метра (1 нм³) газообразного горючего.

1 нм³ - это кубический метр при нормальных условиях (t = 0 ­­⁰C, Р = 760 мм. рт. ст.).

 

Принято различать высшую и низшую теплоту сгорания.

q_в = q_н +0,025 (9H_р + W_p), МДж / кг,

 

где q_в - высшая теплота сгорания – это количество теплоты, выделяющейся при сгорании топлива с учетом теплоты конденсации водяных паров, образующихся при сгорании водорода Н_р и испарении влаги W_p;

  q_н - низшая теплота сгорания – теплота сгорания топлива, при условии, что влага, образующаяся при сгорании водорода топлива 9Н_р и влага топлива W_p находятся в парообразном состоянии;

0,025 МДж/кг - теплота парообразования воды;

9Н_р – количество влаги, выделяющейся при полном сгорании рабочей массы водорода топлива;

W_р – количество влаги, которое содержится в горючем.

 

Самым калорийным горючим является - водород (Н₂).

 

q_н = 140 МДж/кг - для водорода;

q_н = 20-30 МДж/кг - для каменного угля;

q_н = 38 МДж/кг - для мазута.

 

Условное топливо - это такое эффективное, несуществующее в природе топливо, теплота сгорания которого

q_усл = 29,33 МДж/кг (7000 ккал/кг).

 

Условный эквивалент - это отношение низшей теплоты сгорания горючего к теплоте сгорания условного топлива:

В_усл = q_н/q_усл.

 

В России на гражданина приходится примерно около 2 тонн условного топлива в год. В развитых странах (США, Великобритания, Германия) на гражданина приходится примерно около 10 тонн условного топлива в год.

 

Разновидности горения

 

Горением называется химическая реакция взаимодействия горючего с окислителем, сопровождающаяся интенсивным выделением теплоты и резким повышением температуры.

Горение возможно только в газообразной фазе.

Если горючее и окислитель находятся в одной газообразной фазе, то горение называют гомогенным.

Если один из компонентов топлива находится в отличном от газообразного состояния, то горение называют гетерогенным.

При гетерогенном горении происходит изменение агрегатного состояния вещества.