Закон сохранения и превращения энергии является наиболее общим универсальным законом природы, применяемым ко всем явлениям и процессам.

Этот закон формулируется так:

Энергия изолированной системы, при любых происходящих в ней процессах, не меняется; энергия не уничтожается и не создается.

Первый закон термодинамики является частным случаем этого закона применительно к процессам, протекающим в термодинамических системах.

В соответствии с первым законом термодинамики внутренняя энергия термодинамической системы может изменяться лишь в результате энергетического обмена с окружающей средой.

В термодинамике первое начало обычно записывают так (применительно к 1кг массы):

q = Δu + l                                             (2.6)

или в дифференциальной форме:

dq = du + dl .                                          (2.7)

Таким образом, в общем случае тепло, подводимое к системе, расходуется как на изменение энергии, так и на совершение работы.

Работа 1 кг газа в элементарном равновесном процессе:

dl = pdv .                                                     (2.8)

Для конечного процесса:

l = 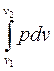.                   (2.9)

Чтобы решить интеграл (2.9), надо знать зависимость, связывающую давление и объем в ходе процесса. Таким образом, работа, производимая газом, в отличие от параметров состояния, зависит от вида процесса.

2.4. СВОЙСТВА р v – и Т s – ДИАГРАММ

Если воспользоваться системой координат р v, то величину работы можно определить графически.

Нетрудно видеть (рис. 2.1), что элементарная площадка аbcd = р dv = dl, а площадь АВС D = 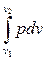= l . Таким образом, в системе координат рv работа, приведенная в ходе процесса численно равна площади, ограниченной кривой процесса, осью абсцисс и крайними ординатами.

Из-за этого свойства р v - диаграмму называют иногда рабочей диаграммой.

Теплота, подведенная (отведенная) в ходе элементарного обратимого процесса может быть, в частности, вычислена при использовании уравнений (2.4) и (2.5)

dQ = TdS    или dq = Tds .                                   (2.10)

Для всего процесса

Q = 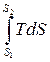 или q = 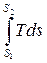.                                      (2.11)

    Взаимосвязь между Т и S в разных процессах различна. Поэтому количество теплоты (как и работы) зависит не только от начального и конечного состояний системы, но и от вида процесса.

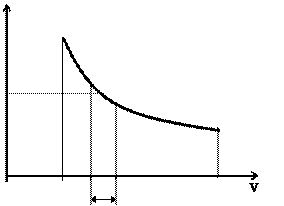
    Решение интегралов (2.11) можно осуществить графическим путем, если воспользоваться диаграммой Тs. Нетрудно видеть (рис. 2.2), что элементарная площадка аbcd = Tds = dq, a площадь АВСD = 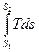 = q.

Таким образом, в системе координат Тs площадь, ограниченная кривой процесса, осью абсцисс и крайними ординатами численно равна подведенной (отведенной) теплоте. Поэтому Тs- диаграмму иначе называют тепловой.

Следует добавить, что по изменению энтропии в обратимых процессах можно сделать вывод, о направлении теплообмена.

Как следует из уравнений (2.10) знак dq и знак ds совпадают, т.к. абсолютная температура сугубо положительная величина.

Если рассмотреть совместно уравнения (2.7), (2.8) и (2.10), то уравнение первого начала может быть приведено к виду

Т ds = du + pdv .                                                (2.12)

Рис. 2.1.                                                                     Рис. 2.2.

Лекция 4