Найдем соотношения между параметрами состояния в политропном процессе.

Установим вначале взаимосвязь между давлением и объемом. Используя уравнение (2.22), получим

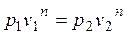
или

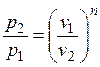.                                (2.23)

Из уравнения (2.23) следует, что при n > 0 изменение давления в политропном процессе обратно пропорционально изменению объема. При n < 0 – прямо пропорционально.

Для установления взаимосвязи между P и Т, V и Т знаменатель уравнения состояния для любых двух точек процесса:

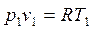 и .

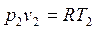После деления второго на первое получим:

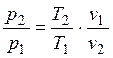.                             (2.24)

Подставляя это соотношение в (2.23) получим соотношение между Т и v

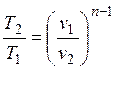.                             (2.25)

Таким образом, в политропных процессах при n > 1 изменение объема обратно пропорционально изменению абсолютной температуры. При n < 1 – прямо пропорционально.

Если с помощью (2.23) исключить из (2.24) объем, то получим соотношение между Т и p

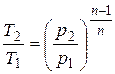.                          (2.26)

Как видно из (2.26), при n > 1 и n < 0 изменение давления прямо пропорционально изменению температуры. При 1 > n > 0 – обратно пропорционально.

Определение изменения внутренней энергии

Изменение внутренней энергии, как и любого другого параметра состояния, не зависит от характера процесса. В случае идеального газа оно всегда определяется с помощью следующих уравнений.

Для элементарного процесса

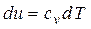.                                          (2.27)

Для 1 кг массы термодинамической системы

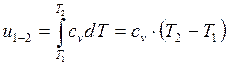.                        (2.28)

Для всей массы термодинамической системы

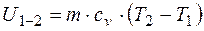.                    (2.29)

Определение изменения энтальпии

Для элементарного процесса

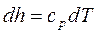.                                (2.30)

Для 1 кг массы термодинамической системы

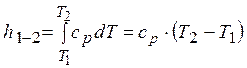.           (2.31)

Для всей массы термодинамической системы

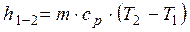.                       (2.32)

Определение изменения энтропии

Изменение энтропии в элементарном термодинамическом процессе по определению выражается соотношением

.

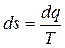Используя соотношение первого закона термодинамики (2.13), получим

.

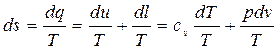Если решить уравнение состояния идеального газа, то получим 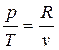, следовательно

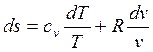 .                                       (2.33)

Интегрируя соотношение (2.33), получим изменение энтропии в конечном процессе для 1 кг термодинамической системы

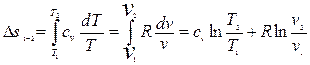.       (2.34)

Используя выражение первого закона термодинамики в форме (2.16), и проделав аналогичные преобразования, получим

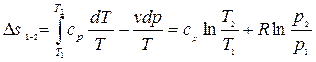.                (2.35)

Определение теплоты, подводимой (отводимой)

В ходе политропного процесса

Количество тепла, подводимого (отводимого) в ходе политропного процесса, можно определить с помощью уравнения первого закона термодинамики

.

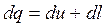Сказанное не исключает возможности определения dq с помощью теплоемкости

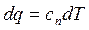
или

.

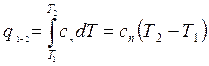Используя соотношение (2.19) найдем теплоемкость политропного процесса

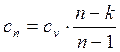,                                (2.36)

где 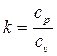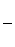показатель адиабаты.

Таким образом

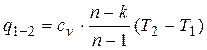.                             (2.37)