Во многих практических задачах модель закона распределения заранее неизвестна, поэтом возникает вопрос выбора модели, согласующейся с результатами наблюдения надс.в.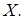

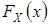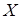Предположим, что неизвестная функция распределения с.в. имеет определенную модель 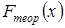, то есть сформулируем гипотезу 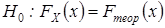. Тогда в качестве альтернативной выдвинем гипотезу 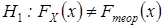. Требуется сделать вывод: согласуются ли данные наблюдений с высказанным предположением?

Определение 24.Критерием согласия называется критерий, с помощью которого проверяется гипотеза о предполагаемом виде закона распределения (о согласовании предполагаемого вида распределения с опытными данными на основании выборки).

Критерий 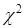 Пирсона

Для проверки гипотезы 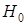 поступим следующим образом. Разобъем всю область значений с.в.  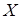на 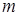 интервалов  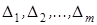и подсчитаем вероятности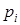 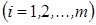 попадания с.в.  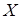в интервал  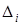по формуле

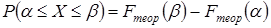
(26)

Тогда теоретическое число значений с.в. X, попавших в интервал 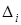, можно вычислить по формуле

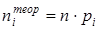
(27)

Таким образом, получим вариационный ряд распределения и теоретический ряд распределения. Если эмпирические частоты сильно отличаются от теоретических, то проверяемую гипотезу 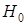 отвергаем, в противном случае – принимаем ее.

В качестве критерия, характеризующего степень расхождения между эмпирическими и теоретическими частотами, К.Пирсон предложил статистику

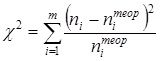
(28)

При 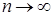 эта величина имеет 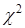– распределение с  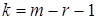степенями свободы, где 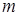– число интервалов выборки, 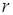– число параметров предполагаемого распределения. Например, в случае нормального распределения оценивают два параметра  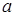и 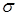, поэтому .

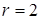Схема применения критерия 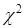 Пирсона сводится к следующему:

1. По формуле (41) вычисляем 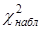– выборочное значение статистики критерия.

2. Задав уровень значимости 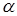 критерия, по таблице 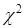– распределения находим критическую точку (квантиль) .

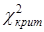3. Если 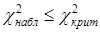, то гипотеза  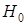не противоречит данным наблюдений; в противном случае если 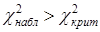, гипотезу  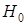отвергаем.

Необходимым условием применения критерия 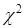 Пирсона является выполнение соотношения 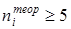. Если для какой-то группы выборки оно не выполняется, такую группу объединяют с соседней и соответственно уменьшают число групп.

Критерий Колмогорова

Критерий Колмогорова является наиболее простым критерием проверки гипотезы о модели закона распределения. Он связывает эмпирическую функцию распределения 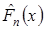 с функцией распределения  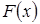непрерывной с.в. .

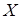Рассмотрим 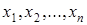– конкретную выборку из распределения с неизвестной функцией распределения 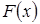. Пусть 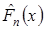–эмпирическая функция распределения. Сформулируем простую гипотезу 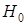: 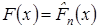, в качестве альтернативной выдвинем гипотезу : .

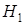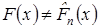Согласно критерию Колмогорова вводится в рассмотрение функция

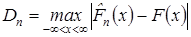
(29)

Эта функция называется статистикой Колмогорова и представляет собой максимальное отклонение эмпирической функции распределения 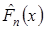 от гипотетической (теоретической) функции распределения .

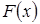Колмогоров доказал, что при 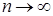 закон распределения с.в.  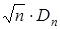стремится к закону распределенияКолмогорова независимо от вида распределения с.в. 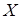, то есть

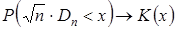
(30)

где 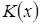– функция распределенияКолмогорова. Для нее составлена таблица значений, которой можно пользоваться при :

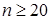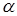
	0,1	0,05	0,02	0,01	0,001
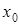
	1,224	1,358	1,520	1,627	1,950

Найдем такое значение 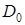, при котором выполняется равенство

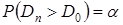
(31)

Рассмотрим уравнение 

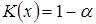
(32)

С помощью функции распределенияКолмогорова найдем корень 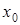 этого уравнения, тогда

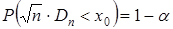
(33)

Следовательно, вероятность

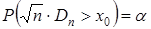
(34)

Таким образом,

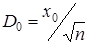
(35)

 Если 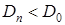, то гипотеза  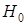принимается, в противном случае гипотеза  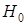отвергается.