Одним из часто встречающихся применений статистических методов на практике является решение вопроса о том, должно ли быть принято или отвергнуто предположение (гипотеза) относительно генеральной совокупности (случайной величины) на основании данной выборки. Например, новое правило поступления в вуз испытано на определенном числе абитуриентов. Логично выяснить, можно ли сделать обоснованный вывод о его эффективности по сравнению с предыдущим правилом поступления по данным результатам?

Определение 22 .Статистической гипотезой называется любое высказывание (предположение) о генеральной совокупности, проверяемое по выборке (по результатам наблюдений).

Определение 23 .Проверкой гипотезы называется процедура сопоставления высказанного предположения (гипотезы) с выборочными данными.

Статистические гипотезы делятся на параметрические (гипотезы о параметрах распределения известного вида) и непараметрические (о виде неизвестного распределения).

Основываясь на выборочных данных и учитывая условия конкретной задачи, выдвигают гипотезу 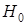 в качестве основной (нулевой), а другую гипотезу 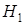, являющуюся ее логическим отрицанием, – в качестве конкурирующей (альтернативной). Например, если нулевая гипотеза состоит в том, что математическое ожидание равно 10 ( 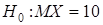), то в качестве альтернативной можно рассматривать одну из следующих гипотез: .

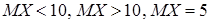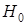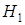Имея две гипотезы  и , надо на основе выборки 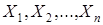принять либо нулевую гипотезу 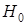, либо альтернативную гипотезу 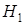. Правило, согласно которому принимается или отклоняется гипотеза 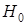, называется критерием проверки гипотезы .

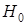При проверке гипотезы может быть принято неправильное решение, то есть, допущены ошибки 1-го и 2-го рода. Ошибка 1-го рода состоит в том, что отвергается нулевая гипотеза 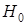, когда на самом деле она верна. Вероятность ошибки 1-го рода называется уровнем значимости критерия и обозначается через 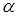. Ошибка 2-го рода состоит в том, что принимается нулевая гипотеза 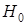, когда на самом деле верна гипотеза 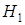. Вероятность ошибки 2-го рода обозначается через 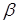. Величина  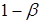называется мощностью критерия. Обобщим сказанное в виде таблицы.

Гипотеза	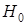Отвергается	Принимается
верна	Ошибка 1-го рода, ее вероятность равна	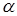Правильное решение, его вероятность равна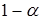
неверна	Правильное решение, его вероятность равна	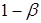Ошибка 2-го рода, ее вероятность равна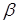

Схема проверки гипотез сводится к следующему:

Этап 1. Располагая выборкой 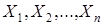, формулируют нулевую гипотезу  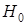и альтернативную .

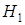Этап 2. В каждом конкретном случае подбирают статистику критерия 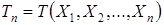 (функцию выборки, формирующуюся на основании результатов выборки 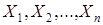), обычно из перечисленных ниже: U–нормальное распределение, 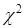- распределение Пирсона, t–распределение Стьюдента, F – распределение Фишера – Снедекора.

Этап 3. По статистике критерия 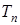 и заданному уровню значимости  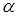определяют критическую область S (и 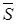). Для ее отыскания достаточно найти критическую точку 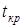, то есть границу, отделяющую область S от 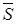. Границы областей определяются из соотношений:

· для правосторонней критической области: .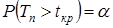

· для левосторонней критической области: .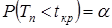

· для двусторонней критической области: .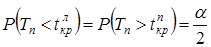

Для каждой области по соответствующим таблицам находят критическую точку, удовлетворяющую приведенным соотношениям.

Этап 4.Для полученной реализации выборки 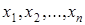 вычисляют значение критерия .

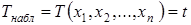Этап 5. Если 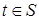, то нулевую гипотезу  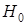отвергают и принимают альтернативную 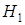; если же 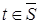, то нулевую гипотезу  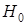принимают.