Предположим, что мы изучаем некоторуюс.в.X и с этой целью производим ряд независимых наблюдений. Пусть X приняла  раз значение, равное ,  раз – значениеx₂,…, n_k раз – значение x_k, при этом ,где  – объем выборки.

Определение 6.Вариантами с. в. 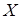 называются значения .

Определение 7.Частотами называются числа , которые показывают, сколько раз встречаются значения  в ряде наблюдений.

.

(1)

Определение 8.Относительными частотами называются отношение частот  к объему выборки :

Определение 9.Распределением выборки или вариационным рядом называется ранжированный (упорядоченный) перечень вариантов  и соответствующих им частот . Вариационный ряд называется дискретным, если любые его варианты отличаются на постоянную величину, и интервальным, если варианты могут отличаться один от другого на сколь угодно малую величину.

Для построения интервального ряда необходимо определить величину частичных интервалов, на которые разбивается весь интервал варьирования наблюдаемых значений с.в. 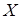. Длину частичного интервала  нужно выбрать таким образом, чтобы построенный ряд, с одной стороны, не был громоздким, а с другой стороны, позволял выявить характерные черты изменения изучаемой с.в.X.По формуле Стерджеса оптимальное число интервалов определяется по формуле:

,а длина интервала –

,

(2)

где – разность между наибольшим и наименьшим наблюдаемыми значениями, при этом за начало первого интервала принимается .

Пример 2. В результате трех экзаменов группа из 30 наудачу выбранных абитуриентов набрала следующую сумму баллов: 157, 175, 170, 166, 159, 173, 182, 167, 171, 169, 172, 164, 173, 175, 171, 158, 179, 156, 165, 179, 155, 178, 160, 154, 183, 153, 155, 167, 186, 163. Построить интервальный ряд.

Решение . Сначала упорядочим полученные данные по возрастанию:

153, 154, 155, 155, 156, 157, 158, 159, 160, 163, 164, 165, 166, 167, 167, 169, 170, 171, 171, 172, 173, 173, 175, 175, 178, 179, 179, 182, 183, 186.

Ясно, что 153, 186. Найдем число частичных интервалов и длину интервала по формуле Стерджеса: , 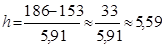. Возьмем h=6, тогда x _нач=153-0,5×6=150. Разобьем весь ряд на 6 интервалов: [150, 156),
[156, 162), [162, 168), [168, 174), [174, 180), [180, 186).Подсчитаем число абитуриентов, попавших в каждый из полученных интервалов, и получим интервальный ряд:

Сумма баллов	[150, 156)	[156, 162)	[162, 168)	[168, 174)	[174, 180)	[180, 186)
Частота	4	5	6	7	5	3
Относит.частота

Определение 10 .Функция

(3)

называется эмпирической функцией распределения, где n – объём выборки, n_k– частота появления варианты x_k, а – число выборочных значений <x .

Эмпирическая функция распределения по её вариационному ряду строится так:

(4)

Значениями  являются так называемые накопленные частости. График эмпирической функции распределения строят так же, как и график функции распреде­ления  дискретной с.в.

Если вариационный ряд составлен по интервалам значений и в качестве представителя интервала берется его середина, то эмпи­рическая функция составляется так же, как по вариационному ряду по значениям. Но в качестве представителя интервала можно брать правый конец интервала. Объединяя отрезками точки, ко­ординатами которых являются правые концы интервалов и накоп­ленные частости соответствующих интервалов, получаем ломаную линию, являющуюся довольно хорошим приближением графика функции распределения непрерывной случайной величины. Такой график является точным, если все значения в каждом интервале распределены равномерно. Аналитический вид этой функции довольно сложен.

В отличие от эмпирической функции распределения  функцию распределения  генеральной совокупности называют теоретической функцией распределения. Функция  играет фундаментальную роль в математической статистике. Важнейшее её свойство состоит в том, что при увеличении объёма выборки п  происходит сближение этой функции с теоретической.

Полигон и гистограмма

Наблюдаемые данные, представленные в виде вариационного ряда, можно изобразить графически с помощью полигона и гистограммы. Это позволяет получить наглядное представление о закономерности варьирования наблюдаемых значений с.в. X.

Определение 11.Полигоном частот(относительных частот) называется ломаная, отрезки которой соединяют точки с координатами ; ;…;  (с координатами ; ; … ; ).

Определение 12.Гистограммой частот (относительных частот) называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы длиной , а высоты равны частотам (относительным частотам) соответствующих интервалов.

Пример 3. Для оценивания знаний студентов-первокурсников проведена контрольная работа по высшей математике. Результаты контроля в выбранной группе из 25 студентов оказались следующими: 3 студента выполнили работу на «5», 10 студентов – на «4», 9 студентов – на «3» и 3 студента – на «2». Построить полигон частот и эмпирическую функцию распределения.

Решение. Объём выборки n=25. Представим исходные данные в виде дискретного вариационного ряда:

   □

Лекция 2