Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Лекции по математической статистике

 

Лекция 1

Полигон и гистограмма

Наблюдаемые данные, представленные в виде вариационного ряда, можно изобразить графически с помощью полигона и гистограммы. Это позволяет получить наглядное представление о закономерности варьирования наблюдаемых значений с.в. X.

Определение 11.Полигоном частот(относительных частот) называется ломаная, отрезки которой соединяют точки с координатами ; ;…;  (с координатами ; ; … ; ).

Определение 12.Гистограммой частот (относительных частот) называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых являются частичные интервалы длиной , а высоты равны частотам (относительным частотам) соответствующих интервалов.

Пример 3. Для оценивания знаний студентов-первокурсников проведена контрольная работа по высшей математике. Результаты контроля в выбранной группе из 25 студентов оказались следующими: 3 студента выполнили работу на «5», 10 студентов – на «4», 9 студентов – на «3» и 3 студента – на «2». Построить полигон частот и эмпирическую функцию распределения.

xk	2	3	4	5
nk	3	9	10	3

Решение. Объём выборки n=25. Представим исходные данные в виде дискретного вариационного ряда:

 

Построим полигон частот:

Согласно формуле (16)эмпирическая функция распределения

   □

 

Лекция 2

 

Лекция 3

Интервальные оценки параметров распределения

Точечные оценки неизвестного параметра q хороши в качестве первоначальных результатов обработки наблюдений. Их недостаток состоит в том, что неизвестна точность 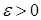 оценивания параметра. Поэтому и возникает задача о приближении параметра q не одним числом, а целым интервалом. Разумеется, чемменьше длина этого интервала, тем точнее оценка параметра. Поэтому, если для оценки  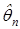некоторого параметра q справедливо неравенство 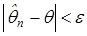, то число  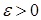характеризует точность оценки. Но статистические методы позволяют говорить только о том, что это неравенство выполняется с некоторой вероятностью.

Определение 24.Надёжностью (доверительной вероятностью) оценки 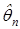 параметра q называется вероятность g того, что выполняется неравенство .

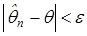Если заменить это неравенство двойным неравенством 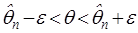, то получим, что надёжность определяется как

.

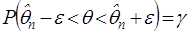(14)

Определение 25.Доверительным называется интервал, в который попадает неизвестный параметр с заданной надёжностью g.

Иными словами, доверительный интервал 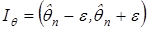 покрывает неизвестный параметр q с заданной надёжностью 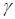. Выбор величины доверительной вероятности зависит от постановки задачи.Чаще всего берутся значения g=0,9;0,95;0,99;0,997.

 

Лекция 4

 

Критерий Колмогорова

 

Критерий Колмогорова является наиболее простым критерием проверки гипотезы о модели закона распределения. Он связывает эмпирическую функцию распределения 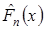 с функцией распределения  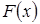непрерывной с.в. .

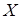Рассмотрим 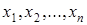– конкретную выборку из распределения с неизвестной функцией распределения 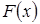. Пусть 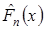–эмпирическая функция распределения. Сформулируем простую гипотезу 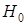: 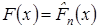, в качестве альтернативной выдвинем гипотезу : .

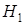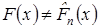Согласно критерию Колмогорова вводится в рассмотрение функция

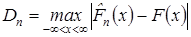
(29)

Эта функция называется статистикой Колмогорова и представляет собой максимальное отклонение эмпирической функции распределения 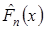 от гипотетической (теоретической) функции распределения .

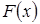Колмогоров доказал, что при 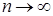 закон распределения с.в.  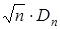стремится к закону распределенияКолмогорова независимо от вида распределения с.в. 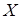, то есть

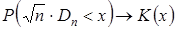
(30)

где 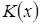– функция распределенияКолмогорова. Для нее составлена таблица значений, которой можно пользоваться при :

 

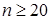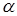
	0,1	0,05	0,02	0,01	0,001
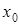
	1,224	1,358	1,520	1,627	1,950

 

Найдем такое значение 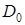, при котором выполняется равенство

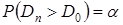
(31)

 

Рассмотрим уравнение 

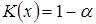
(32)

С помощью функции распределенияКолмогорова найдем корень 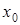 этого уравнения, тогда

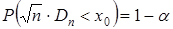
(33)

Следовательно, вероятность

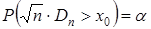
(34)

Таким образом,

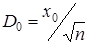
(35)

 Если 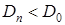, то гипотеза  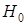принимается, в противном случае гипотеза  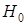отвергается.

 

 

Лекции по математической статистике

 

Лекция 1