Истечение жидкости из отверстия в дне сосуда происходит под действием силы гидростатического давления столба жидкости в сосуде. Рассмотрим сосуд, в дне которого имеется отверстие (рису-
нок 2.15).
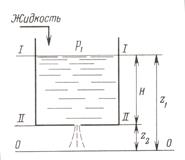 Рисунок 2.15 – К определению времени истечения жидкости из сосуда
Рисунок 2.15 – К определению времени истечения жидкости из сосуда
|
Пусть S – площадь сосуда, S0 – площадь отверстия. Жидкость в сосуде находится под атмосферным давлением, то есть Р1=Р2, S>>S0, тогда w 2 >> w 1. Рассмотрим два сечения I-I и II-II. Составим уравнение Бернулли для этих сечений:
| |
|
| (2.40) | |
где ζ – коэффициент сопротивления, учитывающий потерю напора в отверстии.
Тогда уравнение Бернулли будет выглядеть так:
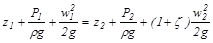 .
.
Из этого уравнения выразим скорость w2, причем скоростью w1 можно пренебречь.
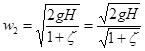
| (2.41) |
или
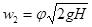 , ,
| (2.42) |
где φ = 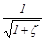 – коэффициент скорости истечения.
– коэффициент скорости истечения.
Тогда расход жидкости:
V = W 2 S сж = 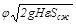 , ,
| (2.43) |
где ε = S сж / S 0 – коэффициент сжатия струи.
Таким образом, расход жидкости, вытекающей из отверстия в тонком дне сосуда, не зависит от формы сосуда.
Гидравлические методы измерения расхода
Жидкостей и газов
Гидравлический метод измерения расхода широко распространен в технике. Он основан на измерении перепада давления по сечению потока, возникающего при обтекании потоком местных сопротивлений. Приборы, в которых используется данный принцип, называют дроссельными. К ним относятся мерные диафрагмы, мерные сопла, труба Вентури. С помощью дроссельных приборов измеряют среднюю скорость потока.
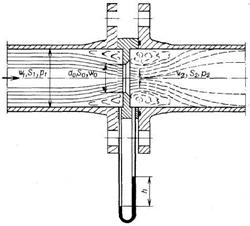
Мерная диафрагма изображена на рисунке 2.16.
Диафрагма 1 представляет собой тонкий диск с отверстием в центре, который устанавливают между фланцами с кольцевыми камерами 2. Разность давлений до и после диафрагмы замеряют с помощью дифференциального манометра 3. Он представляет собой U-образную трубку, заполненную жидкостью, которая не смешивается с рабочей и имеет большую плотность, чем рабочая жидкость.
|
Рисунок 2.16 – Диафрагма для измерения
расхода потока в трубопроводе
Уравнение для определения расхода жидкости:
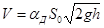 , ,
| (2.44а) |
где 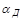 – коэффициент расхода диафрагмы,
– коэффициент расхода диафрагмы, 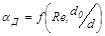 ;
;
S 0 – площадь сечения отверстия в диафрагме.
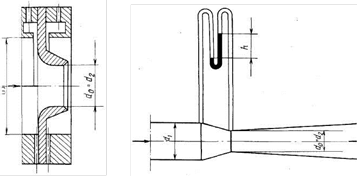
Мерное сопло (рисунок 2.17) представляет собой насадок с плавным закругленным входом и цилиндрическим выходом.
Гидравлическое сопротивление мерного сопла меньше, чем ди-афрагмы, но оно сложнее по устройству.
Труба Вентури (рисунок 2.18), представляющая собой насадок, по ходу потока сначала постепенно сужающийся, а затем постепенно расширяющийся до первоначального размера (диффузор). Благодаря плавному изменению сечения потока гидравлическое сопротивление трубы Вентури гораздо меньше, чем мерной диафрагмы и сопла, однако труба более громоздка. Из уравнения Бернулли следует, что с увеличением скорости движения давление должно уменьшаться, и, наоборот, с уменьшением скорости давление должно увеличиваться. Эта закономерность и используется в трубе Вентури. Зная диаметры D и d, по разности показаний пьезометров h, можно определить расход жидкости.
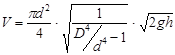 . .
| (2.44) |
|
| |
| Рисунок 2.17 – Мерное сопло | Рисунок 2.18 – Труба Вентури |
Для измерения скоростей по сечению потока может быть использована пневмометрическая трубка Пито–Прандтля (рисунок 2.19). Трубку вводят в поток так, чтобы изогнутый ее конец был направлен навстречу потоку. Тогда левая часть трубки замеряет сумму скоростного и статического напоров, а правая – только статический напор. Очевидно, что в данном случае дифференциальный манометр даст показания только о значении скоростного напора 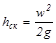 в данной точке. Тогда
в данной точке. Тогда
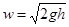 . .
| (2.45) |
Обычно замеряют осевую скорость (а если надо, то и эпюру скоростей по всему сечению потока). Для того чтобы определить среднюю скорость и расход потока, в выражение (2.44а) вводят поправочный коэффициент расхода 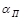 :
:
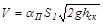
| (2.46) |
где S1 – сечение трубопровода;
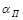 – коэффициент расхода пневмометрической трубки, определяемый по справочнику в зависимости от числа Рейнольдса.
– коэффициент расхода пневмометрической трубки, определяемый по справочнику в зависимости от числа Рейнольдса.
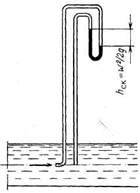
Рисунок 2.19 – Измерение локальной скорости жидкости
пневмометрической трубкой
Отметим, что коэффициенты расхода в уравнениях (2.44а) и (2.46) всегда меньше единицы.
Дата: 2019-02-02, просмотров: 391.
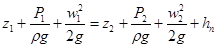 ,
, 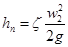 ,
,