2.1.1Плотность – количество массы жидкости, содержащееся в единице ее объема:
| r = m / V, кг/м3. | (2.1) |
Удельный вес – вес единицы объема жидкости:
| g = G / V = mg / V = r g, Н/м3. | (2.2) |
2.1.2Давление
Условия возникновения этого свойства: действие внешних сил, поверхностных и массовых. Рассмотрим (рисунок 2.1) некоторый объем покоящейся жидкости. Мысленно разделим этот объем на две части произвольной плоскостью АВ и отбросим верхнюю часть.
Для сохранения равновесия к нижней части плоскости необходимо приложить силы, которые заменят действие верхней части. Результирующую внешних поверхностных сил обозначим F. Если величину силы разделить на величину площадки S, то получим среднее значение давления на единицу площади Рср (или среднее гидростатическое давление):
| Рср = F / S . | (2.3) | |
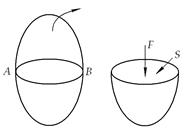 Рисунок 2.1 – К определению понятия гидростатического давления
Рисунок 2.1 – К определению понятия гидростатического давления
| Предел, к которому стремится среднее гидростатическое давление, когда величина площадки стремится к нулю, называется гидростатическим давлением в точке: Таким образом, гидростатическое давление - это напряжение, обусловленное действием рав-номерно распределенной поверхностной силы F на поверхность S. | |
Гидростатическое давление обладает следующими свойствами:
а) давление в любой точке жидкости, находящейся в равновесии, во всех направлениях одинаково;
б) давление всегда направлено по внутренней нормали к любой произвольно выбранной площадке жидкости, находящейся в покое;
в) гидростатическое давление в точке зависит от ее координат в пространстве, т.е. Р = f(x,y,z).
На этих свойствах давления основано действие многих практических устройств, например, гидравлического пресса.
Различают следующие виды давления: абсолютное, избыточное и вакуум.
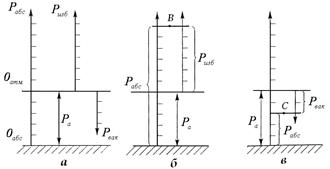 а – шкалы давления; б – взаимосвязь абсолютного и избыточного давлений; в – взаимосвязь абсолютного давления и давления вакуума
Рисунок 2.2 – Системы отсчета давления
а – шкалы давления; б – взаимосвязь абсолютного и избыточного давлений; в – взаимосвязь абсолютного давления и давления вакуума
Рисунок 2.2 – Системы отсчета давления
|
Взаимосвязь между всеми видами давления представлена ниже:
Pабс – абсолютное, Pабс = Pат + Pизб ;
Pизб – избыточное, Pизб = Pабс – Pат;
Pвак – вакуумное, Pизб = -Pвак .
2.2.3Вязкость
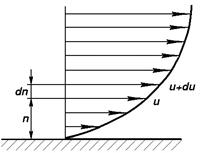
Вязкость – это способность жидкости сопротивляться сдвигу, т.е. свойство, обратное текучести (более вязкие жидкости являются менее текучими). Вязкость проявляется в возникновении касательных напряжений (напряжений трения). Рассмотрим слоистое течение жидкости вдоль стенки (рисунок 2.3).
а б
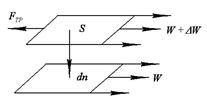
а – слои вдоль стенки; б – два слоя жидкости
Рисунок 2.3 – Схема течения жидкости вдоль стенки
В этом случае происходит торможение потока жидкости, обусловленное ее вязкостью. Причем скорость движения жидкости в слое тем ниже, чем ближе он расположен к стенке. Согласно гипотезе Ньютона касательное напряжение, возникающее в слое жидкости на расстоянии у от стенки, определяется зависимостью
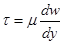 , ,
| (2.5) |
где dw / dy – градиент скорости (записан упрощенно), характеризующий интенсивность нарастания скорости w при удалении от стенки (по оси у).
Тогда сила сопротивления равна:
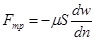 . .
| (2.6) |
Знак минус означает, что нормаль направлена в сторону уменьшения скорости.
Зависимости (2.5) и (2.6) называют законом трения Ньютона. Он был позднее экспериментально обоснован профессором Н.П. Петровым. Течения большинства жидкостей, используемых в гидравлических системах, подчиняются закону трения Ньютона, и их называют ньютоновскими жидкостями. Однако следует иметь в виду, что существуют жидкости, в которых закон (2.5) в той или иной степени нарушается. Такие жидкости называют неньютоновскими.
Величина 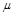 , входящая в (2.5) и (2.6), получила название ди-
, входящая в (2.5) и (2.6), получила название ди-
намической вязкости жидкости. Однако на практике более широкое применение нашла кинематическая вязкость:
| υ=μ/ρ, (м2/с). | (2.7) |
Вязкость жидкостей существенно зависит от температуры, причем вязкость капельных жидкостей с повышением температуры падает, а вязкость газов – растет. Это объясняется различным молекулярным строением жидкостей и газов.
Вязкость газов зависит от интенсивности хаотичного движения молекул. Происходит обмен молекулами, которые «тормозят» быстрый слой и ускоряют медленный. С ростом температуры эта интенсивность растет, и вязкость газов увеличивается. Вязкость жидкостей обусловлена силами межмолекулярного сцепления. Эти силы с ростом температуры ослабевают и вязкость падает.
2.2.4Поверхностное натяжение – работа, необходимая для создания единицы поверхности раздела фаз; сила, испытываемая молекулами, например, жидкости на границе газ–жидкость и направленная в глубину объема жидкости. Из-за него жидкость всегда принимает форму, соответствующую минимальной поверхности, в частности, капля имеет сферическую форму.
| s = F / S, | (2.8) |
где s – поверхностное натяжение, Дж/м2;
F – поверхностная энергия, Дж;
S – площадь поверхности, м2.
2.2.5Сжимаемость – это способность жидкости изменять свой объем под действием давления. Сжимаемость капельных жидкостей и газов существенно различается. Так, капельные жидкости при изменении давления изменяют свой объем крайне незначительно. Газы, наоборот, могут значительно сжиматься под действием давления и неограниченно расширяться при его отсутствии.
Сжимаемость капельных жидкостей характеризуется коэффициентом объемного сжатия b (Па-1):
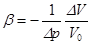 , ,
| (2.9) |
где Δр – изменение давления, Па;
D V – изменение объема под действием изменения давления, м3;
V 0 – начальный объем, м3.
Знак минус в формуле обусловлен тем, что при увеличении давления объем жидкости уменьшается, т.е. положительное приращение давления вызывает отрицательное приращение объема.
Величина, обратная коэффициенту объемного сжатия β, называется объемным модулем упругости жидкости (или модулем упругости).
Модуль упругости капельных жидкостей изменяется при изменении температуры и давления. Однако в большинстве случаев его считают постоянной величиной, принимая за нее среднее значение в данном диапазоне температур или давлений. Различают изотермический и адиабатический модули упругости. Причем обычно для расчетов используют изотермический модуль.
2.2.6Температурное расширение
Капельные жидкости изменяют свой объем и при колебании температуры. Это их свойство, называемое температурным расширением (так как с увеличением температуры объем их увеличивается), характеризуется коэффициентом объемного расширения β t, (К1):
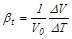 , ,
| (2.10) |
где ΔT – изменение температуры, К;
Δ V – изменение объема под действием изменения температуры, м3;
Vo – начальный объем, м3.
Газы весьма значительно изменяют свой объем при изменении температуры.
2.2.7Свойства жидкостей, обусловленные ее испарением
Упругость насыщенного пара – это свойство жидкости, которое возникает в том случае, если жидкость, имеющая свободную поверхность, длительное время находится в закрытом резервуаре. С истечением времени число молекул жидкости, переходящих в пар, может сравняться с числом молекул, возвратившихся в жидкость. Пар в этом случае становится насыщенным. Установившееся в нем давление называется давлением, или упругостью, насыщенного пара. Таким образом, упругость насыщенного пара – это установившееся при данной температуре давление пара, находящегося в равновесии с жидкостью.
Чем выше давление насыщенного пара при данной температуре, тем больше испаряемость жидкости. С увеличением температуры повышается упругость насыщенного пара. Если внешнее давление станет равным давлению насыщенного пара, жидкость закипит.
Кипение – это процесс парообразования внутри объема жидкости. Каждому значению температуры соответствует давление, при котором жидкость закипает. При низком давлении температура кипения жидкости низкая.
Для возникновения кипения необходимо, прежде всего, чтобы температура жидкости была выше температуры насыщения, а также необходимо наличие центров образования. Различают кипение на поверхности нагрева и кипение в объеме жидкости. Первый вид кипения обусловлен подводом теплоты к жидкости от соприкасающейся с ней поверхностью. Кипение в объеме жидкости обусловлено наличием значительного перегрева жидкости, возникающего, например, при внезапном снижении давления (ниже равновесного).
Кавитация – явление, возникающее в движущейся жидкости при понижении давления до упругости насыщенного пара и температуре окружающей среды. Кавитация сопровождается образованием парогазовых пузырьков, которые, перемещаясь с потоком жидкости в область с более высоким давлением, захлопываются, излучая при этом ударную волну. Захлопывание пузырьков вблизи границ течения может вызвать разрушение твердых поверхностей. Кавитация может возникнуть, например, при низких давлениях в трубопроводах.
Следует отметить, что кипение и кавитация нарушают сплошность жидкости и ограничивают область применения законов, основанных на представлении сплошной жидкой среды.
2.2.8Адгезия, когезия
Адгезия (GA) – работа, затрачиваемая на преодоление сил сцепления между разнородными молекулами, работа прилипания.
Когезия (Gk) – работа, затрачиваемая на преодоление сил сцепления между однородными молекулами.
Жидкость не имеет своей формы, то есть она всегда чем-то ограничена (другой жидкостью, газом или твердым телом). Если эта поверхность твердая, то жидкость может ее «смачивать» (рисунок 2.4а) или «не смачивать» (рисунок 2.4б).
 GA > Gk
а
GA > Gk
а
|
 Gk < GA
б
Gk < GA
б
|
| а) жидкость смачивает поверхность; Рисунок 2.4 – Соотношение между силами адгезии и когезии | |
Г идростатика
Гидростатика – наука о равновесии жидкости и практическом применении законов равновесия.
2.3.1 Основное уравнение гидростатики
Одним из выражений закона сохранения импульса является система уравнений Навье-Стокса (1.60). Уравнения Навье-Стокса совместно с уравнением неразрывности и сплошности потока (1.28), дополненные начальными и граничными условиями, служат для описания полей скоростей и давлений. В общем случае система уравнений Навье-Стокса не может быть решена аналитически. Решения этих уравнений получены лишь для достаточно упрощенных частных задач.
Так, в случае покоящейся жидкости (wx=wy=wz=0) уравнения Навье-Стокса переходят в дифференциальные уравнения равновесия Эйлера:
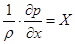 ; ; 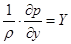 ; ; 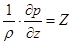
| (2.11) |
или
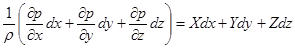 . .
| (2.12) |
Уравнение (2.12) можно записать в виде:
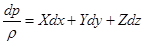 . .
| (2.13) |
Уравнение (2.13) является основным уравнением гидростатики.
Частные случаи основного уравнения гидростатики:
1) поверхности уровня (поверхности, давление во всех точках которых однаково, т.е dp =0):
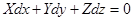 ; ;
| (2.14) |
2) из массовых сил действует только сила тяжести (X =0; Y =0; Z = - g):
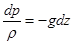
| (2.15) |
или, преобразовав, получим:
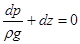 . .
| (2.16) |
В случае несжимаемой и однородной жидкости r=const. Тогда
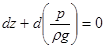 , ,
| (2.17) |
или
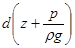 . .
| (2.17а) |
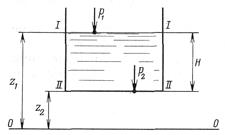 Рисунок 2.5 – К выводу закона Паскаля
Рисунок 2.5 – К выводу закона Паскаля
| Для двух произвольных горизонтальных плоскостей I - I и II - II (рисунок 2.5) уравнение (2.17а) примет вид:
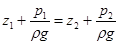 . (2.18)
Уравнение (2.18) часто называют основным уравнением гидростатики. Оно является частным случаем закона сохранения энергии. Переписав его от- . (2.18)
Уравнение (2.18) часто называют основным уравнением гидростатики. Оно является частным случаем закона сохранения энергии. Переписав его от-
|
носительно величины Р2, получим закон Паскаля:
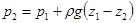 . .
| (2.19) |
Таким образом, внешнее давление, оказанное на свободную поверхность замкнутого объема несжимаемой жидкости, передается жидкостью одинаково всем ее точкам по всем направлениям.
Дата: 2019-02-02, просмотров: 329.
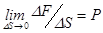 . (2.4)
. (2.4)