К основным уравнениям гидродинамики относятся:
а) уравнение неразрывности (сплошности) потока (см. уравнение (1.28))
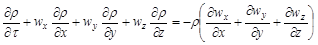 .
.
Из данного уравнения легко получить уравнение расхода. В случае однонаправленного (wy = wz = 0) установившегося движения ( 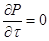 ) несжимаемой жидкости уравнение расхода в интегральной форме принимает вид: w ρS = const;
) несжимаемой жидкости уравнение расхода в интегральной форме принимает вид: w ρS = const;
б) уравнения Навье-Стокса (см. уравнение 1.60):
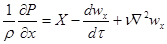 ;
;
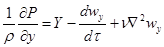 ;
;
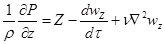 .
.
Система уравнений Навье-Стокса – один из важнейших законов сохранения количества движения. Его формулировка: Производная по времени от проекции количества движения системы на ось координат является суммой проекций на данную ось действующих на систему сил.
Частные случаи уравнения Навье-Стокса следующие.
1) Жидкость находится в относительном покое (wx = wy = wz = 0) – получим дифференциальные уравнения равновесия Эйлера
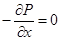 ; ; 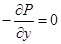 ; ; 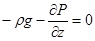 . .
| (2.24) |
Проинтегрируем уравнение (2.24) и получим основное уравнение гидростатики:
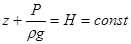 . .
| (2.25) |
2) Движение идеальной жидкости ( 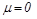 ):
):
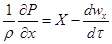 ; ; 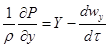 ; ; 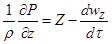 . .
| (2.26) |
Уравнения (2.26) являются дифференциальными уравнениями движения Эйлера.
При интегрировании уравнения (2.26) получаем уравнение Бернулли для идеальной жидкости:
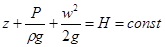 , ,
| (2.27) |
где z – нивелирная высота, или геометрический напор – это положе-ние данной частицы жидкости относительно произвольно выбранной горизонтальной плоскости сравнения. Энергетический смысл: удельная потенциальная энергия положения;
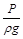 – статический, или пьезометрический, напор – давление столба жидкости над рассматриваемым уровнем. Энергетический смысл: удельная потенциальная энергия давления;
– статический, или пьезометрический, напор – давление столба жидкости над рассматриваемым уровнем. Энергетический смысл: удельная потенциальная энергия давления;
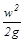 – скоростной, или динамический, напор. Энергетический смысл: удельная кинетическая энергия в данном сечении потока;
– скоростной, или динамический, напор. Энергетический смысл: удельная кинетическая энергия в данном сечении потока;
H – полный напор, или энергия жидкости, выраженная в метрах.
Для любого сечения или точки потока при установившемся движении идеальной жидкости сумма потенциальной ( 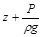 ) и кинетической (
) и кинетической ( 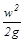 ) энергии жидкостей остается величиной постоянной. Таким образом, уравнение Бернулли выражает частный случай закона сохранения энергии.
) энергии жидкостей остается величиной постоянной. Таким образом, уравнение Бернулли выражает частный случай закона сохранения энергии.
Физический смысл уравнения Бернулли: в любом поперечном сечении потока идеальной жидкости полная удельная энергия жидкости постоянна и равна H.
Уравнение Бернулли для реальной жидкости выглядит иначе. Рассмотрим прямой участок трубопровода постоянного сечения (см. рисунок 2.13).
В случае идеальной жидкости E1 = E2, так как отсутствуют силы трения.
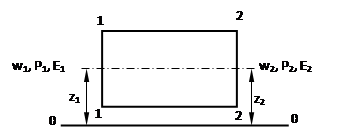 В случае реальной жидкости E1 > E2, так как частицы жидкости встречают сопротивление, вызванное силами вязкости и различными препятствиями.
В случае реальной жидкости E1 > E2, так как частицы жидкости встречают сопротивление, вызванное силами вязкости и различными препятствиями.
Рисунок 2.13 – К уравнению Бернулли для реальной жидкости
Таким образом, уравнение Бернулли для реальной жидкости:
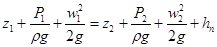 , ,
| (2.28) |
где 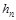 – величина гидравлического сопротивления или энергия, затрачиваемая на преодоление гидравлического сопротивления. Ее еще называют «потерянный напор».
– величина гидравлического сопротивления или энергия, затрачиваемая на преодоление гидравлического сопротивления. Ее еще называют «потерянный напор».
То есть энергия движущейся жидкости расходуется на преодоление сопротивлений и превращается в тепло. Это тепло идет на нагревание потока и рассеивается в окружающую среду. Поэтому во всяком последующем положении или сечении потока энергия частицы будет меньше, чем в предыдущем.
Для жидкости, текущей по горизонтальному трубопроводу постоянного сечения с постоянной скоростью, потерянный напор рассчитывается по формуле:
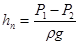 . .
| (2.29) |
С помощью уравнения Бернулли можно определить необходимый напор (или давление) для того, чтобы жидкость с заданной скоростью транспортировалась по данному каналу (трубопроводу), а также скорость и расход жидкости, время истечения жидкости из отверстия в резервуаре.
2.4.3 Гидравлическое сопротивление трубопроводов
и аппаратов
Для определения движущей силы гидродинамических процесссов необходимо знать потерянный напор hn (2.29), который складывается из потерь напора на трение h тр и на преодоление так называемых местных сопротивлений h мс:
| hn = h тр + h мс. | (2.30) |
Причиной потерь на трение является вязкость жидкости. Потери на трение рассчитывают по формуле:
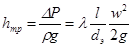 , ,
| (2.31) |
где l – длина трубопровода, м;
d э – эквивалентный диаметр трубопровода, м;
w – средняя скорость, м;
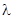 – коэффициент потерь на трение.
– коэффициент потерь на трение.
Коэффициент потерь на трение зависит от числа Рейнольдса и шероховатости трубы.
При ламинарном режиме
ΔР ~w и 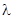 =64/Re. =64/Re.
| (2.32) |
При турбулентном режиме выделяют три области:
1) область гидравлически гладких труб 2300<Re<10/ε (где ε – относительная шероховатость)
ΔР ~w 1,75 и 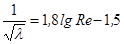 ; ;
| (2.33) |
2) область смешанного трения 10/ ε <Re<560/ε
ΔР ~ w1,75 ÷ 2 и 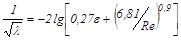 ; ;
| (2.34) |
3) автомодельная область или область квадратичного сопротивления Re>560/ε
ΔР ~ w2 и 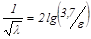 . .
| (2.35) |
Коэффициент сопротивления трения 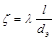 , тогда величина потерь на трение будет равна:
, тогда величина потерь на трение будет равна:
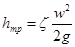 . .
| (2.36) |
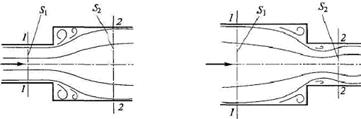
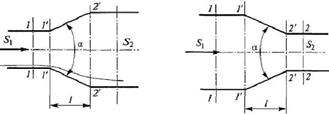
Потери напора на преодоление местных сопротивлений возникают при движении жидкости через сужения и расширения в трубопроводах, через краны, задвижки и другие местные сопротивления. Местные сопротивления – это такие вставки трубопровода, которые изменяют поток по направлению, по величине, по величине и направлению одновременно (рисунок 2.14).
Потери напора на преодоление местных сопротивлений h мс, также как и h тр , выражаются через скоростной напор 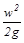 :
:
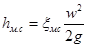 , ,
| (2.37) |
где 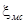 - коэффициент местного сопротивления.
- коэффициент местного сопротивления.
Коэффициент местного сопротивления зависит от числа Рейнольдса и вида сопротивления и является справочной величиной.
Общий потерянный напор можно рассчитать как сумму потерь на трение и на преодоление местных сопротивлений:
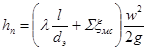 . .
| (2.38) |
 а б
а б
 в г
в г
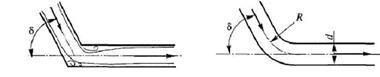 д е
а – внезапное расширение; б – внезапное сужение; в – плавное
расширение; г – плавное сужение; д – поворот трубы без
закругления; е – поворот трубы с закруглением
Рисунок 2.14 – Местные сопротивления
д е
а – внезапное расширение; б – внезапное сужение; в – плавное
расширение; г – плавное сужение; д – поворот трубы без
закругления; е – поворот трубы с закруглением
Рисунок 2.14 – Местные сопротивления
|
Потеря давления:
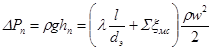 . .
| (2.39) |
1
1
Дата: 2019-02-02, просмотров: 340.