МОДУЛЬ 2 : Основы гидравлики
Гидравлика – прикладная наука о законах равновесия и движения жидкостей и о способах применения этих законов к решению конкретных технических задач.
Практическое значение гидравлики весьма велико, так как она является основой ряда специальных дисциплин. Раздел гидравлики, в котором рассматриваются законы равновесия жидкостей, называют гидростатикой; часть гидравлики, где изучаются законы движения жидкости, называется гидродинамикой. Эти же задачи рассматриваются в теоретической гидромеханике. Однако методы исследования при этом различны. В гидравлике применяются упрощенные приемы решения задач, а в теоретической гидромеханике используются строгие математические методы, позволяющие получить общие теоретические решения задач.
Практическое применение законов гидростатики позволяет решать следующие задачи: определять давление в любой точке жидкости, вести расчет сосудов под давлением, понимать действие гидравлических устройств (гидравлических прессов) и т.д.
Практическое применение законов гидродинамики позволит рассчитать энергию на перемещение жидкости, диаметр трубопроводов и аппаратов, а также процесс истечения жидкости из отверстия и через насадки.
Гидравлические машины предназначены для преобразования механической энергии двигателя в энергию перемещаемой жидкости (насосы) или гидравлической энергии потока жидкости в механическую энергию (гидродвигатели).
Итак, предметом изучения в предлагаемом курсе является жидкость, а также механические устройства, в которых осуществляется энергообмен между их подвижными элементами и жидкостью.
2.1 О сновные понятия и определения гидравлики
2.1.1Жидкость – физическое тело, обладающее большой подвижностью частиц, которая объясняется слабой связью между молекулами. Поэтому жидкости легко изменяют свою форму, т.е. легко деформируются, не дробясь на части, под действием сил самой незначительной величины или, другими словами, обладают текучестью при приложении к ним незначительных сил сдвига. Жидкость не имеет своей формы, но принимает форму сосуда, в котором она находится.
Все жидкости делятся на капельные и газообразные. Таким образом, под это определение попадают и газы, которые, в отличие от жидкостей в общепринятом смысле этого слова (или капельных жидкостей), называются «упругими» жидкостями.
Капельная жидкость имеет объем, и если объем меньше объема сосуда, то жидкость занимает часть объема сосуда и образует свободную поверхность. В отличие от капельных жидкостей газы, как упругие жидкости, не имеют своих определенных формы и объема. Они всегда занимают весь объем сосуда, в котором находятся.
Жидкости отличаются от твердых тел тем, что они обладают такими свойствами, как адгезия, удельный вес, поверхностное натяжение и упругость насыщенного пара.
2.1.2Идеальная жидкость – жидкость, которая не сжимается под действием давления, не изменяет плотности при изменении температуры и не обладает вязкостью.
2.1.3Сплошная среда – жидкость без пустот, разрывов и трещин, диаметр частиц больше длины свободного пробега молекул 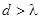 . Модель сплошной среды позволяет применять для анализа такой мощный математический аппарат, как дифференциальное и интегральное исчисление.
. Модель сплошной среды позволяет применять для анализа такой мощный математический аппарат, как дифференциальное и интегральное исчисление.
Во всех последующих расчетах предполагается, что жидкость – сплошная среда.
Г идростатика
Гидростатика – наука о равновесии жидкости и практическом применении законов равновесия.
2.3.1 Основное уравнение гидростатики
Одним из выражений закона сохранения импульса является система уравнений Навье-Стокса (1.60). Уравнения Навье-Стокса совместно с уравнением неразрывности и сплошности потока (1.28), дополненные начальными и граничными условиями, служат для описания полей скоростей и давлений. В общем случае система уравнений Навье-Стокса не может быть решена аналитически. Решения этих уравнений получены лишь для достаточно упрощенных частных задач.
Так, в случае покоящейся жидкости (wx=wy=wz=0) уравнения Навье-Стокса переходят в дифференциальные уравнения равновесия Эйлера:
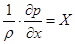 ; ; 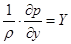 ; ; 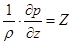
| (2.11) |
или
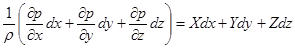 . .
| (2.12) |
Уравнение (2.12) можно записать в виде:
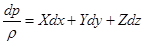 . .
| (2.13) |
Уравнение (2.13) является основным уравнением гидростатики.
Частные случаи основного уравнения гидростатики:
1) поверхности уровня (поверхности, давление во всех точках которых однаково, т.е dp =0):
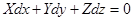 ; ;
| (2.14) |
2) из массовых сил действует только сила тяжести (X =0; Y =0; Z = - g):
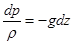
| (2.15) |
или, преобразовав, получим:
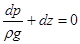 . .
| (2.16) |
В случае несжимаемой и однородной жидкости r=const. Тогда
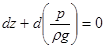 , ,
| (2.17) |
или
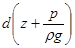 . .
| (2.17а) |
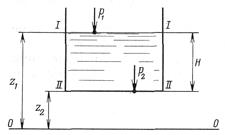 Рисунок 2.5 – К выводу закона Паскаля
Рисунок 2.5 – К выводу закона Паскаля
| Для двух произвольных горизонтальных плоскостей I - I и II - II (рисунок 2.5) уравнение (2.17а) примет вид:
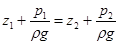 . (2.18)
Уравнение (2.18) часто называют основным уравнением гидростатики. Оно является частным случаем закона сохранения энергии. Переписав его от- . (2.18)
Уравнение (2.18) часто называют основным уравнением гидростатики. Оно является частным случаем закона сохранения энергии. Переписав его от-
|
носительно величины Р2, получим закон Паскаля:
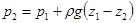 . .
| (2.19) |
Таким образом, внешнее давление, оказанное на свободную поверхность замкнутого объема несжимаемой жидкости, передается жидкостью одинаково всем ее точкам по всем направлениям.
Гидравлический пресс
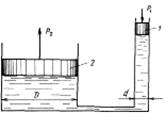 Рисунок 2.6 – Схема
гидравлического пресса
Рисунок 2.6 – Схема
гидравлического пресса
| В основу работы гидравлического пресса положен закон Паскаля. Сила давления на поршень 1 и на поршень 2 соответственно составит: р 1 = р S1 = p p d2/4, Р 2 = pS2 =p p D2/4, отсюда P 2 = P 1 D 2 / d 2 . |
Поршень 2 передаст силу давления, во столько раз превышающую силу, приложенную к поршню 1, во сколько раз поперечное сечение цилиндра 2 больше, чем сечение цилиндра 1.
Гидравлические прессы применяются для прессования и брикетирования пластических масс, металлокерамических порошков и др.
Г идродинамика
Гидродинамика – наука, изучающая законы движения жидкостей и практическое их применение.
Режимы движения жидкостей
Чтобы правильно решить одну из основных задач практики гидравлики, т.е. определить величину гидравлических сопротивлений, необходимо составить ясное представление о механизме самого движения жидкости. При исследовании этого вопроса пришли к заключению о существовании двух различных режимов движения: ламинарного и турбулентного.
Ламинарный поток характеризуется тем, что каждая частица движется с постоянной скоростью параллельно оси потока (рису-
нок 2.10а), т.е. все частицы жидкости движутся в продольном направлении. Но это не означает, что в потоке полностью отсутствуют возмущения. В этом потоке инерционные силы, возникающие при возмущениях, малы по сравнению с силами вязкости. Мерой отношения этих двух родов сил является критерий Рейнольдса. Большие силы вязкости гасят возмущения. Однако по мере роста скорости силы инерции все больше превышают силы вязкости, критерий Рейнольдса растет.
Наконец, при каком-то критическом значении критерия Рейнольдса (в круглой трубе оно равно приблизительно 2300) вязкость уже не может гасить все возмущения. Вследствие случайных причин какая-то частица жидкости может «сойти со своего места» в потоке. При этом из-за неразрывности потока она будет «расталкивать» другие частицы, передавая им возмущение.
При дальнейшем росте критерия Рейнольдса ламинарное течение оказывается практически невозможным. Наличие хаотических пульсаций скорости, направленных в различные стороны, и определяет турбулентное течение.
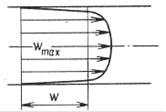
В турбулентном потоке перенос количества движения в поперечном направлении происходит иначе, чем в ламинарном. Представим себе, что частица жидкости, движущаяся у оси потока и поэтому имеющая максимальную скорость, за счет турбулентной пульсации переместилась ближе к стенке. Не трудно понять, что при этом она перенесет с собой в эту периферийную часть потока большую скорость (точнее большее количество движения), которой она обладала. Навстречу же ей перемещаются частицы, обладающие малыми поступательными скоростями, что снижает среднюю скорость у оси. Таким образом, из-за турбулентных пульсаций происходит перемешивание «быстрых» (движущихся у оси) и «медленных» (периферийных) частиц, выравнивающее средние скорости в сечении (рисунок 2.10б).
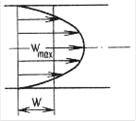
| 
|
| а) | б) |
| Рисунок 2.10 – Профили скоростей в ламинарном (а) | |
Совершенно таким же образом турбулентное перемешивание выравнивает по поперечному сечению температуру и концентрации. Аналогично вышесказанному в таких случаях говорят о турбулентной диффузии и турбулентной теплопроводности. Это конвективные аналоги истинных (молекулярных) диффузии и теплопроводности. Однако картина распределения скоростей, температур и концентраций по поперечному сечению еще не полна. Частицы, подверженные турбулентным пульсациям скорости, дойти до стенки не могут, так как по мере приближения к ней турбулентные пульсации скорости затухают. В результате около стенки образуется тонкий слой, в котором конвективный перенос становится исчезающе малым, – это пограничный слой. Перенос осуществляется здесь в основном за счет молекулярных механизмов, непосредственно у твердой стенки скорость жидкости равна нулю.
Турбулентный режим движения в технологических аппаратах наиболее часто встречается не ламинарный, а турбулентный режим движения. В турбулентном потоке отдельно взятая частица жидкости движется по сложной криволинейной траектории. Поэтому скорость ее движения в данной точке в данный момент времени называют мгновенной скоростью. Любую мгновенную скорость можно разложить на составляющие (рисунок 2.11).
Графические изменения этих составляющих в зависимости от времени называют графиками пульсаций.
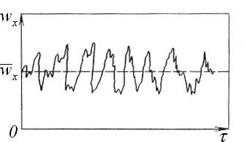
Рисунок 2.11 – Истинная wx и осредненная 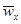
локальные скорости жидкости в турбулентном потоке
Поскольку мгновенная скорость 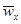 в данной точке не постоянна, а изменяется во времени, в гидродинамике для удобства исследования потока вводится понятие усредненной скорости, то есть средней скорости в данной точке за достаточно большой промежуток времени:
в данной точке не постоянна, а изменяется во времени, в гидродинамике для удобства исследования потока вводится понятие усредненной скорости, то есть средней скорости в данной точке за достаточно большой промежуток времени:
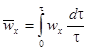 . .
| (2.23) |
Усредненную скорость иногда называют средней местной скоростью.
Разность между истинным (w) и усредненным ( 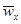 ) значениями мгновенной местной скорости называется пульсационной скоростью (wx). Понятие усредненной скорости нельзя смешивать с понятием средней скорости, представляющей собой не среднюю по времени скорость в данной точке, а среднюю скорость для всего поперечного сечения.
) значениями мгновенной местной скорости называется пульсационной скоростью (wx). Понятие усредненной скорости нельзя смешивать с понятием средней скорости, представляющей собой не среднюю по времени скорость в данной точке, а среднюю скорость для всего поперечного сечения.
В турбулентном потоке всегда наблюдается пульсация скоростей, вследствие чего между соседними слоями жидкости возникает обмен частицами, вызывающий непрерывное перемешивание жидкости. На рисунке 2.12 представлена схематизированная модель турбулентного потока.
По этой схеме у стенок образуется весьма тонкий слой, в котором скорость изменяется не скачкообразно, а непрерывно, и движение жидкости происходит по законам ламинарного режима.
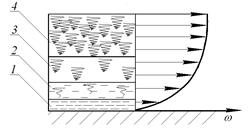
1 – вязкий подслой; 2 – переходный (буферный) слой;
3 – полностью турбулентный слой; 4 – турбулентное ядро потока
Рисунок 2.12 – Модель структуры поперечного сечения
турбулентного потока
Основная часть потока (ядро), связанная с этим слоем, называемым вязким (или ламинарным) подслоем, короткой переходной зоной, движется турбулентно с почти одинаковой для всех частиц жидкости осредненной скоростью. Толщина этого подслоя обычно определяется долями миллиметра и зависит от величины Re. Однако, несмотря на малую толщину, вязкий подслой оказывает решающее влияние на интенсивность тепло- и массопереноса.
Жидкостей и газов
Гидравлический метод измерения расхода широко распространен в технике. Он основан на измерении перепада давления по сечению потока, возникающего при обтекании потоком местных сопротивлений. Приборы, в которых используется данный принцип, называют дроссельными. К ним относятся мерные диафрагмы, мерные сопла, труба Вентури. С помощью дроссельных приборов измеряют среднюю скорость потока.
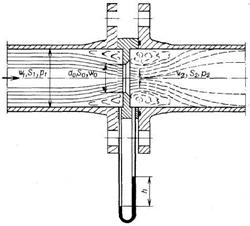
Мерная диафрагма изображена на рисунке 2.16.
Диафрагма 1 представляет собой тонкий диск с отверстием в центре, который устанавливают между фланцами с кольцевыми камерами 2. Разность давлений до и после диафрагмы замеряют с помощью дифференциального манометра 3. Он представляет собой U-образную трубку, заполненную жидкостью, которая не смешивается с рабочей и имеет большую плотность, чем рабочая жидкость.
|
Рисунок 2.16 – Диафрагма для измерения
расхода потока в трубопроводе
Уравнение для определения расхода жидкости:
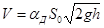 , ,
| (2.44а) |
где 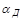 – коэффициент расхода диафрагмы,
– коэффициент расхода диафрагмы, 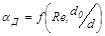 ;
;
S 0 – площадь сечения отверстия в диафрагме.
Мерное сопло (рисунок 2.17) представляет собой насадок с плавным закругленным входом и цилиндрическим выходом.
Гидравлическое сопротивление мерного сопла меньше, чем ди-афрагмы, но оно сложнее по устройству.
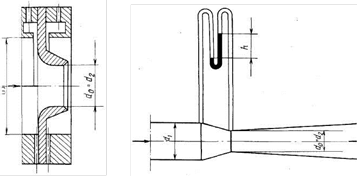
Труба Вентури (рисунок 2.18), представляющая собой насадок, по ходу потока сначала постепенно сужающийся, а затем постепенно расширяющийся до первоначального размера (диффузор). Благодаря плавному изменению сечения потока гидравлическое сопротивление трубы Вентури гораздо меньше, чем мерной диафрагмы и сопла, однако труба более громоздка. Из уравнения Бернулли следует, что с увеличением скорости движения давление должно уменьшаться, и, наоборот, с уменьшением скорости давление должно увеличиваться. Эта закономерность и используется в трубе Вентури. Зная диаметры D и d, по разности показаний пьезометров h, можно определить расход жидкости.
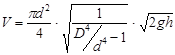 . .
| (2.44) |
|
| |
| Рисунок 2.17 – Мерное сопло | Рисунок 2.18 – Труба Вентури |
Для измерения скоростей по сечению потока может быть использована пневмометрическая трубка Пито–Прандтля (рисунок 2.19). Трубку вводят в поток так, чтобы изогнутый ее конец был направлен навстречу потоку. Тогда левая часть трубки замеряет сумму скоростного и статического напоров, а правая – только статический напор. Очевидно, что в данном случае дифференциальный манометр даст показания только о значении скоростного напора 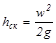 в данной точке. Тогда
в данной точке. Тогда
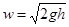 . .
| (2.45) |
Обычно замеряют осевую скорость (а если надо, то и эпюру скоростей по всему сечению потока). Для того чтобы определить среднюю скорость и расход потока, в выражение (2.44а) вводят поправочный коэффициент расхода 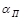 :
:
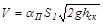
| (2.46) |
где S1 – сечение трубопровода;
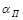 – коэффициент расхода пневмометрической трубки, определяемый по справочнику в зависимости от числа Рейнольдса.
– коэффициент расхода пневмометрической трубки, определяемый по справочнику в зависимости от числа Рейнольдса.
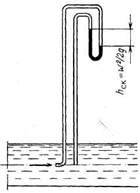
Рисунок 2.19 – Измерение локальной скорости жидкости
пневмометрической трубкой
Отметим, что коэффициенты расхода в уравнениях (2.44а) и (2.46) всегда меньше единицы.
Транспортирование жидкостей
Применяемые в химической технологии жидкости и газы часто необходимо транспортировать по трубопроводам. Транспортирование жидкости с более низкого уровня на более высокий осуществляется с помощью гидравлических машин – насосов, в которых механическая энергия двигателя преобразуется в энергию транспортируемой жидкости вследствие повышения ее давления.
Классификация насосов
По принципу действия насосы подразделяют на объемные и динамические.
В объемных насосах энергия и давление повышаются в результате вытеснения жидкости из замкнутого пространства телами, движущимися возвратно-поступательно или вращательно. В соответствии с этим по форме движения рабочих органов их подразделяют на возвратно-поступательные (поршневые, плунжерные, диафрагменные) и вращательные, или роторные (шестеренные, винтовые и др.).
В динамических насосах энергия и давление жидкости повышаются под действием центробежной силы, возникающей при вращении лопастных колес (например, в центробежных и осевых насосах), или сил трения (например, в струйных и вихревых насосах). Поэтому по виду силового действия на жидкость динамические насосы подразделяют на лопастные и насосы трения.
Наиболее распространенными динамическими насосами являются лопастные. К данному виду насосов относятся центробежные и осевые. Работа этих насосов основана на общем принципе силового взаимодействия лопастей рабочего колеса с обтекающим их потоком перекачиваемой жидкости. Однако механизм этого взаимодействия у центробежных и осевых насосов различен, что, естественно, приводит к существенным различиям в их конструкциях и эксплуатационных показателях.
Основные параметры насосов
К основным параметрам насосов относят производительность, напор, мощность.
Производительность Q насоса – объем жидкости, подаваемый насосом в нагнетательный трубопровод в единицу времени (м3/с).
Напор Н (м) представляет собой избыточную удельную энергию, сообщаемую насосом единице массы жидкости.
Полезная мощность насоса N П , затрачиваемая на сообщение жидкости энергии, равна произведению удельной энергии на массовый расход жидкости:
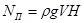 . .
| (2.52) |
Действительная мощность на валу насоса N Д – мощность, потребляемая насосом; больше полезной мощности вследствие потерь в самом насосе.
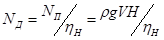 . .
| (2.53) |
Наиболее распространенным типом объемных насосов являются поршневые. Насос состоит из цилиндра 1 (рисунок 2.22), в котором с помощью кривошипно-шатунного механизма движется возвратно-поступательно поршень 2.
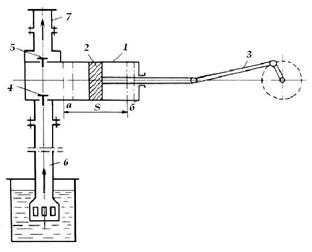
1 – цилиндр; 2 – поршень; 3 – кривошипно-шатунный механизм;
4 и 5 – соответственно всасывающий и нагнетательный клапаны;
6 и 7 – соответственно всасывающий и нагнетательный трубопроводы
Рисунок 2.22 – Горизонтальный поршневой насос простого действия
При движении поршня слева направо (из крайнего левого положения а) в цилиндре возникает разрежение, вследствие чего всасывающий клапан 4 поднимается, и жидкость из резервуара по всасывающему трубопроводу 6 поступает в цилиндр 1 и движется за поршнем. Нагнетательный клапан 5 при этом закрыт, так как на него действует сила давления жидкости, находящейся в нагнетательном трубопроводе 7. При ходе поршня справа налево (из крайнего правого положения б) в цилиндре создается избыточное давление, под действием которого закрывается (опускается) всасывающий клапан, а нагнетательный клапан 5 открывается, и жидкость поступает в нагнетательный трубопровод. Таким образом, в рассмотренном насосе за один оборот вала кривошипно-шатунного механизма (при этом поршень делает два хода – слева направо и справа налево) происходит одно всасывание и одно нагнетание, т.е. процесс перекачивания жидкости таким насосом, который называют насосом простого действия, осуществляется неравномерно.
В зависимости от числа всасываний и нагнетаний за один оборот вала кривошипно-шатунного механизма или за два хода S поршня (см. рисунок 2.22) поршневые насосы подразделяют на насосы простого и многократного действия. У последних достигается более равномерная подача и более высокая производительность, чем у насосов простого действия.
По расположению поршня различают горизонтальные и вертикальные поршневые насосы. В горизонтальных насосах вследствие неравномерного давления поршня на цилиндр происходит более быстрый, чем в вертикальных насосах, выход из строя. При работе в условиях высокого давления поршневые насосы требуют сложных уплотняющих устройств.
Производительность поршневого насоса простого действия определяется следующим образом:
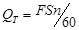 , ,
| (2.54) |
где F – площадь сечения поршня, м2;
S – длина хода поршня; м;
n – число оборотов кривошипно-шатунного механизма, об/мин.
Действительная производительность насоса будет меньше теоретической вследствие утечки жидкости через неплотности в сальниках, клапанах и запаздывания открытия и закрытия клапана. Кроме того, во всасываемой жидкости вследствие разрежения могут выделяться пузырьки растворенного в ней воздуха с образованием в цилиндре воздушных «мешков», снижающих подачу насоса. Все эти потери учитываются объемным КПД, или коэффициентом подачи η V.
Поэтому действительная производительность Q Д насоса простого действия определяется по формуле
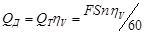 , ,
| (2.55) |
где h v – объемный КПД или коэффициент подачи.
Основными достоинствами поршневых и плунжерных насосов являются высокий КПД и возможность подачи незначительных объемов жидкостей, в том числе высоковязких, под любым заданным давлением. Однако неравномерность подачи, наличие легко изнашиваемых клапанов, сложность соединений с двигателем, тихоходность, а следовательно, большие размеры и масса существенно ограничивают области применения поршневых и плунжерных насосов в химической промышленности.
Наиболее распространенными динамическими насосами являются центробежные. Основным рабочим органом центробежного насоса (рисунок 2.23) является свободно вращающееся внутри спиралевидного (или улиткообразного) корпуса 1 колесо 2, насаженное на вал 9.
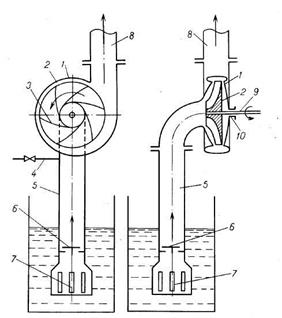
1 – корпус; 2 – рабочее колесо; 3 – лопатки; 4 – линия для залива
насоса перед пуском; 5 – всасывающий трубопровод; 6 – обратный
клапан; 7 – фильтр; 8 – нагнетательный трубопровод; 9 – вал; 10 – сальник
Рисунок 2.23 – Центробежный насос
Между дисками колеса, соединяя их в единую конструкцию, находятся лопасти (лопатки) 3, плавно изогнутые в сторону, противоположную направлению вращения колеса.
Внутренние поверхности дисков и поверхности лопаток образуют так называемые межлопастные каналы колеса, которые при работе насоса заполнены перекачиваемой жидкостью. Всасывание и нагнетание жидкости в центробежных насосах происходит равномерно и непрерывно под действием центробежной силы, возникающей при вращении колеса.
При переходе жидкости из канала рабочего колеса 2 в корпус 1 происходит резкое снижение скорости, в результате чего кинетическая энергия жидкости превращается в потенциальную энергию давления, необходимую для подачи жидкости на заданную высоту. При этом в центре колеса создается разрежение, и вследствие этого жидкость непрерывно поступает по всасывающему трубопроводу в корпус насоса, а затем в межлопастные каналы рабочего колеса. Если перед пуском центробежного насоса всасывающий трубопровод 5 и корпус 1 не залиты жидкостью, то разрежения, возникающего в этом случае при вращении колеса, будет недостаточно для подъема жидкости в насос (вследствие зазоров между колесом и корпусом). Поэтому перед пуском центробежного насоса его необходимо залить жидкостью с помощью линии 4. Для того, чтобы жидкость при этом не выливалась из насоса, на всасывающем трубопроводе устанавливают обратный клапан 6. Герметизация нacoca осуществляется с помощью сальника 10.
Для отвода жидкости в корпусе насоса имеется расширяющаяся спиралевидная камера; жидкость из рабочего колеса поступает сначала в эту камеру, а затем в нагнетательный трубопровод 8.
Центробежные насосы обеспечивают плавную и непрерывную подачу перекачиваемой жидкости при достаточно высоких значениях коэффициента полезного действия. Относительно простое устройство обеспечивает их высокую надежность и достаточную долговечность. Отсутствие поверхностей трения, клапанов создает возможности для перекачивания загрязненных жидкостей. Простота непосредственного соединения с высокооборотными двигателями способствует компактности насосной установки и повышению ее КПД. Все эти достоинства лопастных насосов, прежде всего центробежных, привели к тому, что они являются основными насосами в химической промышленности. К недостаткам центробежных насосов относится ограниченность применения в области малых производительностей и большие напоров, что объясняется снижением КПД при увеличении числа ступеней для достижения высоких значений Н.
Вопросы для самоконтроля
1. Что понимают под гидравликой? Гидростатика и гидродинамика, их основные задачи.
2. Сформулируйте основные понятия и определения гидравлики.
3. Перечислите основные свойства жидкостей.
4. Что представляет собой гидростатическое давление? Какими свойствами оно обладает?
5. Чем обусловлено торможение движения жидкости у твердой поверхности (например, у поверхности движущейся пластины или у стенок канала)?
6. Раскройте понятия динамической и кинематической вязкости жидкости.
7. Выведите основное уравнение гидростатики. Укажите области его применения.
8. Что такое средняя скорость движения жидкости? Назовите виды и режимы движения.
9. Сформулируйте основные различия ламинарного и турбулентного течения. Изобразите эпюры скоростей для этих режимов движения. Назовите области турбулентного потока.
10. Напишите уравнение Бернулли для потока идеальной жидкости в горизонтальных трубах.
11. Раскройте физический смысл уравнения Бернулли.
12. Как рассчитывают потери напора на трение и местные сопротивления в трубопроводах и аппаратах?
13. Как влияет шероховатость на гидравлическое сопротивление при движении жидкости в ламинарном и турбулентном режимах?
14. В чем состоит принцип гидравлических методов измерения расходов жидкостей и газов?
15. Как выбрать оптимальный диаметр трубопровода или канала?
16. Как определить расход энергии на перемещение жидкости?
17. Приведите классификацию насосов.
18. Как рассчитать мощность на валу насоса?
19. Опишите принцип действия поршневого насоса.
20. Каковы достоинства и недостатки у центробежных насосов?
1
МОДУЛЬ 2 : Основы гидравлики
Гидравлика – прикладная наука о законах равновесия и движения жидкостей и о способах применения этих законов к решению конкретных технических задач.
Практическое значение гидравлики весьма велико, так как она является основой ряда специальных дисциплин. Раздел гидравлики, в котором рассматриваются законы равновесия жидкостей, называют гидростатикой; часть гидравлики, где изучаются законы движения жидкости, называется гидродинамикой. Эти же задачи рассматриваются в теоретической гидромеханике. Однако методы исследования при этом различны. В гидравлике применяются упрощенные приемы решения задач, а в теоретической гидромеханике используются строгие математические методы, позволяющие получить общие теоретические решения задач.
Практическое применение законов гидростатики позволяет решать следующие задачи: определять давление в любой точке жидкости, вести расчет сосудов под давлением, понимать действие гидравлических устройств (гидравлических прессов) и т.д.
Практическое применение законов гидродинамики позволит рассчитать энергию на перемещение жидкости, диаметр трубопроводов и аппаратов, а также процесс истечения жидкости из отверстия и через насадки.
Гидравлические машины предназначены для преобразования механической энергии двигателя в энергию перемещаемой жидкости (насосы) или гидравлической энергии потока жидкости в механическую энергию (гидродвигатели).
Итак, предметом изучения в предлагаемом курсе является жидкость, а также механические устройства, в которых осуществляется энергообмен между их подвижными элементами и жидкостью.
2.1 О сновные понятия и определения гидравлики
2.1.1Жидкость – физическое тело, обладающее большой подвижностью частиц, которая объясняется слабой связью между молекулами. Поэтому жидкости легко изменяют свою форму, т.е. легко деформируются, не дробясь на части, под действием сил самой незначительной величины или, другими словами, обладают текучестью при приложении к ним незначительных сил сдвига. Жидкость не имеет своей формы, но принимает форму сосуда, в котором она находится.
Все жидкости делятся на капельные и газообразные. Таким образом, под это определение попадают и газы, которые, в отличие от жидкостей в общепринятом смысле этого слова (или капельных жидкостей), называются «упругими» жидкостями.
Капельная жидкость имеет объем, и если объем меньше объема сосуда, то жидкость занимает часть объема сосуда и образует свободную поверхность. В отличие от капельных жидкостей газы, как упругие жидкости, не имеют своих определенных формы и объема. Они всегда занимают весь объем сосуда, в котором находятся.
Жидкости отличаются от твердых тел тем, что они обладают такими свойствами, как адгезия, удельный вес, поверхностное натяжение и упругость насыщенного пара.
2.1.2Идеальная жидкость – жидкость, которая не сжимается под действием давления, не изменяет плотности при изменении температуры и не обладает вязкостью.
2.1.3Сплошная среда – жидкость без пустот, разрывов и трещин, диаметр частиц больше длины свободного пробега молекул 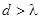 . Модель сплошной среды позволяет применять для анализа такой мощный математический аппарат, как дифференциальное и интегральное исчисление.
. Модель сплошной среды позволяет применять для анализа такой мощный математический аппарат, как дифференциальное и интегральное исчисление.
Во всех последующих расчетах предполагается, что жидкость – сплошная среда.
Дата: 2019-02-02, просмотров: 414.