Пример. Интенсивность равномерного спроса составляет 2000 единиц товара в год, организационные издержки для одной партии составляют 50 у.е., цена единицы товара составляет 100 у.е., издержки содержания запаса равны 1 у.е. за единицу товара в год, т. е. d = 2000 ед.товара в год, s = 50 у.е., с = 100 у.е.,
h = 1 у.е./ед. товара в год. Найти оптимальный размер партии (количество единиц товара в партии), оптимальное число поставок в год, оптимальную продолжительность цикла.

Решение. Поскольку общие издержки

,

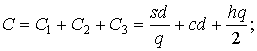
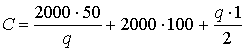тогда

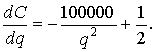
Приняв 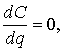получим 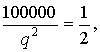откуда q² = 200000, и 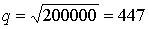ед. товара в партии.

Оптимальное число поставок в году:

n* =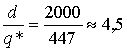

Оптимальная продолжительность цикла:

T* = 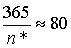дней.

Расчет оптимального размера партии в случае модели производственных поставок

Когда готовые товары доставляются на склад непосредственно с производственной линии, поступление не будет мгновенным. Дополнительный параметр – скорость производства р – равна количеству товаров, выпускаемых линией в течение года; спрос постоянен и равен d. Как только уровень запасов упадет до нуля с производственной линии начнет поступать товар на склад. Величина q – размер партии. График, отвечающий постановке задачи представлен на рис. 4.3.

Общие издержки в течение года, как и в предыдущей модели,

С = С₁ (общие затраты на организацию запаса) + С₂ (стоимость товара) + С₃ (общие затраты на хранение запасов).

При спросе d товаров в год одна поставка содержит q единиц товара, поэтому за год необходимо сделать n = d/q поставок, следовательно,

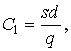С₂ = сd, С₃ = (средний уровень запасов)×n.

Для определения среднего уровня запасов используются следующие два обстоятельства:

1) максимальный уровень RT = (p – d)t;

2) количество единиц товара в одной поставке q = pt.

Тогда средний уровень запасов:

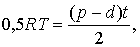но 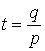, тогда средний уровень запасов 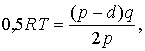а общие затраты на хранение запасов .

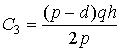Уравнение для общих годовых издержек:

С =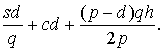

Приравняв 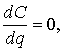получим 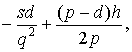откуда оптимальный размер партии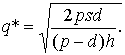

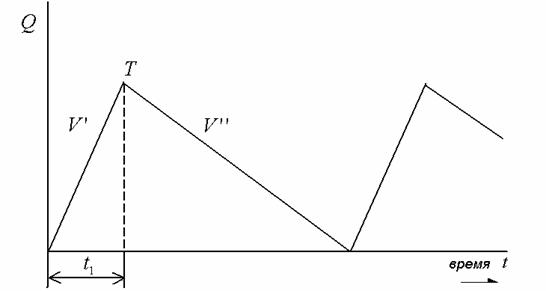
Рис. 4.3. Модель производственных поставок: Q – уровень запаса товаров;
t – время; RT – максимальный уровень запасов; t₁ – продолжительность

поставок; V’ – скорость пополнения запасов, равная p – d;

V”– постоянный спрос с интенсивностью d

Пример. При тех же данных: d = 2000 ед. товара в год, s = 50 у.е., c = 100 у.е., h = 1 у.е. за ед. товара, p = 4000 ед. товара в год, оптимальный размер партии составит

q* ≈ 633 ед. товара.

Оптимальное число партий в течение года

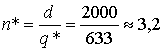парт.

Продолжительность поставки

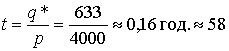дней.

Продолжительность цикла

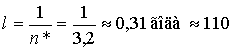дней.

Максимальный уровень запасов

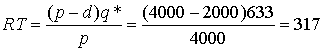ед. товара.

Средний уровень запасов

0,5RT = 0,5∙317 = 158 ед. товара.