При воздействии на систему множества факторов (оцениваемых количественно или качественно) устанавливается связь между ними и признаком. Факторы – независимые случайные переменные, признак – зависимая случайная переменная. В качестве характеристики изменения признака используется полная дисперсия. Задача дисперсионного анализа – разложение полной дисперсии на составляющие:
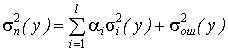 , (2.1)
, (2.1)
где 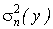 – полная дисперсия, характеризующая изменчивость признака у в данной серии экспериментов;
– полная дисперсия, характеризующая изменчивость признака у в данной серии экспериментов; 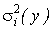 – cоставляющая полной дисперсии, обусловленная изменчивостью i-го фактора или взаимодействия факторов; αi – коэффициент, характеризующий объем наблюдений;
– cоставляющая полной дисперсии, обусловленная изменчивостью i-го фактора или взаимодействия факторов; αi – коэффициент, характеризующий объем наблюдений; 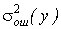 – дисперсия, характеризующая ошибку эксперимента и действие неучтенных факторов
– дисперсия, характеризующая ошибку эксперимента и действие неучтенных факторов
Для решения вопроса о том, существенно ли влияние данного фактора на признак, используется критерий Фишера:
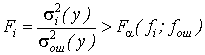 , (2.2)
, (2.2)
где α – уровень значимости, характеризующий вероятность, с которой определяется существенность исследуемого фактора; fi – число степеней свободы дисперсии 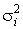 (у), характеризующее количество информации, использованное для ее вычисления; fош – число степеней свободы дисперсии
(у), характеризующее количество информации, использованное для ее вычисления; fош – число степеней свободы дисперсии 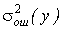 , характеризующее количество информации, использованное для ее определения, т.е. значимость оценивается на фоне шумового поля, создаваемого действием неучтенных факторов и ошибки эксперимента.
, характеризующее количество информации, использованное для ее определения, т.е. значимость оценивается на фоне шумового поля, создаваемого действием неучтенных факторов и ошибки эксперимента.
Модель однофакторного дисперсионного анализа
уik = μ + Ai + εik , (2.3)
где уik – значение признака у, когда фактор А находится на i-м уровне при k-м повторении опыта; μ – математическое ожидание признака у, оценка которого вычисляется по результатам всех наблюдений; Аi – влияние на изменчивость признака фактора А, когда он находится на i-м уровне (эффект фактора А); εik ошибка эксперимента и действие неучтенных факторов, когда фактор А находится на i-м уровне при k-м повторении опыта.
Для проведения анализа необходимо фактору А придавать различные значения, т. е. исследовать на различных уровнях i,
i = 2, 3,…, а; аmin = 2; k – число наблюдений на каждом уровне, k = 3, 4, …, n; kmin = 3. В случае однофакторного дисперсионного анализа общее число наблюдений N = a · n.
Проведя опыты, можно найти общую среднюю 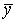 и средние значения по уровням наблюдений
и средние значения по уровням наблюдений 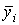 и определить суммарные квадраты.
и определить суммарные квадраты.
Q = 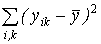 – полный суммарный квадрат, характеризующий полную изменчивость признака.
– полный суммарный квадрат, характеризующий полную изменчивость признака.
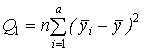 – суммарный квадрат, характеризующий отклонения групповых средних от общей средней, он определяет изменчивость признака от действия фактора А и межгрупповой ошибки эксперимента, число степеней свободы f1 = a – 1.
– суммарный квадрат, характеризующий отклонения групповых средних от общей средней, он определяет изменчивость признака от действия фактора А и межгрупповой ошибки эксперимента, число степеней свободы f1 = a – 1.
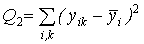 – суммарный квадрат, характеризующий ошибку эксперимента и действие неучтенных факторов внутри групп наблюдений.
– суммарный квадрат, характеризующий ошибку эксперимента и действие неучтенных факторов внутри групп наблюдений.
Поскольку опыты производятся в однородных условиях (это предпосылка проведения дисперсионного анализа), то межгрупповая дисперсия ошибки эксперимента и действия неучтенных факторов и общая дисперсия ошибки эксперимента и действия неучтенных факторов однородны. По сути, это одна и та же дисперсия, оценки которой вычисляются по разному объему выборок из одной и той же совокупности экспериментальных данных, поэтому ее оценка 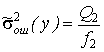 , где f2 – число степеней свободы, f2 = N – a. Учтя это и определив оценку дисперсии
, где f2 – число степеней свободы, f2 = N – a. Учтя это и определив оценку дисперсии 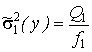 , можно записать
, можно записать
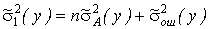 ,
,
откуда
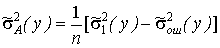 и
и 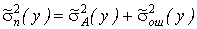 . (2.4)
. (2.4)
Вклад фактора в изменчивость признака вычисляется по формуле
Ввкл = [S2A(y)/S2п(у)]·100 %, (2.5)
где S2A(y), S2п(y) – соответственно оценка дисперсии, характеризующая вклад фактора в изменчивость признака, и полная дисперсия, характеризующая полную изменчивость признака.
Расчетные зависимости для рационального подсчета численных значений суммарных квадратов имеют вид
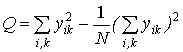 ;
; 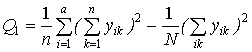 ;
;
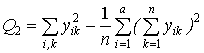 . (2.6)
. (2.6)
Пример. По данным источника [13] исследовать влияние местонахождения пункта продаж (Минск, Москва) на средние цены (тыс. долл США) легковых подержанных автомобилей марок БМВ, «Опель-Астра», «VW–Гольф», «Форд-Мондео» в ноябре 2000 г., имеющих в первом приближении одинаковое техническое состояние.
В табл. 13 приведены цены на автомобили в Минске и Москве, а также необходимые расчетные параметры.
Таблица 13
Вычисление показателей для расчета влияния местонахождения пункта продаж на средние цены подержанных автомобилей
| № п/п | Местонахождение пункта продаж | Суммы | |
| Минск | Москва | ||
| 1 | 2 | 3 | 4 |
| 1 | 5,0 | 6,8 | |
| 2 | 3,1 | 4,1 | |
| 3 | 2,3 | 5,0 | |
| 4 | 4,1 | 5,1 | |
| 5 | 5,3 | 7,2 | |
| 6 | 2,8 | 4,2 | |
| 1 | 2 | 3 | 4 |
| 7 | 3,4 | 5,4 | |
| 8 | 3,8 | 5,4 | |
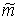 i i
| 3,7 | 5,4 | |
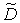 j j
| 1,1 | 1,2 | |
| Σу | 29,8 | 43,2 | 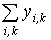 = 73 = 73
|
| Σу2 | 118,6 | 241,9 |
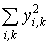 = 360,5 = 360,5
|
| (Σу)2 | 888,0 | 1866,2 | 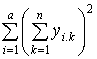 = 2754,2 = 2754,2
|
Решение. Приведенные значения параметров вычисляют по следующим формулам:
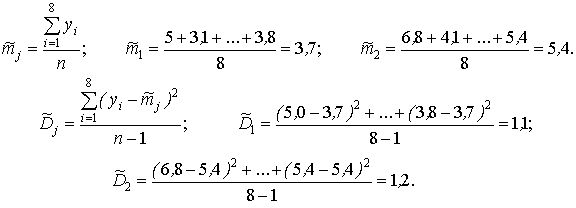
Вначале проверяют однородность оценок дисперсий по уровням наблюдений. Вычисляют значение F-статистики:
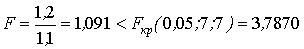 .
.
Следовательно, оценки дисперсий однородны, дисперсионный анализ можно проводить, поскольку с достаточным уровнем доверительной вероятности неучтенные факторы и неизбежная ошибка эксперимента существенно не повлияли на изменчивость признака.
Значения сумм для первого столбца данных (Минск):
Σу = 5,0 + 3,1 + …+ 3,8 = 29,8;
Σу2 = 5,02 + 3,12 +…+ 3,82 =118,6;
(Σу)2 = 29,82=888,0.
Для второго столбца (Москва):
Σу = 6,8 + 4,1 +…+ 5,4 = 43,2;
Σу2 = 6,82 + 4,12 +…+ 5,42 = 241,9;
(Σу)2 = 43,22 = 1866,2.
Для третьего столбца (суммы):
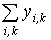 = 29,8 + 43,2 = 73;
= 29,8 + 43,2 = 73;
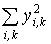 = 118,6 + 241,9 =360,5;
= 118,6 + 241,9 =360,5;
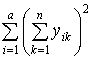 = 888,0 + 1866,2 =2754,2.
= 888,0 + 1866,2 =2754,2.
Вычисляют значения суммарных квадратов:
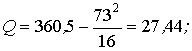
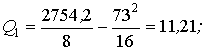
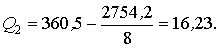
Оценка дисперсии, характеризующая изменение признака от воздействия фактора (местонахождения пункта продаж) и внутригрупповой ошибки эксперимента и действия неучтенных факторов при числе степеней свободы f1 = a – 1 = 2 – 1 = 1
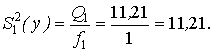
Оценка дисперсии, характеризующей воздействие на признак ошибки эксперимента и действия неучтенных факторов при числе степеней свободы f2 = N – a = 16 – 2 = 14
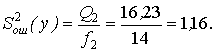
Значимость фактора (местонахождения пункта продаж) оценивается F-критерием при уровне значимости α = 0,05 и числах степеней свободы f1 = 1 и f2 = 14 (табл. 10 приложения), проверяется нулевая гипотеза Н0: S21(y) > S22(y) при конкурирующей Н1: S21(y) ≤ S22(y):
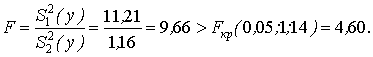
Поскольку значение F-статистики превышает критическое значение Fкр, гипотеза о существенности фактора не отвергается.
Значение оценки дисперсии S2А(у):
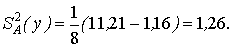
Величина оценки полной дисперсии
S2п (у) = 1,26 + 1,16 = 2,42.
Вклад фактора – местонахождения пункта продаж автомобилей – в формирование цены на подержанный автомобиль
Ввкл = (1,26 / 2,42)100% = 52 %.
Следовательно, цена на подержанный автомобиль на 52% зависит от места нахождения пункта продаж.
Дата: 2018-12-28, просмотров: 762.