Для оценки однородности средних значений независимых нормально распределенных величин, дисперсии которых равны (однородны), но неизвестны, может быть использован критерий Аббе, статистика которого задается отношением
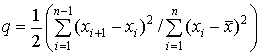. (1.18)
Проверяется нуль-гипотеза Н0: m*1(x) = m*2(x) = m*3(x) = m*4(x) при альтернативе Н1: |m*i+1 (x) – m*i (x)| > 0.
Если найденное значение q-статистики превышает критическое, то гипотеза о равенстве средних отвергается.
Пример 1. Требуется проверить гипотезу об однородности вкладов, приведенных в табл. 7, видов продукции в выручку от экспорта (данные по четырем федеральным округам РФ) в предположении, что известны только mi*(x) – средние значения выручки [17], а другой информации нет.
Таблица 7
Экспорт некоторых видов продукции России в 2000 г. по федеральным округам, млн долл
| Федеральные округа | Нефтехимические товары | Черные и цветные металлы | Машиностроительная продукция | Древесина и изделия из нее |
| Северо-западный | 3,0 | 2,3 | 1,5 | 1,6 |
| Южный | 1,6 | 0,6 | 0,4 | 0,0 |
| Сибирский | 2,3 | 5,7 | 0,5 | 1,0 |
| Дальневосточный | 1,0 | 0,3 | 0,6 | 0,5 |
| m*i (x) | 1,98 | 2,23 | 0,75 | 0,78 |
| D*i (x) | 0,7 | 6,1 | 0,3 | 0,5 |
Значения средних представляют в виде вариационного ряда: 0,75; 0,78; 1,98; 2,23, со средним 1,43 и вычисляют q-статистику:
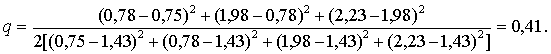
В соответствии с табл. 6 приложения значение q-статистики при n = 4 уровне значимости α = 0,05 составляет qкр = 0,3902 < q =
= 0,41, поэтому гипотеза о равенстве средних отвергается.
Следовательно, вклад в экспортную выручку различных видов продукции по указанным районам неодинаков: на первом месте – нефтехимические товары, на втором – черные и цветные металлы, и так далее.
Однако при вычислении q-статистики Аббе используется не вся информация об объектах, поэтому для парного сравнения средних используют критерий Стьюдента (табл. 7 приложения), тогда его статистика:
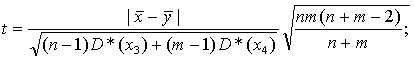(1.19)
где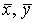 
– исследуемые средние значения; D*(x3), D*(x4) – оценки дисперсий случайных величин; n, m – объемы выборок; (n – 1),
(m – 1) – числа степеней свободы оценок дисперсий.
Проверяется нулевая гипотеза Н0: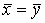 
при альтернативной Н1: 
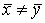при условии однородности оценок дисперсий и нормального распределения X и Y. Нулевая гипотеза отвергается, если |tнабл.| > tдвуст.кр (α/2; k), где a – уровень значимости, k – число степеней свободы, k = n + m – 2.
Пример 2. Оценить с помощью t-критерия однородность средних значений экспортной выручки для трех вариантов:
1) от машиностроительной продукции и древесины и изделий из нее при выполнении условия однородности оценок D*(x3) и D*(x4);
2) от нефтехимических товаров, черных и цветных металлов;
3) от нефтехимических товаров и древесины и изделий из нее.
Решение. 1. В соответствии с формулой
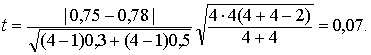
Найденное значение t-статистики меньше критического (табл. 7, приложения);
tнабл.= 0,07 < tдвуст.кр (0,1/2; 6) = 1,9432,
поэтому гипотеза о равенстве выручки по четырем районам РФ от машиностроительной продукции и от древесины и изделий из нее не отвергается.
2. Прежде, чем вычислить значение t-статистики для второго варианта, необходимо проверить однородность оценок дисперсий c помощью F-статистики (табл. 10 приложения):
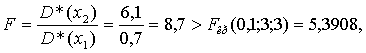
т. е. оценки дисперсий для исследуемых товаров X1 и X2 неоднородны, t-критерий не позволяет решать задачу об однородности m*(x1) и m*(x2).
3. Здесь очевидно, что оценки дисперсий однородны, значение t-статистики
,
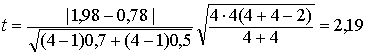поскольку tнабл. = 2,19 > tдвуст.кр (0,1/2; 6) = 1,9432 (табл. 7 приложения). Средние значения товаров X1 и X4 неоднородны, экспортная выручка от товаров нефтехимии больше, чем от древесины и изделий из нее. Все это согласуется с результатом, полученным при использовании критерия Аббе, который дает положительный ответ по поводу однородности средних значений только в случае, когда все средние однородны, но, если хотя бы одно значение неоднородно с каким–либо другим, то и ответ будет отрицательным.
Однородность средних для зависимых выборок проверяется с помощью d-статистики. Проверяется нулевая гипотеза
Н0 : М*(X) = M*(Y) при конкурирующей Н0: М*(X) ≠ M*(Y).
Пример 3. Средний балл успеваемости группы ИЭ-00 по математике в первом семестре по результатам экзаменационной сессии составил 3,43, во втором – 3,52, в третьем – 3,65, в четвертом – 3,74. Оценить однородность средних баллов, полученных студентами группы ИЭ-00 в 1-м и 4-м семестрах по математике во время экзаменационных сессий (табл. 8).
Таблица 8
Баллы, полученные студентами группы ИЭ-00 по математике в 1-м и 4-м семестрах
| Семестр | Балл | ||||||||||||||||||||||
| 1 | 3 | 3 | 3 | 3 | 3 | 4 | 3 | 3 | 3 | 5 | 3 | 4 | 3 | 4 | 3 | 3 | 3 | 5 | 4 | 4 | 3 | 3 | 4 |
| 4 | 4 | 3 | 3 | 3 | 4 | 5 | 3 | 3 | 4 | 4 | 3 | 4 | 3 | 4 | 4 | 3 | 3 | 5 | 4 | 5 | 4 | 3 | 5 |
Решение. Выборки зависимы, так как баллы 1-го и 4-го семестров в каждом столбце получены одним и тем же студентом и в силу этого являются попарно зависимыми.
Вычисляется среднее значение разностей баллов
d* = Σdi /n,
где di = xi – yi; xi, yi – баллы студентов, полученные ими в 1-м и 4-м семестрах соответственно, n – число студентов в группе.
d1 = 3 – 4 = – 1; d2 = 3 – 3 = 0;…; d5 = 3 – 4 = – 1;
d6 = 4 – 5 = – 1;…; d9 = 3 – 4 = – 1; d10 = 5 – 4 = 1;
d15 = 3 – 4 = – 1;…; d20 = 4 – 5 = – 1; d21 = 3 – 4 = – 1;
d22 = 3 – 3 = 0; d23 = 4 – 5 = –1.
Σdi = – 1 – 1 – 1 – 1 + 1 – 1 –1 – 1 – 1 = – 7;
d* = –7 / 23 = – 0,304.
Сумма квадратов разностей
Σd2i = (–1)2 + (–1)2 +(–1)2 + (–1)2 + (+1)2 + (–1)2 +(–1)2 + (–1)2 + (–1)2 = 9.
Среднее квадратическое отклонение разностей
Sd =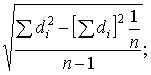 
Sd = 
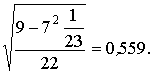
Наблюденное значение Т-статистики
Тнабл = d*n0,5/Sd = – 0,304·230,5/0,559 = – 2,6081.
Поскольку абсолютное значение Т-статистики больше, чем критическое значение tдвуст.кр.(0,10; 32) = 1,70 (табл. 7 приложения), средние баллы 1-го и 4-го семестров неоднородны, поэтому можно считать, что от 1-го к 4-му семестру имеет место небольшое, но значимое повышение успеваемости.
Дата: 2018-12-28, просмотров: 663.
