Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Расчет тяговых усилий сложен ввиду нелинейного характера зависимости потока от MDC.

В связи с этим вводятся различны допущения и упрощения.

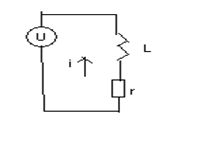
Для цепи обмотки (катушки) электромагнита следует справедливое уравнение баланса энергий:

Uidt = i ² rdt + wid Ф,

где U – электроэнергия от сети, i²r – потери в активном сопротивлении (на тепло), wi – энергия затрачиваемая на создание магнитного поля.

 

 

Переходя к конечным промежуткам, получим:

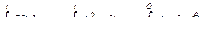
Для расчетов представляет интерес последний член, выражающий энергию магнитного поля.

Графически 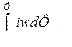можно представить площадью, заключенной между кривой намагничивания и осью ординат при неподвижном якоре.

 

 

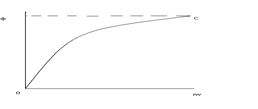
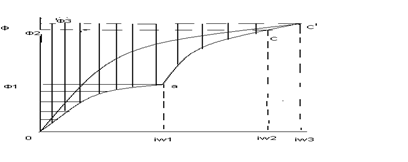
ОС – кривая с притянутым якорем

Оа – кр. намагн.

Оа – якорь неподвижен

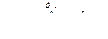 - пл. oaba  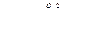- пл. bacdb

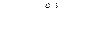 - пл. dcc’d  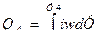- пл.

Т.о. энергия otcao из энергии поля переходит в механическую работу, затрачиваемую на движение якоря.                 Q _мех = Q ₁ + Q ₂ + Q ₃ - Q ₄

Эта энергия проявяется в виде работы сил электромагнитного притяжения, следовательно

F_эм= - (dQ_мех/d δ)

При расчете F_эм считаем, что рабоат материала магнитопровода происходит на линейном участке кривой намагничивания и что вся энергия магнитного поля сосредоточена в рабочем воздушном заторе, тогда

Q^вых_мех = iwФ/2 = (iw)²G/2

Откуда F_эм = -(iw)²/2 * (dG/d δ) = -1/2 * (Ф²/ μ₀S) = -1/2 * (B²S/ μ₀)

S – площадь

I – ток в катушке

Определение магнитной проводимости воздушного зазора.

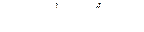
При 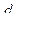 - погрешность 20%

Проинтегрируем:

 

 

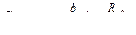
ЛЕКЦИЯ №31

Кулачковые механизмы

31.1. Основные сведения

Кулачковая передача состоит из кулачка и толкателя. Чаще ведущим кинематическим звеном кулачковой передачи явля­ется кулачок. Кулачковые передачи преобразуют движение кулачка в поступательное движение или качание толкателя. Кулачковые передачи находят широкое применение в приборных устройствах и машинах, в различных автоматических, счетно-решающих, рас­пределительных устройствах двигателей и станков-автоматов. Опе­рационные кулачковые передачи используют для зажима деталей, возврата стрелок шкальных приборов на ноль, замыкания элек­трических контактов в электрических переключателях и при обработке деталей по копиру, фиксации взаимного положения деталей и узлов. Функциональная кулачковая передача служит для воспроизведения заданной функции. Большинство функциональ­ных передач позволяет осуществить зависимость у = f (х). Пере­мещение кулачка, как и перемещение толкателя, может быть или линейным, или угловым.

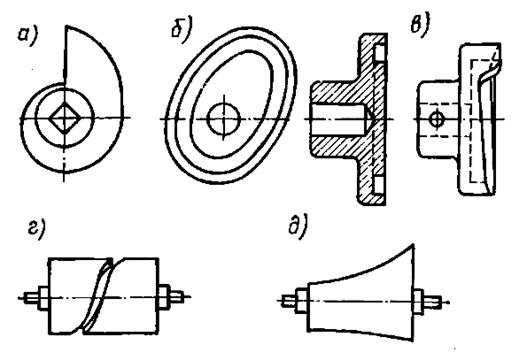
рис. 31.1

На рис. 31.1 показаны некоторые конструк­ции кулачков, которые применяются наиболее часто; а — плоский дисковый кулачок, б— торцовый кулачок с канавкой, в — тор­цовый кулачок без канавки, г — цилиндрический кулачок с канав­кой, д — коноид. Кулачковый механизм с коноидом позволяет осуществить зависимость z = f (х, y )_, где х пропорционально углу поворота коноида, у пропорционально перемещению коноида вдоль оси его вращения, z пропорционально перемещению толка­теля. Радиус-вектор коноида изменяется не только при его вра­щении, но и при перемещении вдоль оси вращения.

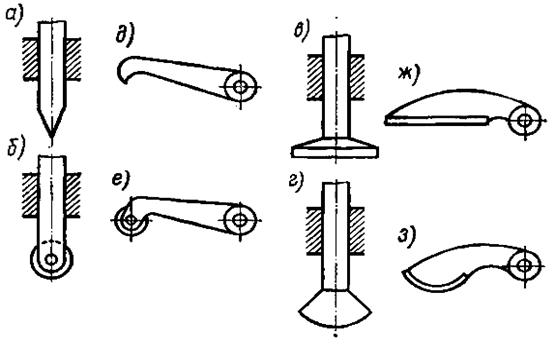
рис. 31.2

Заостренные толкатели (рис. 31.2, а, д) применяют только при небольших уси­лиях. Практически конец заостренного толкателя всегда имеет небольшое закругление. Часто используют толкатели, у которых имеется значительный радиус закругления конца (рис. 31.2, г, з), а также плоские толкатели (рис. 31.2, в, ж). Плоский толкатель работает с выпуклым кулачком. При роликовых толкателях между кулачком и толкателем действует трение качения (рис. 31.2, б, е). Благодаря этому уменьшаются трение и износ. Толкатели на рис. 31.2, а...г двигаются поступательно, а толкатели на рис. 31.2, д...з поворачиваются.

Кулачковые передачи могут иметь силовое или кинематическое замыкание. При силовом замыкании толка­тель прижимается к кулачку пружиной. На рис. 31.4, а - ж представлены различные вариации кулачковых механизмов с силовым замыканием, где обозначены:

 1 — кулачок, 2 — толкатель, 3 — пружина.

 

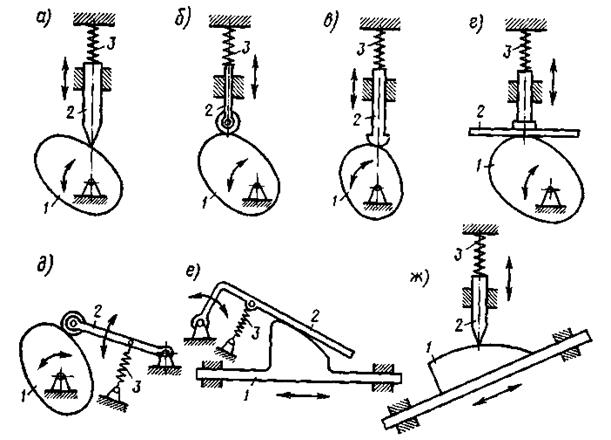
рис. 31.4

 

При кинематическом замыкании кулачкового механизма отпадает необходимость в пружине. Схемы кулачковых механизмов с кине­матическим замыканием кинематической цепи показаны на рис. 31.5. При повороте торцового кулачка с канавкой (рис. 31.5, а) роли­ковый толкатель перемещается вверх или вниз вдоль своей на­правляющей, а ролик не выходит из канавки кулачка. Двойной дисковый кулачок (рис. 31.5, б) поворачивается относительно своей оси, вызывая угловое перемещение толкателя-коромысла. Ролики коромысла непрерывно касаются каждый своего кулачка. Поэтому профили обоих кулачков должны соответствовать один другому, что обеспечивается их построением. Хотя каждый из дисковых кулачков вместе со своим роликом составляет кулачковый меха­низм, требующий силового замыкания кинематической цепи, но их одновременное действие создает надежное кинематическое замыкание. При повороте цилиндрического кулачка с канавкой толкатель либо поворачивается (рис. 31.5, в), либо перемещается поступательно вдоль направляющей (рис. 31.5, г).

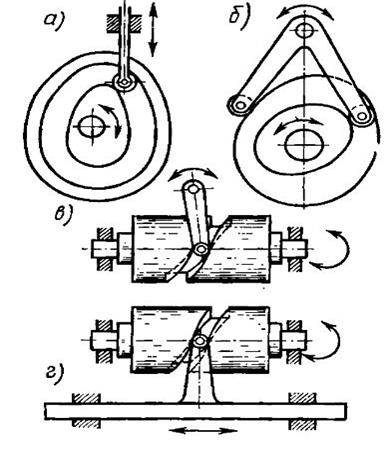
рис. 31.5

 

31.2 Кинематика кулачковых передач

 

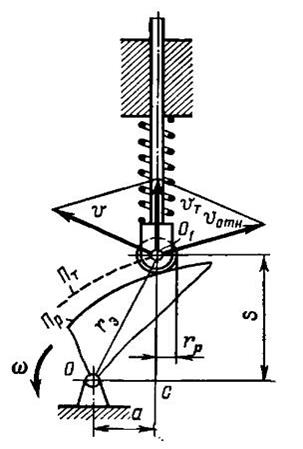
рис. 31.6

На рис. 31.6 показана кулачковая передача с поступательно перемещающимся дезаксиальным роликовым толкателем. Дезаксиальной эта передача называется пото­му, что средняя линия толкателя не про­ходит через геометрическую ось враще­ния кулачка О. Имеет место дезаксиал а = OC, причем OC перпендикулярно CO₁. Кулачок вращается с угловой ско­ростью w. При этом геометрическая ось вращения ролика О₁ перемещается по прямой вверх и все время находится на штриховой кривой, которая называется теоретическим профилем кулачка П_т. Длина пути s, проходимая толкателем, равна перемещению точки О₁. Условно отсчитываем ее от точки С:   ,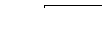

где r _э  — радиус-вектор теоретического профиля П_т кулачка.

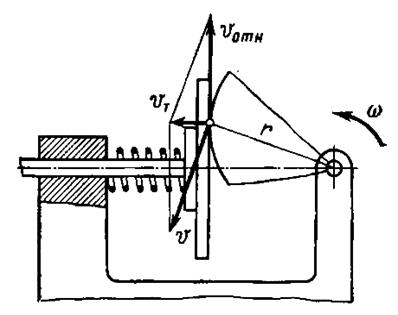
рис. 31.7

На рис. 31.7 построен план скоростей для центральной кулач­ковой передачи с дисковым кулачком и поступательно перемещаю­щимся плоским толкате­лем. Окружная скорость кулачка перпендикулярна радиус-вектору r кулачка:

v = w r

Относительная скорость v_отн, направлена по общей касательной, проведенной к поверхно­стям кулачка и толкателя в точке их касания. В данном случае она со­впадает по направлению с плоскостью толкателя. Скорость толкателя v_т на­правлена вдоль оси направляющей.

 

рис. 31.8

На рис. 31.8 показан план скоростей в кулачковом механизме с качающимся толкателем. Толкатель роликовый. Геометрическая ось вращения С ролика находится на теоретическом профиле П_т, кулачка. Реальный профиль П_р кулачка по отношению к теорети­ческому является эквидистантной кривой. Окружная скорость v перпендикулярна ради­ус-вектору r_э, а относи­тельная скорость v_отн касательна к теоретиче­скому профилю в точке С. Окружная скорость v_т толкателя перпенди­кулярна прямой O ₂ C .

 

Программные механизмы

Кулачковые механизмы часто используют для смыкания и размыкания контактов. Программные механизмы обеспечивают размыкание групп контактов по определённой, заранее установленной, программе по времени. Набор кулачков из текстолита, установленных на общем валу, вращается с постоянной угловой скоростью w. Если кулачковый программный механизм совершает несколько оборотов, то программы повторяются. В этом случае программу указывают только для одного оборота и называют циклограммой. Заштрихованные участки соответствуют периодам замыкания, по горизонтали откладывается время (t), по вертикали количество кулачков (n).

 

 

 

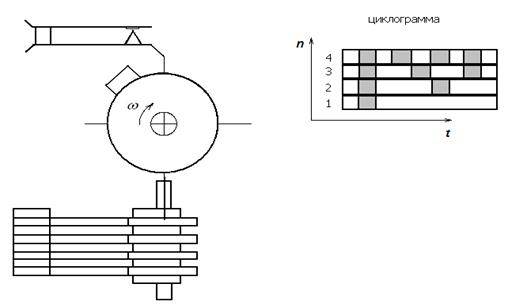
Силы в кулачковых передачах

На рис. 31.9 показаны силы в дезаксиальной кулачковой пере­даче с поступательно перемещающимся толкателем. Угол b между осевой линией толкателя и радиус-вектором, проведенным через точку касания толкателя и кулачка, называют углом толкателя. В общем случае угол b — переменная величина. Угол между линией действия силы F , приложенной к толкателю, и нормалью пп к поверхности кулачка в точке касания с толкателем называют углом давления a. Угол q меж­ду направлением радиус-вектора и нормалью к поверхности кулач­ка или линией действия нормаль­ной силы F_n для той же точки на­зывается углом кулачковой пере­дачи или углом подъема кулачка.

Из треугольника ABE (рис. 31.10) получим формулу для опре­деления угла передачи:

tg q  = dr / ( rd g ),

где g — Угол поворота радиус-вектора кулачка.

 

 

 

 

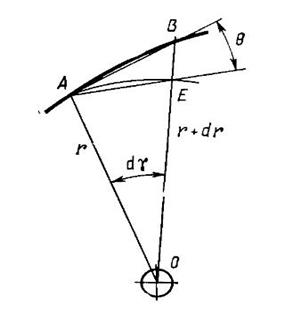
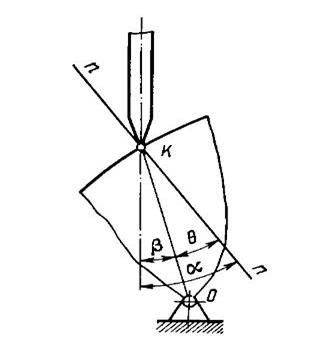
Треугольник ABE весьма бли­зок к прямоугольному, причем угол ВЕА равен 90°. В этом лег­ко убедиться, если учесть, что угол d g — бесконечно малая ве­личина. Угол передачи может быть образован также касатель­ной к поверхности кулачка и пер­пендикуляром к радиус-вектору, проведенному через точку каса­ния. Из рис. 31.9 следует q = a ± b. Знак минус принимают, когда точка О находится правее линии действия силы F (рис. 31.11).

Для центрального кулачкового механизма

b = 0 и q = a

 угол передачи в этом случае равен углу давления. Если не учитывать трения, то сила F, действующая на толкатель, вызовет нормальное давление

F_n = F / cos a

 Сила трения, действующая на толкатель, равна

F_тр = f F_n

 Равнодействующей сил F_n и F_тр является сила F_р. Угол между силами F_p и F_n равен углу трения j:                f = tg j ,

где f — коэффициент трения между кулачком и толкателем. Увели­чение угла давления при заданной силе F вызывает увеличение нормального давления F_n ,что способствует увеличению износа и потерь от трения. Сила F_р , действующая на толкатель, преодоле­вает силу пружины F и сопротивления от трения в направляющей. При значительных нагрузках реакции F ₁ и F ₂ возникают у краев направляющей. Они вызывают появление сил трения F_трl = f₁  F₁ ;  F_тр2 = f₁ F₂ ,

где f ₁ — коэффициент трения между толкателем и направляющей.

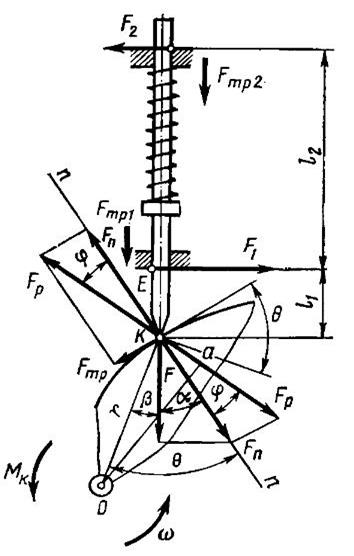
рис. 31.9

рис. 31.10                                               рис. 31.11

 

На рис. 31.3, а, б показано крепление роликов с подшипниками скольжения, на рис. 31.3, в, г — крепление роли­ков с подшипниками качения. Когда толкатель находится во взаи­модействии с коноидом, то его конец имеет сферическую форму (рис. 31.3, д, е). Толкатель на рис. 8.3, д скользит по коноиду, а толкатель на рис. 31.3, е закреплен на подшипниках качения.

 

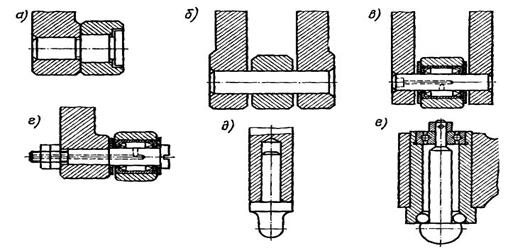
рис. 31.3

ЛЕКЦИЯ № 27