Подвижную систему прибора можно представить в виде колебательной системы, состоящей из массы m, упругого элемента с жесткостью с и успокоителя с коэффициентом успокоения k.
Подвижная система 1 выведена из равновесия и совершает колебания относительно неподвижного корпуса 2.
рис.1.
Уравнение движения подвижной системы с линейным движением успокоителя имеет вид: 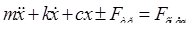 , (1)
, (1)
где 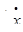 - смещение массы относительно положения равновесия,
- смещение массы относительно положения равновесия,
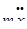 - инерционная сила,
- инерционная сила, 
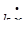 - сила успокоения,
- сила успокоения,
cx – сила упругости,
F тр - сила сухого трения,
F внеш - сила внешнего воздействия.
Силу сухого трения F тр подбором опор подвижной системы минимизируют, так как она снижает чувствительность прибора. Поэтому при решении уравнения (1) силой F тр можно пренебречь. Внешнюю силу F внеш можно уменьшить с помощью амортизаторов или она может просто отсутствовать.
Тогда уравнение приобретает вид:
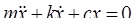 . (2)
. (2)
При отсутствии успокоения (с = 0) решение уравнения имеет вид:
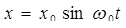 ,
,
где 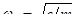 - частота собственных колебаний.
- частота собственных колебаний.
В приведенном виде уравнение (2) имеет вид:
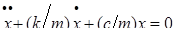
Обозначим k / m =2ε и 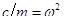 .
.
Тогда уравнение собственных колебаний подвижной системы можно записать в виде:
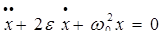 , (3)
, (3)
где ε - половина удельного коэффициента успокоения.
Решение уравнения:
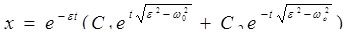 ,
,
где С1 и С2 – постоянные интегрирования, определяемые из начальных условий.
При анализе решения (3) рассмотрим три случая:
· ε = ω0 - критическое успокоение;
· ε > ω0 - лимитационное движение;
· ε < ω0 - колебательное движение.
Для сравнения движения механической системы ПУ с использованием успокоителя и движения прибора в режиме критического успокоения вводится параметр степень успокоения:
D = k / k кр =ε/εкр= ε/ ω0.
Степенью успокоения называют величину, равную отношению системы прибора k , который имел бы место быть при режиме критического успокоения той же системы kкр. В точных приборах в основном применяется режим со степенью успокоения меньше единицы.
В этом случае (D<1 или ε < ω0) решение уравнения (3 )(рис.1):
x= x0e-εtsin(Θt+γ),
где Θ=(ω02-ε2)-2, x0 - начальный размах колебаний;
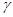 - начальная фаза колебаний; Т - период успокоения, Т=2π/Θ.
- начальная фаза колебаний; Т - период успокоения, Т=2π/Θ.
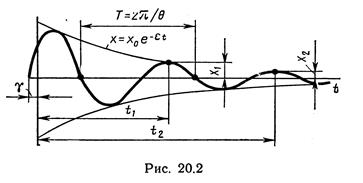
Как видно из графика, свободные колебания затухают по закону экспоненты. Очевидно, что чем сильнее успокоение в системе, тем интенсивнее уменьшается размах колебаний, т.е. тем скорее «успокаивается» система. Затухание колебаний можно характеризовать коэффициентом затуханий колебаний или декрементом (убавлением) колебаний  .
.
Декремент затухания  , которым называют отношение предыдущей амплитуды
, которым называют отношение предыдущей амплитуды 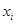 колебания к последующей
колебания к последующей 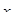 , т.е.
, т.е.
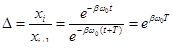 .
.
Наряду с декрементом затухания  в расчетах используют логарифмический декремент затухания
в расчетах используют логарифмический декремент затухания
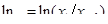 .
.
Связь декремента колебаний со степенью успокоения:
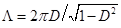 .
.
Как другой пример, рассмотрим работу электроизмерительного прибора, схема которого приведена на рисунке .
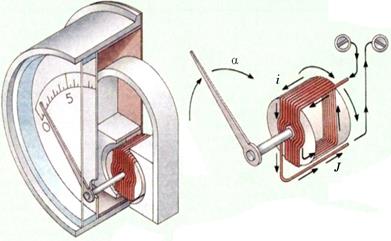
рис. 2
К виткам обмотки на рамке с помощью подвижных контактов подается напряжение. При взаимодействии рамки с обмоткой и магнитного поля от постоянного магнита, рамка поворачивается. Рамка имеет момент инерции Ј. Уравнение движения подвижной части прибора на основании принципа Д’Аламбера можно записать в следующем виде:
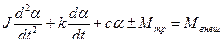
| (1) |
где α – угол поворота подвижной системы;
M внеш – внешний момент, действующий на подвижную систему;
M тр – момент трения в подвижной системе;
c ·α – противодействующий момент со стороны пружины;
c – жесткость пружины;
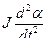 – момент сил инерции или инерционный момент;
– момент сил инерции или инерционный момент;
Ј – момент инерции подвижной системы относительно оси вращения;
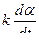 – момент, создаваемый успокоителем;
– момент, создаваемый успокоителем;
k – коэффициент успокоения (численно равный моменту успокоения, при угловой скорости подвижной системы 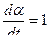 ).
).
Рассмотрим 2 частных случая движения механической системы при M внеш = 0, Мтр = 0, (рис. ).
Случай 1
Допустим, что в ПУ не установлен успокоитель, тогда уравнение примет вид:
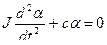 или
или 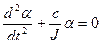
Решение уравнения имеет вид:
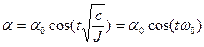 , ,
| (2) |
где α0 – угол отклонения системы от начального положения равновесия
при t = 0 и 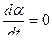 ;
; 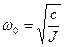 – круговая частота собственных колебаний.
– круговая частота собственных колебаний.
Из выражения (2) видно, что если систему вывести из состояния равновесия на угол α0, то она будет совершать незатухающие колебания по косинусному закону. График приведен на рисунке 3.
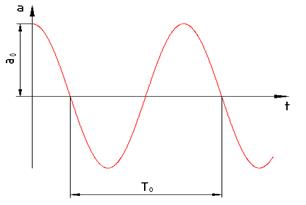
рис. 3
Период собственных незатухающих колебаний равен:
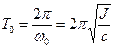
Очевидно, что чем больше момент инерции J и меньше жесткость упругого элемента c, тем больше Т0.
Частота собственных незатухающих колебаний будет в этом случае равна:
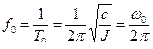
Наибольшее отклонение системы за период Т0 - амплитуда колебаний равная 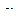 .
.
Случай 2
Рассмотрим случай, когда успокоитель в ПУ установлен. Тогда уравнение (1) будет иметь вид
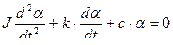
| (3) |
Характер движения подвижной системы прибора полностью определяется степенью успокоения (демпфирования) 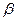 и круговой частотой собственных колебаний
и круговой частотой собственных колебаний 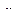 . Величина
. Величина 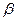 определяется по формуле:
определяется по формуле:
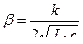 – степень успокоения (демпфирования)
– степень успокоения (демпфирования)
Если умножить 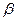 на
на 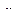 :
:
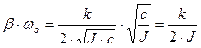 ,
,
то коэффициент успокоения k можно записать как:
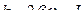 .
.
Тогда, в приведенном виде исходное уравнение (3) имеет вид:
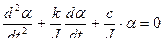
или
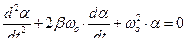
Рассмотрим влияние 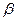 и
и 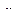 на характер движения подвижной системы рассмотрев три варианта:
на характер движения подвижной системы рассмотрев три варианта:  ;
;  ;
;  .
.
1. При  решение имеет вид:
решение имеет вид:
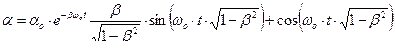
| (4) |
Из решения (4) видно, что с течением времени амплитуда колебаний будет убывать, т.е. колебания будут затухающими (рис. 4).
рис. 4
Установившейся считают подвижную систему, если колебания относительно положения равновесия не превосходят малой наперед заданной величины  , измеряемой в радианах. Для упрощения введен коэффициент
, измеряемой в радианах. Для упрощения введен коэффициент 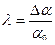 , характеризующий относительную точность установки системы в положение равновесия.
, характеризующий относительную точность установки системы в положение равновесия.
Время в течение, которого подвижная система приходит в положение равновесия, называют временем успокоения 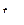 .
.
Из сравнения выражений (2) и (4) следует, что введение в систему успокоителя изменило частоту колебаний системы:
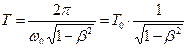
Таким образом, при 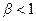 период
период 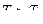 и по мере приближения
и по мере приближения 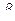 к единице, период
к единице, период  приближается к бесконечности, а колебания системы к апериодическому движению.
приближается к бесконечности, а колебания системы к апериодическому движению.
Для определения быстроты затухания колебаний вводится дополнительно характеристика - декремент затухания  , которым называют отношение предыдущей амплитуды
, которым называют отношение предыдущей амплитуды  колебания к последующей
колебания к последующей  , т.е.
, т.е.
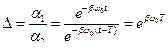 .
.
Наряду с декрементом затухания  в расчетах используют логарифмический декремент затухания
в расчетах используют логарифмический декремент затухания 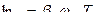 .
.
2. При 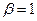 решение примет вид:
решение примет вид:
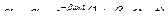
| (5) |
Режим колебаний при 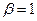 называется критическим режимом. В этом режиме в системе нет колебаний, и она долго подходит к положению равновесия (кривая 1 на рис. 5).
называется критическим режимом. В этом режиме в системе нет колебаний, и она долго подходит к положению равновесия (кривая 1 на рис. 5).
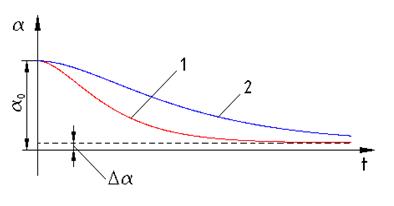
рис. 5
3. Решение при 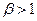 .
.
В этом случае также нет колебаний в системе, но система будет еще медленнее приближаться к положению равновесия (кривая 2 на рис. 5). В целом движение системы при 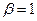 и
и 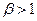 к положению равновесия называется апериодическим. Вывод: чем больше
к положению равновесия называется апериодическим. Вывод: чем больше 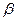 , тем медленнее система движется к состоянию покоя.
, тем медленнее система движется к состоянию покоя.
Вернемся к случаю, когда 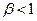 - это наиболее часто встречающийся на практике случай.
- это наиболее часто встречающийся на практике случай.
Подставив значение Т в выражение для  , получаем:
, получаем:
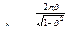
Из этого выражения видно, что, задаваясь величиной степени успокоения 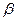 , можно определить декремент затухания
, можно определить декремент затухания  , а случае когда в приборе необходимо обеспечить определенный декремент затухания
, а случае когда в приборе необходимо обеспечить определенный декремент затухания  , то необходимая величина степени успокоения
, то необходимая величина степени успокоения 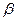 может быть подсчитана по формуле:
может быть подсчитана по формуле:
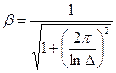
При расчете времени успокоения 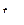 чаще всего пользуются коэффициентом
чаще всего пользуются коэффициентом 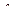 .
.
Время успокоения 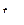 подсчитывается по формуле:
подсчитывается по формуле:
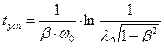
или
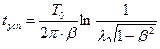
Итак, для расчета успокоителя должны быть заданы 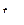 , J , c,
, J , c, 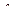 .
.
Дата: 2019-02-02, просмотров: 511.