Исследование температуры, возникающей в зоне резания

Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Рассмотрим методику получения зависимости температуры 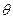резания от скорости υ, подачи s и глубины резания t при обработке точением стали 20 цельными проходными резцами из быстрорежущей стали Р18 [3].

Эмпирические температурные зависимости часто представляют уравнениями регрессии вида

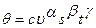. (4.33)

Уравнение (4.33) после логарифмирования получит вид

. (4.34)

Решено представить результаты эксперимента полиномом второй степени:

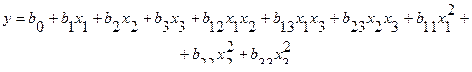, (4.35)

где 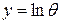; θ – температура; 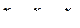– кодированные значения факторов υ, s, t.

В качестве плана эксперимента использовали центральный композиционный ротатабельный план второго порядка.

Кодирование независимых переменных производили с помощью соотношения (4.23).

Принятые в исследовании уровни факторов указаны в табл.4.14.

Таблица 4.14

Уровни факторов

Уровни факторов	υ,м/с .	x₁	s, мм/об	x₂	t, мм	х₃
Верхнее «звездное плечо»:	0,725	1,682	0,463	1,682	1,49	1,682
Верхний уровень	0,454	1	0,26	1	1,04	1
Основной уровень	0,229	0	0,17	0	0,61	0
Нижний уровень	0,115	–1	0,11	–1	0,36	–1
Нижнее «звездное плечо»	0,072	–1,682	0,082	–1,682	0,25	–1,682

Формулы преобразования натурных значений факторов кодированные в данном случае имеют вид [3]

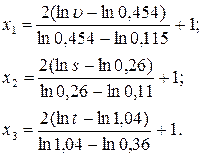(4.36)

Матрица планирования и результаты опытов представлены в табл.4.15.

В результате расчетов коэффициентов получено следующее уравнение регрессии:

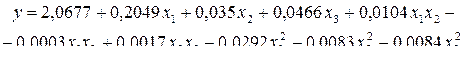(4.37)

Дисперсию воспроизводимости вычисляли по результатам шести опытов в центре плана .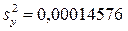

Дисперсии коэффициентов уравнения регрессии, полученные в режиме расчетов,

;

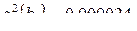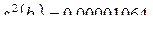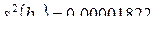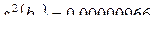Доверительные интервалы коэффициентов при 5.% -ном уровне значимости:

;

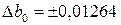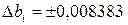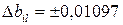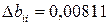Коэффициенты b₁₂, b₁₃, b₂₃ по абсолютной величине меньше доверительного интервала, поэтому их можно считать статистически незначимыми и исключить из уравнения регрессии.

После исключения незначимых коэффициентов уравнение (4.37) получило вид

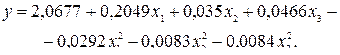(4.38)

Проверка гипотезы адекватности модели, представленной уравнением (4.38), показала, что модель адекватна при 5%-ном уровне значимости, так как F_P < F_T.

Таблица 4.15

Матрица планирования и результаты опытов

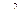
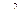
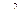
Номер опыта	x₀	x₁	x₂	x ₃	x₁ x₂	x₁ x ₃	x ₂ x ₃				y
1	+	–	–	–	+	+	+	+	+	+	1,6879
2	+	+	–	–	–	–	+	+	+	+	2,0777
3	+	–	+	–	–	+	–	+	+	+	1,8499
4	+	+	+	–	+	–	–	+	+	+	2,2837
5	+	–	–	+	+	–	–	+	+	+	1,7787
6	+	+	–	+	–	+	–	+	+	+	2,1677
7	+	–	+	+	–	–	+	+	+	+	1,9479
8	+	+	+	+	+	+	+	+	+	+	2,3801
9	+	–1,682	0	0	0	0	0	2,829	0	0	1,6391
10	+	+1,682	0	0	0	0	0	2,829	0	0	2,3311
11	+	0	–1,682	0	0	0	0	0	2,829	0	1,8868
12	+	0	+1,682	0	0	0	0	0	2,829	0	2,2016
13	+	0	0	–1,682	0	0	0	0	0	2,829	1,9652
14	+	0	0	+1,682	0	0	0	0	0	2,829	2,1226
15	+	0	0	0	0	0	0	0	0	0	2,0551
16	+	0	0	0	0	0	0	0	0	0	2,0734
17	+	0	0	0	0	0	0	0	0	0	2,0743
18	+	0	0	0	0	0	0	0	0	0	2,0568
19	+	0	0	0	0	0	0	0	0	0	2,0608
20	+	0	0	0	0	0	0	0	0	0	2,0858

Это свидетельствует о том, что исследуемый процесс не может быть описан уравнением (4.33). Уравнение (4.38) для рассматриваемой области изменения факторов дает возможность предложить другую модель процесса. Эту модель получим, подставив в уравнение (4.38) вместо кодированных натуральные значения факторов, используя для этого соотношения (4.36).

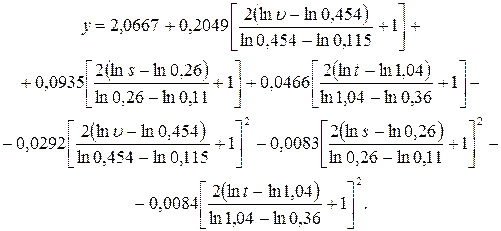
После преобразования получена зависимость

, (4.39)

которая позволяет определять температуру резания в достаточно широком диапазоне изменения режимов резания при обработке точением стали 20. По уравнению (4.39) может быть построена номограмма, которая позволит в практических условиях определять температуру резания при выбранных значениях элементов режима резания.

Рассмотренные в настоящем учебном пособии теоретические вопросы, связанные с планированием и реализацией многофакторных экспериментов, приведенные конкретные примеры применения изложенной методологии применительно к различным процессам механической обработки деталей способствуют освоению читателями процедуры постановки, проведения многофакторных экспериментальных исследований, статистической обработки результатов и проверки полученных моделей на адекватность, что несомненно повысит научно – технический уровень проводимых исследований.

Для реализации экстремальных планируемых многофакторных экспериментов необходимо использовать статистические данные, содержащиеся в таблицах 1-5, приведенных в приложении.

ПРИЛОЖЕНИЕ. Таблицы математической статистики.

Таблица 1

Значения t – критерия Стьюдента

(q – уровень значимости; f – число степеней свободы).

f	q		f	q		f	q
f	0,05	0,01	f	0,05	0,01	f	0,05	0,01
1 2 3 4 5 6 7 8 9 10 11 12 13	12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16	63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 3,01	14 15 16 17 18 19 20 21 22 23 24 25 26	2,14 2,13 2,12 2,11 2,10 2,09 2,09 2,08 2,07 2,07 2,06 2,06 2,06	2,98 2,95 2,92 2,90 2,88 2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78	27 28 29 30 40 50 60 80 100 120 200 500 ∞	2,05 2,05 2,05 2,04 2,02 2,01 2,00 1,99 1,98 1,98 1,97 1,96 1,96	2,77 2,76 2,76 2,75 2,70 2,68 2,66 2,64 2,63 2,62 2,60 2,59 2,58

Таблица 2

Значения F- критерия Фишера.

(f1- число степеней свободы большой дисперсии; f2-число степеней свободы меньшей дисперсии).

f2	f1
f2	1	2	3	4	5	6	7	8	9	10	12	15	20	30	∞
q=0,05
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24	161 18,51 10,13 7,71 6,61 5,59 5,59 5,32 5,12 4,96 4,84 4,75 4,67 4,60 4,54 4,49 4,45 4,41 4,38 4,35 4,32 4,30 4,28 4,26	200 19,00 9,55 6,94 5,79 5,14 4,74 4,46 4,26 4,10 3,98 3,89 3,81 3,74 3,68 3,63 3,59 3,55 3,52 3,49 3,47 3,44 3,42 3,40	216 19,16 9,28 6,59 5,41 4,76 4,35 4,07 3,86 3,71 3,59 3,49 3,41 3,34 3,29 3,24 3,20 3,16 3,13 3,10 3,07 3,05 3,03 3,01	225 19,25 9,12 6,39 5,19 4,53 4,12 3,84 3,63 3,48 3,36 3,26 3,18 3,11 3,06 3,01 2,96 2,93 2,90 2,87 2,84 2,82 2,80 2,78	230 19,30 9,01 6,26 5,05 4,39 3,97 3,69 3,48 3,33 3,20 3,11 3,03 2,96 2,90 2,85 2,81 2,77 2,74 2,71 2,68 2,66 2,64 2,62	234 19,33 8,94 6,16 4,95 4,28 3,78 3,58 3,37 3,22 3,09 3,00 2,92 2,85 2,79 2,74 2,70 2,66 2,63 2,60 2,57 2,55 2,53 2,51	237 19,35 8,89 6,09 4,88 4,21 3,79 3,50 3,29 3,14 3,01 2,91 2,83 2,76 2,71 2,66 2,61 2,58 2,54 2,51 2,49 2,46 2,44 2,42	239 19,37 8,85 6,04 4,82 4,15 3,73 3,44 3,23 3,07 2,95 2,85 2,77 2,70 2,64 2,59 2,55 2,51 2,48 2,45 2,42 2,40 2,37 2,36	241 19,38 8,81 6,00 4,77 4,10 3,68 3,39 3,18 3,02 2,90 2,80 2,71 2,65 2,59 2,54 2,49 2,46 2,42 2,39 2,37 2,34 2,32 2,25	242 19,40 8,79 5,94 4,74 4,06 3,64 3,35 3,14 2,98 2,85 2,75 2,67 2,60 2,54 2,49 2,45 2,41 2,38 2,35 2,32 2,30 2,27 2,25	244 19,41 8,74 5,91 4,68 4,00 3,57 3,28 3,07 2,91 2,79 2,69 2,60 2,53 2,48 2,42 2,38 2,34 2,31 2,28 2,25 2,23 2,20 2,18	246 19,43 8,70 5,86 4,62 3,94 3,51 3,22 3,01 2,85 2,72 2,62 2,53 2,46 2,40 2,35 2,31 2,27 2,23 2,20 2,18 2,15 2,13 2,11	248 19,45 8,66 5,80 4,56 3,87 3,44 3,15 2,94 2,77 2,65 2,54 2,46 2,39 2,33 2,28 2,23 2,19 2,16 2,12 2,10 2,07 2,05 2,03	250 19,46 8,62 5,75 4,50 3,81 3,38 3,08 2,86 2,70 2,57 2,47 2,38 2,31 2,25 2,19 2,15 2,11 2,07 2,04 2,01 1,98 1,96 1,94	254 19,50 8,53 5,63 4,36 3,67 3,23 2,93 2,71 2,54 2,40 2,30 2,21 2,13 2,07 2,01 1,96 1,92 1,88 1,84 1,81 1,78 1,76 1,73

Продолжение табл.2

f2	f1
f2	1	2	3	4	5	6	7	8	9	10	12	15	20	30	∞
25 26 28 29 30 40 60 120 ∞	4,24 4,23 4,21 4,20 4,18 4,17 4,08 4,00 3,92 3,84	3,39 3,37 3,35 3,34 3,33 3,32 3,23 3,15 3,07 3,00	2,99 2,98 2,96 2,95 2,93 2,92 2,84 2,76 2,68 2,60	2,76 2,74 2,73 2,71 2,70 2,69 2,61 2,53 2,45 2,37	2,60 2,59 2,57 2,56 2,55 2,53 2,45 2,37 2,29 2,21	2,49 2,47 2,46 2,45 2,43 2,42 2,34 2,25 2,17 2,10	2,40 2,39 2,37 2,36 2,35 2,33 2,25 2,17 2,09 2,01	2,34 2,32 2,31 2,29 2,28 2,27 2,18 2,10 2,02 1,94	2,28 2,27 2,25 2,24 2,22 2,21 2,12 2,04 1,96 1,88	2,24 2,22 2,20 2,19 2,18 2,16 2,08 1,99 1,91 1,83	2,16 2,15 2,13 2,12 2,10 2,09 2,00 1,92 1,83 1,75	2,09 2,07 2,06 2,04 2,03 2,01 1,92 1,84 1,75 1,67	2,01 1,99 1,97 1,96 1,94 1,93 1,84 1,75 1,66 1,57	1,92 1,90 1,88 1,87 1,85 1,84 1,74 1,65 1,55 1,46	1,71 169 1,67 1,65 1,64 1,62 1,51 1,39 1,25 1,00
q = 0.01
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17	4052 98,50 34,12 21,20 16,26 13,75 12,25 11,26 10,56 10,04 9,65 9,33 9,07 8,86 8,68 8,53 8,40	4999 99,00 30,82 18,00 13,27 10,92 9,55 8,65 8,02 7,56 7,21 6,93 6,70 6,51 6,36 6,23 6,11	5403 99,17 29,46 16,69 12,06 9,78 8,45 7,59 6,99 6,55 6,22 5,95 5,74 5,56 5,42 5,29 5,18	5625 99,25 28,71 15,98 11,39 9,15 7,85 7,01 6,42 5,99 5,67 5,41 5,21 5,04 4,89 4,77 4,67	5764 99,30 28,42 15,52 10,97 8,75 7,46 6,63 6,06 5,64 5,32 5,06 4,86 4,69 4,56 4,44 4,34	5859 99,33 27,91 15,21 10,67 8,47 7,19 6,37 5,80 5,39 5,07 4,82 4,62 4,46 4,32 4,20 4,10	5928 99,36 27,67 14,98 10,46 8,26 6,99 6,18 5,61 5,20 4,89 4,64 4,44 4,28 4,14 4,03 3,93	5982 99,37 27,49 14,80 10,29 8,10 6,84 6,03 5,47 5,06 4,74 4,50 4,30 4,14 4,00 3,89 3,79	6022 99,39 27,35 14,66 10,16 7,98 6,72 5,91 5,35 4,94 4,63 4,39 4,19 4,03 3,89 3,78 3,68	6056 99,40 27,23 14,55 10,05 7,87 6,62 5,81 5,26 4,85 4,54 4,30 4,10 3,94 3,80 3,69 3,59	6106 99,42 27,05 14,37 9,89 7,72 6,47 5,67 5,11 4,71 4,40 4,16 3,96 3,80 2,67 3,55 3,46	6157 99,43 26,87 14,20 9,72 7,56 6,31 5,52 4,96 4,56 4,25 4,01 3,82 3,66 3,52 3,41 3,31	6209 99,45 26,69 14,02 9,55 7,40 6,16 5,36 4,81 4,41 4,10 3,86 3,66 3,51 3,37 3,26 3,16	6261 99,47 26,50 13,84 9,38 7,23 5,99 5,20 4,65 4,25 3,94 3,70 3,51 3,35 3,21 3,10 3,00	6366 99,50 26,13 13,46 9,02 6,88 5,65 4,86 4,31 3,91 3,60 3,36 3,17 3,00 2,87 2,75 2,65

Окончание табл. 2

∞

18 19 20 21 24 25 26 27 28 29 30 40 60 120 ∞

8,29 8,18 8,10 8,02 7,82 7,77 7,72 7,68 7,64 7,60 7,56 7,31 7,08 6,85 6,63

6,01 5,93 5,85 5,78 5,61 5,57 5,53 5,49 5,45 5,42 5,39 5,18 4,98 4,79 4,61

5,09 5,01 4,94 4,87 4,72 4,68 4,64 4,60 4,57 4,54 4,51 4,31 4,13 3,95 3,78

4,58 4,50 4,43 4,37 4,22 4,18 4,14 4,11 4,07 4,04 4,02 3,85 3,63 3,48 3,32

4,25 4,17 4,10 4,04 3,90 3,85 3,82 3,78 3,75 3,73 3,70 3,51 3,34 3,17 3,02

4,01 3,94 3,87 3,81 3,67 3,63 3,59 3,56 3,53 3,50 3,47 3,29 3,12 2,96 2,80

3,84 3,77 3,70 3,64 3,50 3,46 3,42 3,39 3,36 3,33 3,30 3,12 2,95 2,79 2,64

3,71 3,61 3,56 3,51 3,36 3,32 3,29 3,26 3,23 3,20 3,17 2,99 2,82 2,66 2,51

3,60 3,52 3,46 3,40 326 3,22 3,18 3,15 3,12 3,09 3,07 2,89 2,72 2,56 2,41

3,51 3,43 3,37 3,31 3,17 3,13 3,09 3,06 3,03 3,00 2,98 2,80 2,63 2,47 2,32

3,37 3,30 3,23 3,17 3,03 2,99 2,96 2,93 2,90 2,87 2,84 2,66 2,50 2,34 2,18

3,23 3,15 3,09 3,03 2,89 2,85 2,81 2,78 2,75 2,73 2,70 2,52 2,35 2,19 2,04

3,08 3,00 2,94 2,88 2,74 2,70 2,66 2,63 2,60 2,57 2,55 2,37 2,20 2,03 1,88

2,92 2,84 2,78 2,72 2,58 2,54 2,50 2,47 2,44 2,41 2,39 2,20 2,03 1,86 1,70

2,57 2,49 2,42 2,36 2,21 2,17 2,13 2,10 2,06 2,03 2,01 1,80 1,60 1,38 1,00

Таблица 3

Значение G – критерия Кохрена

(f – число степеней свободы выборки; m – количество выборок)

m	f
m	1	2	3	4	5	6	7	8	9	10	16	36	144	∞
q = 0,05
2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120	0,99 0,97 0,91 0,84 0,78 0,73 0,68 0,64 0,60 0,54 0,47 0,39 0,34 0,29 0,24 0,17 0,10	0,98 0,87 0,77 0,68 0,62 0,56 0,52 0,48 0,45 0,39 0,33 0,27 0,24 0,20 0,16 0,11 0,06	0,94 0,80 0,68 0,60 0,53 0,48 0,44 0,40 0,27 0,33 0,28 0,22 0,19 0,16 0,13 0,09 0,05	0,91 0,75 0,63 0,54 0,48 0,43 0,39 0,36 0,33 0,29 0,24 0,19 0,17 0,14 0,11 0,09 0,04	0,88 0,71 0,59 0,51 0,44 0,40 0,36 0,33 0,30 0,26 0,22 0,17 0,15 0,12 0,10 0,07 0,04	0,85 0,68 0,56 0,48 0,42 0,37 0,34 0,31 0,28 0,24 0,20 0,16 0,14 0,11 0,09 0,06 0,03	0,83 0,65 0,54 0,46 0,40 0,35 0,32 0,29 0,27 0,23 0,19 0,15 0,13 0,11 0,08 0,06 0,03	0,82 0,63 0,52 0,44 0,38 0,34 0,30 0,28 0,25 0,22 0,18 0,14 0,12 0,10 0,08 0,06 0,03	0,80 0,62 0,50 0,42 0,37 0,33 0,29 0,27 0,24 0,21 0,17 0,14 0,12 0,10 0,07 0,05 0,03	0,79 0,60 0,49 0,41 0,36 0,32 0,28 0,26 0,24 0,20 0,17 0,13 0,11 0,09 0,07 0,05 0,03	0,73 0,55 0,44 0,36 0,31 0,28 0,25 0,22 0,20 0,17 0,14 0,11 0,09 0,08 0,06 0,04 0,02	0,66 0,47 0,37 0,31 0,26 0,23 0,20 0,18 0,17 0,14 0,11 0,09 0,07 0,06 0,05 0,03 0,02	0,58 0,40 0,31 0,25 0,21 0,18 0,16 0,14 0,13 0,11 0,09 0,07 0,06 0,05 0,03 0,02 0,01	0,50 0,33 0,25 0,20 0,17 0,14 0,13 0,11 0,10 0,08 0,07 0,05 0,04 0,03 0,03 0,02 0,01

Окончание табл.3

m	f
m	1	2	3	4	5	6	7	8	9	10	16	36	144	∞
q = 0,01
2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120	0,99 0,99 0,97 0,93 0,88 0,84 0,79 0,75 0,72 0,65 0,57 0,48 0,42 0,36 0,29 0,22 0,12	0,99 0,94 0,86 0,79 0,72 0,66 0,62 0,57 0,54 0,48 0,41 0,33 0,29 0,24 0,19 0,14 0,08	0,98 0,88 0,78 0,70 0,63 0,57 0,52 0,48 0,45 0,39 0,33 0,27 0,23 0,19 0,15 0,11 0,06	0,96 0,83 0,72 0,63 0,56 0,51 0,46 0,43 0,39 0,33 0,29 0,23 0,20 0,16 0,13 0,09 0,05	0,94 0,79 068 0,59 0,52 0,47 0,42 0,39 0,36 0,31 0,26 0,20 0,18 0,15 0,11 0,08 0,04	0,92 0,76 0,64 0,55 0,49 0,43 0,39 0,36 0,33 0,29 0,24 0,19 0,16 0,13 0,10 0,07 0,04	0,90 0,73 0,61 0,53 0,46 0,41 0,37 0,34 0,31 0,27 0,22 0,17 0,15 0,12 0,10 0,07 0,04	0,88 0,71 0,59 0,50 0,44 0,39 0,35 0,32 0,29 0,25 0,21 0,16 0,14 0,12 0,09 0,06 0,03	0,87 0,69 0,57 0,49 0,42 0,38 0,34 0,31 0,28 0,24 0,20 0,16 0,13 0,12 0,09 0,06 0,03	0,85 0,67 0,55 0,47 0,41 0,36 0,32 0,30 0,27 0,23 0,19 0,15 0,13 0,11 0,08 0,06 0,03	0,79 0,61 0,49 0,41 0,35 0,31 0,28 0,25 0,23 0,20 0,16 0,12 0,11 0,09 0,07 0,05 0,02	0,71 0,52 0,41 0,34 0,29 0,25 0,22 0,20 0,18 0,15 0,13 0,10 0,08 0,07 0,05 0,03 0,02	0,61 0,42 0,33 0,26 0,22 0,19 0,17 0,15 0,14 0,12 0,09 0,07 0,06 0,05 0,04 0,02 0,01	0,50 0,33 0,25 0,20 0,17 0,14 0,13 0,11 0,10 0,08 0,07 0,05 0,04 0,03 0,03 0,02 0,01

Таблица 4

Значения критерия 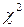( k – число степеней свободы)

00,5

0,01

0,05

0,01

0,05

0,01

0,05

0,01

1 2 3 4 5 6 7 8 9 10 11 12 13

3,84 5,99 7,81 9,49 11,1 12,6 14,1 15,5 16,9 18,3 19,7 21,0 22,4

6,63 9,21 11,3 13,3 15,1 16,8 18,5 20,1 21,7 23,2 24,7 26,2 27,7

14 15 16 17 18 19 20 21 22 23 24 25 26

23,7 25,0 26,3 27,6 28,9 30,1 31,4 32,7 33,9 35,2 36,4 37,7 38,9

29,1 30,6 32,0 33,4 34,8 36,2 37,6 38,9 40,3 41,6 43,0 44,3 45,6

27 28 29 30 31 32 33 34 35 36 37 38 39

40,1 41,3 42,6 43,8 45,0 46,2 47,4 48,6 49,8 51,0 52,2 53,4 54,6

47,0 48,3 49,6 50,9 52,2 53,2 54,8 56,1 57,3 58,6 59,9 61,2 62,4

40 41 42 43 44 45 46 47 48 49 50

55,8 56,9 58,1 59,3 60,5 61,7 62,8 64,0 65,2 66,3 67,5

63,7 65,0 66,2 67,5 68,7 70,0 71,2 72,4 73,7 74,9 76,2

Таблица 5

Равномерно распределенные случайные числа

10	09	73	25	33	76	52	01	35	86	34	67	35	48	76	80	95	90	91	17
37	54	20	48	05	64	89	47	42	96	24	80	52	40	37	20	63	61	04	02
08	42	26	89	53	19	64	50	93	03	23	20	90	25	60	15	95	33	47	64
99	01	90	25	29	09	37	67	07	15	38	31	13	11	65	88	67	67	43	97
12	80	79	99	70	80	15	73	61	47	64	03	23	66	53	98	95	11	68	77
66	06	57	47	17	34	07	27	68	50	36	69	73	61	70	65	81	33	98	85
31	06	01	08	05	45	57	18	24	06	35	30	34	26	14	86	79	90	74	39
85	26	97	76	02	02	05	16	56	92	68	66	57	48	18	73	05	38	52	47
63	57	33	21	35	05	32	54	70	48	90	55	35	75	48	28	46	82	87	09
73	79	64	57	53	03	52	96	47	78	35	80	83	42	82	60	93	52	03	44
98	52	01	77	67	14	90	56	86	07	22	10	94	05	58	60	97	09	34	33
11	80	50	54	31	39	80	82	77	32	50	72	56	82	48	29	40	52	42	01
83	45	29	96	34	06	28	89	80	83	13	74	67	00	78	18	47	54	06	10
88	68	54	02	00	86	50	75	84	01	36	76	66	79	51	90	36	47	64	93
99	59	46	73	48	87	51	76	49	69	91	82	60	89	28	93	78	56	13	68
65	48	11	76	74	17	46	85	09	50	58	04	77	69	74	73	03	95	71	86
80	12	43	56	35	17	72	70	80	15	45	31	82	23	74	21	11	57	82	53
74	35	09	98	17	77	40	27	72	14	43	23	60	02	10	45	52	16	42	37
69	91	62	68	03	66	25	22	91	48	36	93	68	72	03	76	62	11	39	90
09	89	32	05	05	14	22	56	85	14	46	42	75	67	88	96	29	77	88	22

СПИСОК ЛИТЕРАТУРЫ

1.Кане М. М. Исследования и изобретательство в машиностроении /И. Л. Барщай, Г. Я. Беляев, О. Г. Девойно// Под общ. ред. М. М. Кане.-Мн.: УП Технопринт, 2003.-237с, ISBN 985-464-479-0

2.Пижурин А. А., Пижурин А. А. Основы научных исследований в деревообработке. – М: МГУЛ, 2005.-ЗО6с.

З.Спиридонов А. А. Планирование эксперимента при исследовании технологических процессов.– М.: Машиностроение, 1981.- 184с., ББК 34.5 С72.

Учебное пособие

Гусев Владимир Григорьевич

Теория и практика планирования многофакторных экспериментов.

Учебное пособие по изучению курса для магистрантов и аспирантов

Редактор

Корректор

Компьютерная верстка

ЛР№…….. Подписано / печать……..

Формат 60*84/16. Бумага для множит. техники

Гарнитура Таймс

Печать на ризографе. Усл. Печ. Листов……Уч. – изд.л……Тираж……Заказ

Редакционно-издательский комплекс

Владимирского государственного университета.

600000, г. Владимир, ул. Горького, 87

Оглавление

Предисловие……………………………………………………………

1.Основные понятия и определения

1.1.Понятия и характеристика однофакторного, многофакторного

экспериментов, понятие планирования экспериментов…………………

1.2. Понятия объекта исследования, параметра оптимизации, фактора и требования, предъявляемые к ним………..…………………………………

2.Планирование и реализация полного факторного эксперимента

2.1.Выбор факторов и их кодирование……………………………………

2.2.Выбор модели……………………………………………………………

2.3.Полный факторный эксперимент………………………………………

2.4.Проведение опытов………………………………………………………

2.5.Крутое восхождение по поверхности отклика………...……………

2.6.Дробный факторный эксперимент………………………………...…

3. Планирование и реализация многофакторного эксперимента второго порядка

3.1.Центральные композиционные планы………………………...………

3.2.0ртогональные планы…………………………………………...………

3.3.Рототабельные планы……………………………………………..……

3.4.Исследование области оптимума, представленной полиномом второй степени…………………………………………………………………….

3.5.Исследование аэродинамических потоков, генерируемых дискретными шлифовальными кругами, на основе центрального композиционного планирования второго порядка……………………………

4.Применение планирования многофакторных экспериментов при механической обработке

4.1.Исследование шероховатости поверхности с использованием ротатабельного планирования…………………………………………….……..

4.2.0птимизация геометрии режущего инструмента на основе метода Бокса-Уилсона…………………………………………………………….……….

4.3.Применение ротатабельного планирования второго порядка для исследования процесса торцового фрезерования……………………………..

4.4.Составление композиционного плана проведения экспериментов при анализе параметров процесса шлифования………………………………

4.5.Исследование шероховатости поверхности, обработанной хонингованием…………………………………………………………………….

4.6.Исследование температуры, возникающей в процессе резания……

Приложение. Таблицы математической статистики…………………….

Список литературы………………………………………

Дата: 2018-12-28, просмотров: 288.

⇐ Предыдущая 2 3 4 5 6 7 8 9 1011

10	09	73	25	33	76	52	01	35	86	34	67	35	48	76	80	95	90	91	17
37	54	20	48	05	64	89	47	42	96	24	80	52	40	37	20	63	61	04	02
08	42	26	89	53	19	64	50	93	03	23	20	90	25	60	15	95	33	47	64
99	01	90	25	29	09	37	67	07	15	38	31	13	11	65	88	67	67	43	97
12	80	79	99	70	80	15	73	61	47	64	03	23	66	53	98	95	11	68	77
66	06	57	47	17	34	07	27	68	50	36	69	73	61	70	65	81	33	98	85
31	06	01	08	05	45	57	18	24	06	35	30	34	26	14	86	79	90	74	39
85	26	97	76	02	02	05	16	56	92	68	66	57	48	18	73	05	38	52	47
63	57	33	21	35	05	32	54	70	48	90	55	35	75	48	28	46	82	87	09
73	79	64	57	53	03	52	96	47	78	35	80	83	42	82	60	93	52	03	44
98	52	01	77	67	14	90	56	86	07	22	10	94	05	58	60	97	09	34	33
11	80	50	54	31	39	80	82	77	32	50	72	56	82	48	29	40	52	42	01
83	45	29	96	34	06	28	89	80	83	13	74	67	00	78	18	47	54	06	10
88	68	54	02	00	86	50	75	84	01	36	76	66	79	51	90	36	47	64	93
99	59	46	73	48	87	51	76	49	69	91	82	60	89	28	93	78	56	13	68
65	48	11	76	74	17	46	85	09	50	58	04	77	69	74	73	03	95	71	86
80	12	43	56	35	17	72	70	80	15	45	31	82	23	74	21	11	57	82	53
74	35	09	98	17	77	40	27	72	14	43	23	60	02	10	45	52	16	42	37
69	91	62	68	03	66	25	22	91	48	36	93	68	72	03	76	62	11	39	90
09	89	32	05	05	14	22	56	85	14	46	42	75	67	88	96	29	77	88	22

10	09	73	25	33	76	52	01	35	86	34	67	35	48	76	80	95	90	91	17
37	54	20	48	05	64	89	47	42	96	24	80	52	40	37	20	63	61	04	02
08	42	26	89	53	19	64	50	93	03	23	20	90	25	60	15	95	33	47	64
99	01	90	25	29	09	37	67	07	15	38	31	13	11	65	88	67	67	43	97
12	80	79	99	70	80	15	73	61	47	64	03	23	66	53	98	95	11	68	77
66	06	57	47	17	34	07	27	68	50	36	69	73	61	70	65	81	33	98	85
31	06	01	08	05	45	57	18	24	06	35	30	34	26	14	86	79	90	74	39
85	26	97	76	02	02	05	16	56	92	68	66	57	48	18	73	05	38	52	47
63	57	33	21	35	05	32	54	70	48	90	55	35	75	48	28	46	82	87	09
73	79	64	57	53	03	52	96	47	78	35	80	83	42	82	60	93	52	03	44
98	52	01	77	67	14	90	56	86	07	22	10	94	05	58	60	97	09	34	33
11	80	50	54	31	39	80	82	77	32	50	72	56	82	48	29	40	52	42	01
83	45	29	96	34	06	28	89	80	83	13	74	67	00	78	18	47	54	06	10
88	68	54	02	00	86	50	75	84	01	36	76	66	79	51	90	36	47	64	93
99	59	46	73	48	87	51	76	49	69	91	82	60	89	28	93	78	56	13	68
65	48	11	76	74	17	46	85	09	50	58	04	77	69	74	73	03	95	71	86
80	12	43	56	35	17	72	70	80	15	45	31	82	23	74	21	11	57	82	53
74	35	09	98	17	77	40	27	72	14	43	23	60	02	10	45	52	16	42	37
69	91	62	68	03	66	25	22	91	48	36	93	68	72	03	76	62	11	39	90
09	89	32	05	05	14	22	56	85	14	46	42	75	67	88	96	29	77	88	22

10	09	73	25	33	76	52	01	35	86	34	67	35	48	76	80	95	90	91	17
37	54	20	48	05	64	89	47	42	96	24	80	52	40	37	20	63	61	04	02
08	42	26	89	53	19	64	50	93	03	23	20	90	25	60	15	95	33	47	64
99	01	90	25	29	09	37	67	07	15	38	31	13	11	65	88	67	67	43	97
12	80	79	99	70	80	15	73	61	47	64	03	23	66	53	98	95	11	68	77
66	06	57	47	17	34	07	27	68	50	36	69	73	61	70	65	81	33	98	85
31	06	01	08	05	45	57	18	24	06	35	30	34	26	14	86	79	90	74	39
85	26	97	76	02	02	05	16	56	92	68	66	57	48	18	73	05	38	52	47
63	57	33	21	35	05	32	54	70	48	90	55	35	75	48	28	46	82	87	09
73	79	64	57	53	03	52	96	47	78	35	80	83	42	82	60	93	52	03	44
98	52	01	77	67	14	90	56	86	07	22	10	94	05	58	60	97	09	34	33
11	80	50	54	31	39	80	82	77	32	50	72	56	82	48	29	40	52	42	01
83	45	29	96	34	06	28	89	80	83	13	74	67	00	78	18	47	54	06	10
88	68	54	02	00	86	50	75	84	01	36	76	66	79	51	90	36	47	64	93
99	59	46	73	48	87	51	76	49	69	91	82	60	89	28	93	78	56	13	68
65	48	11	76	74	17	46	85	09	50	58	04	77	69	74	73	03	95	71	86
80	12	43	56	35	17	72	70	80	15	45	31	82	23	74	21	11	57	82	53
74	35	09	98	17	77	40	27	72	14	43	23	60	02	10	45	52	16	42	37
69	91	62	68	03	66	25	22	91	48	36	93	68	72	03	76	62	11	39	90
09	89	32	05	05	14	22	56	85	14	46	42	75	67	88	96	29	77	88	22