Для того, чтобы принять или забраковать гипотезу при помощи этих критериев, устанавливают уровни их значимости.
Уровень значимости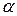 
представляет собой достаточно малое значение вероятности, отвечающее событиям, которые в данной обстановке исследования можно считать практически невозможными. Обычно принимают 5%-, 2%- или 1%-ный уровень значимости, в технике чаще всего принимают 5%-ный уровень.
Уровень значимости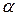 
называют также уровнем риска, который соответственно может быть принят равным 0,05, 0,02 или 0,01.
Так, например, при уровне значимости 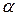= 0,05 вероятность при проверке нашей гипотезы Р = 1 – 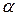=1– 0,05 = 0,95 или 95%. Это значит, что в среднем только в 5% случаев возможна ошибка при проверке гипотезы.
После вычисления по формуле (2.12) дисперсий опытов проверяют гипотезу однородности. Проверка однородности двух дисперсий производится с помощью F – критерия, который называется критерием Фишера и представляет собой отношение большей дисперсии к меньшей:
,
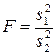где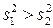 
.
Если расчетное значение Fp-критерия меньше табличного Ft (табл. 2.6) для соответствующих чисел степеней свободы и принятого уровня значимости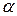 
, то дисперсии однородны.
Однородность ряда дисперсий проверяют по критерию Кохрена или критерию Бартлета.
При равномерном дублировании опытов однородность ряда дисперсий проверяют с помощью G-критерия Кохрена, представляющего собой отношение максимальной дисперсии к сумме всех дисперсий:
.
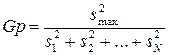Дисперсии однородны, если расчетное значение Gp - критерия не превышает табличного значения GT-критерия.
Индекс N показывает число сравниваемых дисперсий, а п - число параллельных опытов.
Если Gp>GT, то дисперсии неоднородны, а это указывает на то, что исследуемая величина у не подчиняется нормальному закону.
В этом случае нужно попытаться заменить y случайной величиной q = f ( y ), достаточно близкой к нормальному закону.
Если дисперсии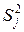 
опытов однородны, то дисперсию 
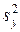воспроизводимости эксперимента вычисляют по выражению:
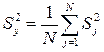, (2.14)
где N – число опытов или число строк матрицы планирования.
По результатам эксперимента вычисляют коэффициенты регрессии. Свободный член b 0 определяют по формуле:
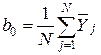. (2.15)
Таблица 2.6
Значения F-критерия (Фишера) при 5% - уровне значимости
| Число степеней свободы для меньшей дисперсии | Значения критерия при числе степеней свободы для большей дисперсии | ||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 12 | 24 | 
| |||||
| 1 | 164,4 | 199,5 | 215,7 | 224,6 | 230,2 | 234,0 | 244,9 | 249,0 | 254,3 | ||||
| 2 | 18,5 | 19,2 | 19,2 | 19,3 | 19,3 | 19,3 | 19,4 | 19,4 | 19,5 | ||||
| 3 | 10,1 | 9,6 | 9,3 | 9,1 | 9,0 | 8,9 | 8,7 | 8,6 | 8,5 | ||||
| 4 | 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | 6,2 | 5,9 | 5,8 | 5,6 | ||||
| 5 | 6,6 | 5,8 | 5,4 | 5,2 | 5,1 | 5,0 | 4,7 | 4,5 | 4,4 | ||||
| 6 | 6,0 | 5,1 | 4,8 | 4,5 | 4,4 | 4,3 | 4,0 | 3,8 | 3,7 | ||||
| 7 | 5,5 | 4,7 | 4,4 | 4,1 | 4,0 | 3,9 | 3,6 | 3,4 | 3,2 | ||||
| 8 | 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | 3,6 | 3,3 | 3,1 | 2,9 | ||||
| 9 | 5,1 | 4,3 | 3,9 | 3,6 | 3,5 | 3,4 | 3,1 | 2,9 | 2,7 | ||||
| 10 | 5,0 | 4,1 | 3,7 | 3,5 | 3,3 | 3,2 | 2,9 | 2,7 | 2,5 | ||||
| 11 | 4,8 | 4,0 | 3,6 | 3,4 | 3,2 | 3,1 | 2,8 | 2,6 | 2,4 | ||||
| 12 | 4,8 | 3,9 | 3,5 | 3,3 | 3,1 | 3,0 | 2,7 | 2,5 | 2,3 | ||||
| 13 | 4,7 | 3,8 | 3,4 | 3,2 | 3,0 | 2,9 | 2,6 | 2,4 | 2,2 | ||||
| 14 | 4,6 | 3,7 | 3,3 | 3,1 | 3,0 | 2,9 | 2,5 | 2,3 | 2,1 | ||||
| 15 | 4,5 | 3,7 | 3,3 | 3,1 | 2,9 | 2,8 | 2,5 | 2,3 | 2,1 | ||||
| 16 | 4,5 | 3,6 | 3,2 | 3,0 | 2,9 | 2,7 | 2,4 | 2,2 | 2,0 | ||||
| 17 | 4,5 | 3,6 | 3,2 | 3,0 | 2,8 | 2,7 | 2,4 | 2,2 | 2,0 | ||||
| 18 | 4,4 | 3,6 | 3,2 | 2,9 | 2,8 | 2,7 | 2,3 | 2,1 | 1,9 | ||||
| 19 | 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | 1,9 | ||||
| 20 | 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,3 | 2,1 | 1,8 | ||||
| 22 | 4,3 | 3,4 | 3,1 | 2,8 | 2,7 | 2,6 | 2,2 | 2,0 | 1,8 | ||||
| 24 | 4,3 | 3,4 | 3,0 | 2,8 | 2,6 | 2,5 | 2,2 | 2,0 | 1,7 | ||||
| 26 | 4,2 | 3,4 | 3,0 | 2,7 | 2,6 | 2,5 | 2,2 | 2,0 | 1,7 | ||||
| 28 | 4,2 | 3,3 | 3,0 | 2,7 | 2,6 | 2,4 | 2,1 | 1,9 | 1,7 | ||||
| 30 | 4,2 | 3,3 | 2,9 | 2,7 | 2,5 | 2,4 | 2,1 | 1,9 | 1,6 | ||||
| 40 | 4,1 | 3,2 | 2,9 | 2,6 | 2,5 | 2,3 | 2,0 | 1,8 | 1,5 | ||||
| 60 | 4,0 | 3,2 | 2,8 | 2,5 | 2,4 | 2,3 | 1,9 | 1,7 | 1,4 | ||||
| 120 | 3,9 | 3,1 | 2,7 | 2,5 | 2,3 | 2,2 | 1,8 | 1,6 | 1,3 | ||||
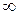
| 3,8 | 3,0 | 2,6 | 2,4 | 2,2 | 2,1 | 1,8 | 1,5 | 1,0 | ||||
Таблица 2.7
Значения G - критерия (Кохрена) при 5% – уровне значимости
| N | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 0,9065 | 0,7679 | 0,6841 | 0,6287 | 0,5895 | 0,5598 | 0,5365 | 0,5175 | 0,5017 |
| 6 | 0,7808 | 0,6161 | 0,5321 | 0,4803 | 0,4447 | 0,4184 | 0,3980 | 0,3817 | 0,3682 |
| 8 | 0,6798 | 0,5157 | 0,4377 | 0,3910 | 0,3595 | 0,3362 | 0,3185 | 0,3043 | 0,2926 |
| 10 | 0,6020 | 0,4450 | 0,3733 | 0,3311 | 0,3029 | 0,2823 | 0,2666 | 0,2541 | 0,2439 |
| 12 | 0,5410 | 0,3924 | 0,3624 | 0,2880 | 0,2624 | 0,2439 | 0,2299 | 0,2187 | 0,2098 |
| 15 | 0,4709 | 0,3346 | 0,2758 | 0,2419 | 0,2195 | 0,2034 | 0,1911 | 0,1815 | 0,1736 |
| 20 | 0,3894 | 0,2705 | 0,2205 | 0,1921 | 0,1735 | 0,1602 | 0,1501 | 0,1422 | 0.1357 |
Коэффициенты регрессии, характеризующие линейные эффекты, определяют по выражению
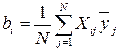. (2.16)
Коэффициенты регрессии, характеризующие эффекты взаимодействия, определяют по формуле
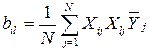, (2.17)
где i, l – номера факторов; Xij, Xlj – кодированные значения факторов i и l в j-м опыте.
Вычислив коэффициенты регрессии, проверяют их значимость.
Проверку значимости коэффициентов можно проводить двумя способами: 1) сравнением абсолютной величины коэффициентов с доверительным интервалом; 2) с помощью t-критерия, который называется критерием Стьюдента.
При проверке значимости коэффициентов первым способом для определения доверительного интервала вычисляют дисперсии коэффициентов регрессии. Доверительный интервал находится по формуле. Дисперсию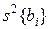 
i-гo коэффициента определяют по выражению
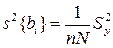. (2.18)
Доверительный интервал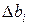 
находится по формуле
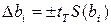, (2.19)
где t Т табличное значение критерия Стьюдента при принятом уровне значимости 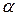и числе степеней свободы f, с которым определялась дисперсия воспроизводимости 
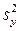. При равномерном дублировании опытов число степеней свободы находится по выражению f= (n – 1 )N, где N – число опытов в матрице планирования, a n – число параллельных опытов; 
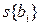– ошибка в определении i-го коэффициента регрессии вычисляемая по формуле 
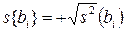. Значения t-критерия приведены в табл. 2.8.
Таблица 2.8.
Значения t-критерия при 5%-ном уровне значимости
| Число степеней свободы | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| Значения t-критерия | 12,71 | 4,30 | 3,18 | 2,78 | 2,57 | 2,45 | 2,37 | 2,30 |
| Число степеней свободы | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| Значения t-критерия | 2,26 | 2,23 | 2,20 | 2,18 | 2,16 | 2,14 | 2,13 | 2,12 |
| Число степеней свободы | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Значения t-критерия | 2,11 | 2,10 | 2,09 | 2,09 | 2,08 | 2,07 | 2,07 | 2,06 |
| Число степеней свободы | 25 | 26 | 27 | 28 | 29 | 30 | 40 | 60 |
| Значения t-критерия | 2,06 | 2,06 | 2,05 | 2,05 | 2,05 | 2,04 | 2,02 | 2,00 |
Коэффициент значим, если его абсолютная величина больше доверительного интервала.
При проверке значимости коэффициентов регрессии вторым способом вычисляют tp - критерий по выражению
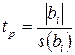(2.20)
и сравнивают его с табличным tT.
Коэффициент значим, если tp>tT для принятого уровня значимости 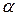и числа степеней свободы f, с которым определялась дисперсия 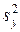. Критерий Стьюдента вычисляют для каждого коэффициента регрессии. Статистически незначимые коэффициенты могут быть исключены из уравнения.
После расчета коэффициентов регрессии и проверки их значимости определяют дисперсию адекватности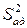 
.
Остаточная дисперсия, или дисперсия адекватности, характеризует рассеяние эмпирических значений параметра оптимизации относительно расчетных его значений, определенных по найденному уравнению регрессии. Дисперсию адекватности определяют по формуле
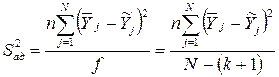(2.21)
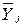– среднее арифметическое значение параметра оптимизации в j-м
опыте;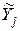 
– значение параметра оптимизации, вычисленное по модели для условий j-гo опыта; 
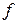– число степеней свободы, равное 
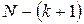; k – число факторов.
Последним этапом обработки результатов эксперимента является проверка гипотезы адекватности найденной модели. Проверку этой гипотезы производят по F-критерию (Фишера):
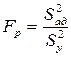. (2.22)
Если значение FP<FT для принятого уровня значимости и соответствующих чисел степеней свободы, то модель считают адекватной. При FP>FT гипотеза адекватности отвергается.
Таким образом, обработка результатов эксперимента при равномерном дублировании опытов следующая:
- для каждой строки матрицы планирования по формуле (2.11) вычисляют среднее арифметическое значение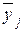 
параметра оптимизации;
- по формуле (2.12) определяют дисперсию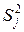 
каждого опыта матрицы планирования;
- используя критерий Кохрена, проверяют гипотезу однородности дисперсий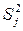 
опытов;
- если дисперсии опытов однородны, то по формуле (2.14) вычисляют дисперсию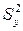 
воспроизводимости эксперимента;
- по формулам (2.15), (2.16), (2.17) определяют коэффициенты уравнения регрессии;
- по выражению (2.18) находят дисперсии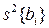 
коэффициентов регрессии;
- по формуле (2.19) устанавливают величину доверительного интервала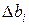 
;
- проверяют статистическую значимость коэффициентов регрессии;
- по выражению (2.21) определяют дисперсию адекватности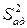 
;
- с помощью F-критерия проверяют гипотезу адекватности модели.
В заключение необходимо отметить, что использование критерия Кохрена, Стьюдента и Фишера предполагает нормальное распределение результатов эксперимента.
Обработка результатов эксперимента при неравномерном дублировании опытов, вследствие ошибок и необходимости их исключения отличается от рассмотренной обработки результатов. Количество параллельных опытов в каждой строке матрицы оказывается не одинаковым.
Бывают и другие случаи, когда по тем или иным причинам не удается провести одинаковое число параллельных опытов в каждом опыте. При неодинаковых числах параллельных опытов нарушается ортогональность
матрицы планирования и, как следствие, изменяются формулы для определения коэффициентов регрессии и их ошибок. Расчет коэффициентов регрессии и их ошибок при неодинаковых числах параллельных опытов усложняется.
Обработка результатов эксперимента при неравномерном дублировании опытов производится по следующей схеме [3]:
1. Для каждой строки матрицы планирования находят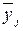 
– среднее арифметическое значение параметра оптимизации
,
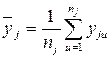где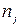 
–. число параллельных опытов в j-ой строке матрицы.
2. Для каждой строки матрицы вычисляют дисперсию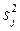 
опыта:
.
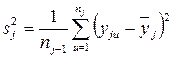3. Проверяют с помощью критерия Бартлета гипотезу однородности дисперсий опытов. Для этого подсчитывают дисперсию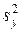 
воспроизводимости эксперимента по формуле
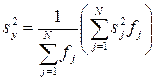, (2.23)
где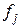 
– число степеней свободы, с которым определялась дисперсия 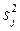j-го опыта.
После этого определяют величину
,
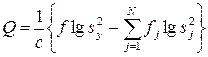где
; 
.
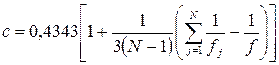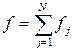Бартлет показал, что величина Q приближенно подчиняется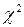 
распределению с (N–1) степенями свободы, где N – число сравниваемых дисперсий.
Если Q меньше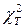 
(табл. 2.9) для данного числа (N–1) степеней свободы и принятого уровня значимости, то дисперсии однородны, и наоборот. Критерий Бартлета основан на нормальном распределении. Если распределение случайной величины не подчиняется нормальному закону, то проверка однородности дисперсий может привести к ошибочным результатам.
Рассмотрим применение критерия. Бартлета для проверки однородности дисперсий. Матрица планирования предусматривала выполнение четырех опытов. Первый опыт был повторен пять раз, второй – шесть, третий и четвертый – по четыре раза. При этом дисперсия первого опыта равна 3,5; второго – 4,22; третьего – 5,88; четвертого – 11,36. Необходимо проверить, верна ли гипотеза об однородности дисперсий.
Таблица 2.9
Значения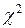 
при 5%- ном уровне значимости
| Число степеней свободы | Значения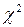 
| Число степеней свободы | Значения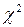
|
| 1 | 3,84 | 16 | 26,3 |
| 2 | 5,99 | 17 | 27,6 |
| 3 | 7,82 | 18 | 28,9 |
| 4 | 9,49 | 19 | 30,1 |
| 5 | 11,07 | 20 | 31,4 |
| 6 | 12,59 | 21 | 32,7 |
| 7 | 14,07 | 22 | 33,9 |
| 8 | 15,51 | 23 | 35,2 |
| 9 | 16,92 | 24 | 36,4 |
| 10 | 18,31 | 25 | 37,7 |
| 11 | 19,68 | 26 | 38,9 |
| 12 | 21,0 | 27 | 40,1 |
| 13 | 22,4 | 28 | 41,3 |
| 14 | 23,7 | 29 | 42,6 |
| 15 | 25,0 | 30 | 43,8 |
Дисперсия 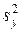параметра оптимизации
.
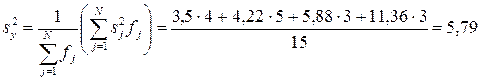Вычисляем величину с:
.
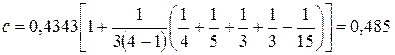Определяем Q: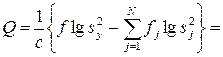 
.
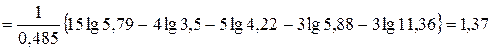Табличное значение 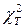для трех степеней свободы (N–1=3) и 5%-го уровня значимости равно 7,82.
Так как Q<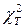 
, то гипотеза однородности дисперсий принимается.
4. Вычисляют коэффициенты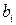 
уравнения регрессии, дисперсии 
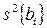коэффициентов регрессии и ошибки 
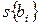в определении коэффициентов.
5. Для каждого коэффициента регрессии находят расчетное значение t-критерия
.
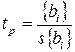Сравнивают расчетное значение tp с табличным значением tT-критерия. Табличное значение критерия находят для принятого уровня значимости и числа степеней свободы f, которое в рассматриваемом случае определяют по выражению
.
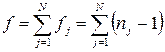Коэффициент значим при tp>tT и незначим при tp<tT. Статистически незначимые коэффициенты могут быть исключены из уравнения регрессии.
При исключении статистически незначимых коэффициентов из уравнения оставшиеся коэффициенты пересчитывают с использованием метода наименьших квадратов.
6. Определяют дисперсию адекватности
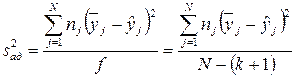, (2.24)
где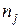 
– число параллельных опытов в j-й строке матрицы.
7. Проверяют гипотезу адекватности получений модели с помощью F-критерия. Если FP<FT для принятого уровня значимости и соответствующих чисел степеней свободы, то модель считают адекватной. При FP>FT гипотеза адекватности отвергается.
При отсутствии дублирования опытов обработку результатов эксперимента производят по следующей схеме:
1. Для вычисления дисперсии 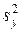воспроизводимости эксперимента выполняют несколько параллельных опытов в нулевой точке (в центре плана).
При постановке опытов в нулевой точке все факторы находятся на нулевых уровнях. По результатам опытов в центре плана вычисляют дисперсию 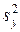воспроизводимости эксперимента
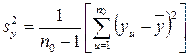, (2.25)
где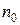 
– число параллельных опытов в нулевой точке; 
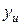– значение параметра оптимизации в u-м опыте; 
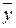– среднее арифметическое значение параметра оптимизации в 
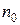параллельных опытах.
2. Закончив эксперимент, вычисляют коэффициенты регрессии. Свободный член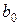 
определяют по формуле
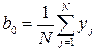. (2.26)
Коэффициенты регрессии, характеризующие линейные эффекты, вычисляют по выражению
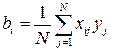. (2.27)
Коэффициенты регрессии, характеризующие эффекты взаимодействия, определяют по формуле
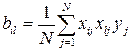, (2.28)
где i, l – номера факторов; j – номер строки или опыта в матрице планирования;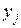 
– значение параметра оптимизации в j-м опыте; 
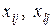– кодированные значения (±1) факторов i и l в j-м опыте.
3. Проверяют статистическую значимость коэффициентов уравнения регрессии. Проверку значимости коэффициентов можно производить двумя способами:
1) сравнением абсолютной величины коэффициента с доверительным интервалом;
2) с помощью t-критерия.
При проверке значимости коэффициентов первым способом для определения доверительного интервала вычисляют дисперсии коэффициентов регрессии по выражению
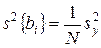, (2.29)
где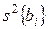 
– дисперсия i-го коэффициента регрессии; N – число строк или опытов в матрице планирования.
Из формулы (2.29) следует, что дисперсии всех коэффициентов равны. Доверительный интервал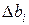 
определяют по формуле (2.19). Значение t-критерия, входящего в эту формулу, находят по таблице для принятого уровня значимости и числа степеней свободы f, которое определяют по выражению
f = n 0 –1.
Коэффициент регрессии значим, если его абсолютная величина больше доверительного интервала.
При проверке значимости коэффициентов вторым способом вычисляют критерий tp
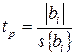
и сравнивают его с табличным tT. Коэффициент значим, если tp>tT для принятого уровня значимости и числа степеней свободы, определенного по формуле
f = n 0 –1.
Критерий Стьюдента t вычисляют для каждого коэффициента регрессии. Статистически незначимые коэффициенты регрессии могут быть исключены из уравнения.
4. Определяют дисперсию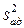 
адекватности по формуле
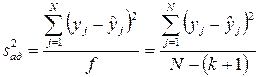, (2.30)
где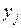 
– наблюденное значение параметра оптимизации в j-м опыте;
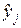– значение параметра оптимизации, вычисленное по модели для условий j-гo опыта;
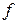– число степеней свободы, которое для линейной модели определяется по выражению 
,
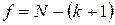где k – число факторов.
5. Проверяют гипотезу адекватности модели по F-критерию, используя для определения Fp-критерия формулу (2.22).
Если FP<FT для принятого уровня значимости и соответствующих чисел степеней свободы, то модель считают адекватной. При FP>FT гипотеза адекватности отвергается. В этом случае для получения адекватной модели принимают одно из следующих решений:
1) переходят к планированию второго или более высокого порядка;
2) уменьшают интервалы варьирования и ставят новый эксперимент, повторяя эти действия до получения адекватной линейной модели.
Если линейная модель адекватна, то переходят к методу крутого восхождения.
Необходимо заметить, что крутое восхождение эффективно тогда, когда все коэффициенты при факторах значимы.
Незначимость некоторых коэффициентов может получиться вследствие неудачно выбранных интервалов варьирования; включения факторов, не влияющих на параметр оптимизации; большой ошибки опыта.
Принятие решения в данной ситуации зависит от того, какая из трех гипотез выбрана. Если принята первая гипотеза, то изменяют интервалы варьирования по незначимым факторам и ставят новую серию опытов.
Если принята вторая, то не влияющие факторы стабилизируют и исключают из опытов.
Если принята третья гипотеза, то увеличивают число параллельных опытов. Увеличение числа – этих опытов приводит к уменьшению дисперсии коэффициентов и величины доверительного интервала, в результате все или часть коэффициентов могут оказаться значимыми.
Возможен случай, когда все коэффициенты, кроме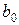 
, незначимы, а модель адекватна. Такая ситуация чаще всего возникает из-за слишком узких интервалов варьирования или вследствие большой ошибки опыта. В этой ситуации возможны два решения:
1) расширение интервалов варьирования или
2) повышение точности эксперимента путем улучшения методики проведения опытов и увеличения числа параллельных опытов.
Дата: 2018-12-28, просмотров: 384.
