В качестве факторов рекомендуется выбирать такие независимые переменные величины, которые оказывают наибольшее влияние на параметры оптимизации и отвечают выше сформулированным требованиям. На начальной стадии исследований экспериментатор не знает, какие независимые переменные, подаваемые на вход того или иного процесса, в наибольшей степени влияют на его протекание. Поэтому ему следует воспользоваться априорной информацией, содержащейся в научно-технической, справочной литературе, диссертациях и других публикациях предшественников. Если в указанных источниках такой информации не существует, то возможен опрос ученых и специалистов, работающих в данной области.

В случае исследования принципиально нового, ранее неизвестного процесса, явления или устройства при отсутствии какой-либо априорной информации экспериментатору следует прибегнуть к проведению предварительных однофакторных экспериментов, целью которых является выявление доминирующих факторов процесса и характера зависимости, связывающей тот или иной фактор с тем или иным параметром процесса.

После обоснованного выбора параметров оптимизации и факторов устанавливают уровни и интервалы варьирования факторов, при этом необходимо определить какие пределы изменения факторов допускает экспериментальная установка, какой характер изменения факторов возможен (дискретный или непрерывный). Верхний и нижний уровни необходимо устанавливать таким образом, чтобы оставался запас варьирования фактора для возможного расширения (увеличения и уменьшения) факторного пространства при необходимости проведения серии дополнительных опытов в случае неадекватности модели, полученной на первой стадии экспериментальных исследований.

Оперирование абсолютными значениями факторов усложняет статистическую обработку результатов многофакторных экспериментов, поэтому для упрощения этой процедуры факторы необходимо закодировать. В кодированном виде верхний уровень обозначают +1, нижний – 1, а основной – 0.

Натуральное значение фактора – это численное значение фактора в абсолютных единицах измерения (например, скорость подачи S режущего инструмента, измеряемая в мм/об; глубина резания t, измеряемая в мм и т.д.). Натуральное значение факторов необходимо закодировать, при этом оперирование с кодовыми обозначениями факторов упрощает вычисления при обработке экспериментальных данных. Факторы кодируют в соответствии с формулой

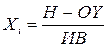,                                                                                                      (2.2)

где Н – натуральное значение фактора; ОУ – основной уровень фактора; ИВ – интервал варьирования фактора

Пример 1.

Требуется закодировать абсолютные численные значения скорости подачи режущего инструмента S, если верхний уровень этого фактора ВУ=1,5мм/об, а нижний уровень НУ=0,5мм/об.

Находим основной уровень (ОУ) фактора и интервал варьирования (ИВ) в абсолютном выражении

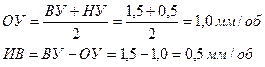.                                                               (2.3)

Подставляем в выражение (2.2) численные значения основного уровня (ОУ) и интервала варьирования (ИВ) фактора «скорость подачи», определяемые по выражению (2.3), при этом одновременно заменяем обозначение натурального значения Н на конкретное обозначение скорости подачи S. В результате получим выражение для кодирования первого фактора S(X ₁)

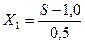.                                                                                                            (2.4)

Подставляя поочередно в выражение (2.4) вместо S численные значения верхнего, нижнего и основного уровней, получим кодовые значения скорости подачи для названных уровней

.

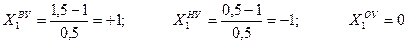Пример 2.

Требуется закодировать абсолютные численные значения глубины резания t , если верхний уровень этого фактора ВУ = 3,5мм, а нижний уровень НУ = 0,5мм.

Поступая аналогично первому примеру, получим:

.

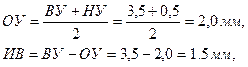
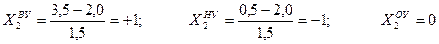На основании изложенной методики выполняют не только кодирование факторов, но и перевод уравнения регрессии с кодовыми обозначениями факторов к уравнению регрессии, содержащему натуральные значения факторов.

Выбор модели

Перед проведением опытов, экспериментатор должен выбрать вид уравнения регрессии (модели). Выбор модели – это сложный процесс, связанный со многими обстоятельствами и соображениями. Как отмечалось выше, под математической моделью будем понимать функцию отклика. Выбрать модель – это значит выбрать вид этой функции, записать её уравнение. Затем спланировать и поставить эксперимент для отыскания численных значений коэффициентов уравнения.

Моделей бывает много и разных. Чтобы выбрать одну из них, надо четко знать, что мы хотим от модели, какие требования к ней предъявляем.

Исходя из выбранной стратегии, ясно, что главное требование к модели – это способность предсказывать направление дальнейших опытов с требуемой точностью. Так как до получения модели не известно, какое направление нам понадобится, то естественно требовать, чтобы точность предсказания во всех возможных направлениях была бы одинакова. Это значит, что в некоторой подобласти, в которую входят выполненные опыты, предсказанное с помощью модели значение отклика не должно отличаться больше, чем на некоторую заранее заданную величину. Модель, удовлетворяющая такому условию, называется адекватной. Если несколько различных моделей отвечает нужным требованиям, то следует выбрать ту из них, которая является самой простой. Модель выбирают на основании априорной информации либо на основании результатов предварительных экспериментов. Для двух факторов могут быть выбраны следующие виды моделей.

модель первой степени

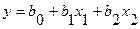,                                                                                   (2.5)

модель второй степени

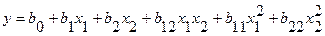,                                               (2.6)

модель третьей степени

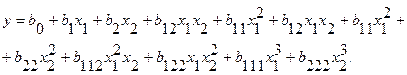                             (2.7)

Выражения (2.5) – (2.7) называются уравнениями регрессии, а коэффициенты, стоящие перед кодовыми значениями факторов – коэффициентами регрессии. Итак, мы представили неизвестную нам функцию полиномом. Замена одной функции другой, примерно эквивалентной функцией, называется аппроксимацией. Следовательно, мы аппроксимировали неизвестную нам функцию полиномом. Но, как показано на примере, полиномы бывают различных степеней. Какой полином взять на первом шаге?

Эксперимент нужен для расчета численных значений коэффициентов регрессии. Поэтому, чем больше коэффициентов, тем больше опытов нужно поставить. Мы же стремимся сократить их число. Следовательно, надо найти полином, содержащий как можно меньше коэффициентов, но удовлетворяющий требованиям, предъявляемым к модели. При заданном числе факторов, чем ниже степень полинома, тем меньше в нем коэффициентов.

С другой стороны, нужно, чтобы модель предсказывала направление наискорейшего улучшения параметра оптимизации. Такое направление называют направлением градиента. Движение в этом направлении приведет к успеху быстрее, чем движение в любом другом направлении. В этом случае лучше использовать полином первой степени, так как он содержит информацию о направлении градиента, и, кроме того, в нем минимально возможное число коэффициентов при данном числе факторов.

Единственное опасение в том, будет ли линейная модель всегда адекватной. Однако всегда существует такая окрестность любой (почти любой) точки, в которой линейная модель адекватна. Размер такой области заранее не известен, но адекватность можно проверять по результатам эксперимента. Следовательно, выбрав сначала произвольную подобласть, мы рано или поздно найдем ее требуемые размеры. Как только это случится, воспользуемся движением по градиенту. Затем ищем линейную модель в другой подобласти. Цикл повторяется до тех пор, пока движение по градиенту не перестанет давать эффект. Это значит, что мы попали в область, близкую к оптимуму. Такая область называется «почти стационарной». Здесь линейная модель уже не нужна. Чтобы подробнее описать область оптимума, нужно перейти к полиномам более высокой степени.

Кроме задачи оптимизации, может возникать задача математического описания объекта исследования - построения интерполяционной модели. В этом случае нас не интересует оптимум. Здесь нам нужно предсказать результат с требуемой точностью во всех точках некоторой заранее заданной области. С этой целью последовательно увеличивают степень полинома до тех пор, пока модель не окажется адекватной.

Таким образом, на первой стадии экспериментальных исследований при отсутствии сведений о модели разумно выбирать модель первого порядка. Если же есть сведения о нелинейности, то принимается модель второго порядка.

Задачей планирования многофакторных экспериментов является отыскание коэффициентов регрессии, после чего модель процесса или модель функционирования устройства становится известной.