При большом числе факторов (k>3) проведение полного факторного эксперимента связано с большим числом опытов, значительно превосходящим число коэффициентов линейной модели. Если при получении модели можно ограничиться линейным приближением, т. е. получить адекватную модель в виде полинома 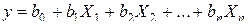 , то число опытов можно резко сократить в результате применения дробного факторного эксперимента.
, то число опытов можно резко сократить в результате применения дробного факторного эксперимента.
Так, например, в полном факторном эксперименте типа 22 при линейном приближении коэффициент регрессии b 12 можно принять равным нулю, а столбец X 1 Х2 матрицы использовать для третьего фактора Х3.
В этом случае линейная модель будет выражаться уравнением 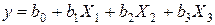 . Для определения коэффициентов этого уравнения достаточно провести четыре опыта вместо восьми в полном факторном эксперименте типа 23.
. Для определения коэффициентов этого уравнения достаточно провести четыре опыта вместо восьми в полном факторном эксперименте типа 23.
План эксперимента, предусматривающий реализацию половины опытов полного факторного эксперимента, называют полурепликой.
При увеличении числа факторов (k>3) возможно применение реплик большей дробности.
Дробной репликой называют план эксперимента, являющийся частью плана полного факторного эксперимента.
Дробные реплики обозначают выражением 2 k -р , где р – число линейных эффектов, приравненных к эффектам взаимодействия. При р = 1 получают полуреплику; при р = 2 получают 1/4 – реплику; при р = 3 получают 1/8 – реплику и т. д. по степеням двойки. Так, например, если в полном факторном эксперименте 23 (табл. 2.15) один из эффектов взаимодействия (Х1Х2, Х1ХЗ, Х2ХЗ, Х1Х2ХЗ) заменим четвертым фактором Х4 то получим полуреплику 24-1 от полно го факторного эксперимента 24.
Если два эффекта взаимодействия заменить факторами Х4 и Х5, то получим 1/4 – реплику 25-2 от полного факторного эксперимента 25. Можно получить 1/8 – реплику от полного факторного эксперимента, заменив три эффекта взаимодействия факторами Х4, Х5 и Х6.
Таблица 2.15
Матрица полного факторного эксперимента типа 23
| Номер опыта | X 0 | X 1 | Х2 | Х3 | X 1 Х2 | X 1 Х3 | X 2 Х3 | X 1 Х2 Х3 | Yi |
| 1 | + | – | – | + | + | – | – | + | Y 1 |
| 2 | + | + | – | + | – | + | – | – | Y2 |
| 3 | + | – | + | + | – | – | + | – | Y3 |
| 4 | + | + | + | + | + | + | + | + | Y4 |
| 5 | + | – | – | – | + | + | + | – | Y 5 |
| 6 | + | + | – | – | – | – | + | + | Y 6 |
| 7 | + | – | + | – | – | + | – | + | Y 7 |
| 8 | + | + | + | – | + | – | – | – | Y 8 |
Если заменить четыре эффекта взаимодействия факторами Х4, Х5 и Х6 и Х7, то получим 1/16 – реплику 27-4 от полного факторного эксперимента 27. Реплики, которые используют для сокращения числа опытов в 2m раз, где т = 1, 2, 3, ..., называют регулярными. В связи с тем, что в дробных репликах часть взаимодействий заменена новыми факторами, найденные коэффициенты уравнения регрессии будут являться совместными оценками линейных эффектов и эффектов взаимодействия. Коэффициенты 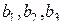 будут оценками совмещенных эффектов, а именно
будут оценками совмещенных эффектов, а именно
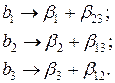
Коэффициент b 1 является оценкой влияния фактора X 1 и парного взаимодействия X 2 X 3 на функцию отклика. Влияние фактора X 1 в этом случае характеризуется величиной 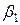 , а влияние взаимодействия – величиной
, а влияние взаимодействия – величиной 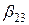 . Оценки, в которых невозможно разделить линейный эффект и эффект взаимодействия, называют смешанными. Линейные эффекты рекомендуется смешивать, прежде всего, с их взаимодействиями, которые согласно априорной информации незначимы.
. Оценки, в которых невозможно разделить линейный эффект и эффект взаимодействия, называют смешанными. Линейные эффекты рекомендуется смешивать, прежде всего, с их взаимодействиями, которые согласно априорной информации незначимы.
Число смешанных линейных эффектов в дробной реплике называют ее разрешающей способностью[2]. Часто приходится решать задачи, в которых заранее можно полагать, что эффекты взаимодействия, хотя и малы по сравнению с линейными, но все же не равны нулю. В таких случаях необходимо заранее определить, какие коэффициенты являются смешанными оценками. Тогда в зависимости от условий поставленной задачи, подбирается такая дробная реплика, с помощью которой можно извлечь максимальную информацию из эксперимента. Прямая оценка разрешающей способности дробной реплики затруднена. Поэтому дробные реплики задают с помощью генерирующих соотношений. Генерирующим называют соотношение, которое показывает, какое из взаимодействий принято незначимым и заменено новым фактором. План типа 23-1 может быть представлен двумя полурепликами (табл. 3), которые задаются одним из следующих генерирующих соотношений:
 . (2.32)
. (2.32)
Генерирующие соотношения умножим на новую независимую переменную х3:
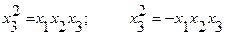 . (2.33)
. (2.33)
Таблица 2.16
Две полуреплики 23-1
| Номер опыта | X 3 = X 1 X 2 | Номер опыта | X 3 = – X 1 X 2 | ||||
| X 1 | X 2 | Х3 | X 1 | X 2 | Х3 | ||
| 1 | – | + | – | 1 | – | + | + |
| 2 | + | + | + | 2 | + | + | – |
| 3 | – | – | + | 3 | – | – | – |
| 4 | + | – | – | 4 | + | – | + |
Поскольку всегда 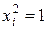 , то получим следующие выражения:
, то получим следующие выражения:
 (2.34)
(2.34)
В результате умножения генерирующего соотношения на новую переменную получают так называемый определяющий контраст. Для указанных выше полуреплик определяющими контрастами будут выражения (2.34). Зная определяющий контраст, можно найти соотношения, задающие совместные оценки. Для этого необходимо помножить независимые переменные х1, х2 и х3 на определяющий контраст.
Умножая определяющие контрасты (2.34) на х1; получим соотношения

Умножая определяющие контрасты на х2 и х3, получаем следующие соотношения


Это означает, что коэффициенты регрессии будут оценками
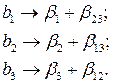
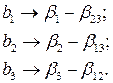
Определяющим контрастом полуреплики является соотношение
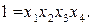
Совместные оценки будут определяться следующим образом:
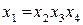

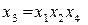
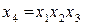
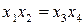
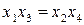
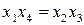
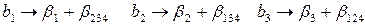
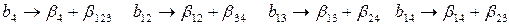 .
.
Таблица 2.17
Полуреплика 24-1 с определяющим контрастом 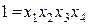
| Номер опыта | X 0 | X 1 | Х2 | Х3 | X 4 | Y |
| 1 | + | – | – | + | + | Y 1 |
| 2 | + | + | – | + | – | Y2 |
| 3 | + | – | + | + | – | Y3 |
| 4 | + | + | + | + | + | Y4 |
| 5 | + | – | – | – | + | Y 5 |
| 6 | + | + | – | – | – | Y 6 |
| 7 | + | – | + | – | – | Y 7 |
| 8 | + | + | + | – | + | Y 8 |
Таблица 2.18
Полуреплика 24-1 с определяющим контрастом 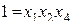
| Номер опыта | X 0 | X 1 | Х2 | Х3 | X 4 | Y |
| 1 | + | – | – | + | + | Y 1 |
| 2 | + | + | – | + | – | Y2 |
| 3 | + | – | + | + | – | Y3 |
| 4 | + | + | + | + | + | Y4 |
Окончание таблицы 2.18
| 5 | + | – | – | – | + | Y 5 |
| 6 | + | + | – | – | – | Y 6 |
| 7 | + | – | + | – | – | Y 7 |
| 8 | + | + | + | – | + | Y 8 |
Полуреплика 24-1 может быть также задана генерирующим соотношением X 4= X 1 Х2. Матрица планирования этой полуреплики представлена в табл. (2.18).
Определяющим контрастом полуреплики является соотношение
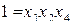
Совместные оценки в этом случае будут следующие:
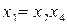
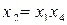
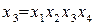
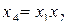
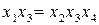
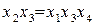
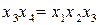

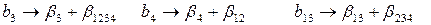
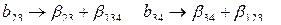
В практических задачах тройные и более высокого порядка взаимодействия значительно чаще, чем двойные, бывают равны нулю, и ими обычно можно пренебречь .
Полуреплика 24-1, заданная генерирующим соотношением 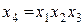 , позволяет получить раздельные оценки четырех линейных эффектов и три совместные оценки парных взаимодействий. В этом случае раздельными оценками будут
, позволяет получить раздельные оценки четырех линейных эффектов и три совместные оценки парных взаимодействий. В этом случае раздельными оценками будут 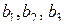 и
и 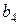 так как тройными взаимодействиями, вследствие их незначимости, можно пренебречь. В полуреплике, заданной генерирующим соотношением
так как тройными взаимодействиями, вследствие их незначимости, можно пренебречь. В полуреплике, заданной генерирующим соотношением 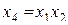 , три линейных эффекта, а именно
, три линейных эффекта, а именно 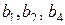 – оказались смешанными с парными взаимодействиями.
– оказались смешанными с парными взаимодействиями.
Разрешающая способность полуреплики, заданной генерирующим соотношением 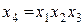 получилась значительно выше, чем у полуреплики, заданной генерирующим соотношением
получилась значительно выше, чем у полуреплики, заданной генерирующим соотношением 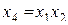 . Следовательно, разрешающая способность полуреплики зависит от генерирующего соотношения, которым она задана. Таким образом, получили весьма сложную систему смешивания.
. Следовательно, разрешающая способность полуреплики зависит от генерирующего соотношения, которым она задана. Таким образом, получили весьма сложную систему смешивания.
Все линейные эффекты оказались смешанными с несколькими парными взаимодействиями, поэтому разрешающая способность дробной реплики очень низкая. Пользоваться такой репликой можно лишь в том случае, если все парные взаимодействия близки к нулю.
Выбор дробной реплики зависит от конкретной задачи. Для получения линейной модели рекомендуют выбирать дробные реплики с возможно большей разрешающей способностью, т. е. реплики, у которых линейные эффекты смешаны с эффектами взаимодействия, близкими к нулю.
При выборе дробной реплики важно учитывать насыщенность плана, т. е. соотношение между числом опытов и числом коэффициентов, определяемых по результатам этих опытов.
Дробная реплика, полученная заменой всех эффектов взаимодействия новыми факторами, называется насыщенной. Применение насыщенных планов требует минимального числа опытов.
Число опытов в матрице насыщенной дробной реплики равно числу коэффициентов линейной модели.
Дробные реплики широко применяют при получении линейных моделей.
Эффективность применения дробных реплик зависит от удачного выбора системы смешивания линейных эффектов с эффектами взаимодействия.
При построении дробных реплик используют следующее правило: новый фактор, введенный в планирование, нужно поместить в столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь.
Планирование и реализация многофакторного эксперимента второго порядка.
3.1 Центральные композиционные планы
В процессе реализации центрального композиционного ортогонального плана функцию отклика в области оптимума обычно удается аппроксимировать полиномом второй степени вида
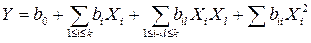 .
.
Для оценки всех коэффициентов полинома второй степени необходимо, чтобы в плане эксперимента каждый фактор принимал не менее трех значений. Применение планов типа 3k связано с большим числом опытов. Более рациональным является центральное композиционное планирование.
Центральный композиционный план второго порядка получают достройкой некоторого количества точек к «ядру», образованному линейным планом. При числе k факторов менее пяти за «ядро» центрального композиционного плана обычно принимают план полного факторного эксперимента типа 2 k .
Если число факторов более пяти, то за «ядро» центрального композиционного плана принимают полуреплику от полного факторного эксперимента.
Такой выбор «ядра» центрального композиционного плана обусловлен тем, что от «ядра» плана требуется раздельная оценка всех линейных эффектов и парных эффектов взаимодействия.
Для двух факторов центральный композиционный план второго порядка может быть представлен следующей схемой (рис. 3.1). К полному факторному эксперименту 22 (точки 1, 2, 3, 4) добавляют некоторое число n 0 опытов в центре плана (точка 9) и четыре «звездных» точки 5, 6,7,8 с координатами ( + 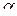 ; 0); (–
; 0); (– 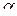 ; 0); (0, +
; 0); (0, + 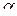 ); (0;–
); (0;– 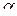 ).
).
План второго порядка для двух факторов может быть представлен матрицей (табл.3.1).
Чтобы получить центральный композиционный план второго порядка для трех факторов, к полному факторному эксперименту 23 добавляют шесть «звездных» точек с координатами ( + 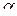 ; 0; 0); (–
; 0; 0); (– 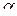 ; 0; 0); (0; +
; 0; 0); (0; + 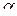 ; 0); (0; –
; 0); (0; – 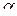 ; 0); (0; 0; +
; 0); (0; 0; + 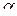 ); (0; 0; –
); (0; 0; –  ) и некоторое число n0 точек в центре плана.
) и некоторое число n0 точек в центре плана.
Центральный композиционный план второго порядка для трех факторов может быть выражен матрицей (табл. 3.2).
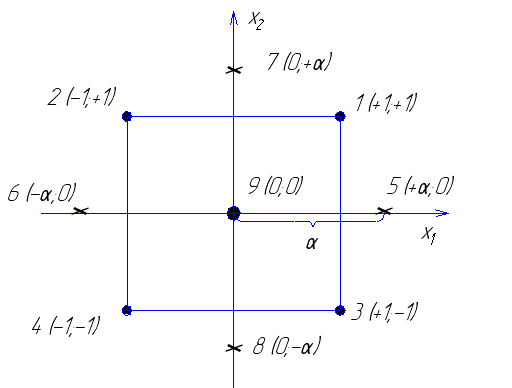
Рис. 3.1. Схема центрального композиционного плана второго порядка
для двух факторов
Таблица 3.1
Матрица центрального композиционного плана второго порядка для двух факторов
| Содержание плана | Номер опыта | x 0 | x 1 | x 2 | x 1 x 2 | x 1 2 | x 2 2 | y |
| План Типа 22 | 1 | + | + | + | + | + | + | y 1 |
| 2 | + | – | + | – | + | + | y2 | |
| 3 | + | + | – | – | + | + | y3 | |
| 4 | + | – | – | + | + | + | y4 | |
| «Звездные» точки | 5 | + | 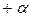
| 0 | 0 | 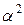
| 0 | y 5 |
| 6 | + | 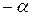
| 0 | 0 | 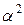
| 0 | y 6 | |
| 7 | + | 0 | 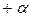
| 0 | 0 | 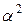
| y 7 | |
| 8 | + | 0 | 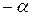
| 0 | 0 | 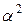
| y 8 | |
| Нулевая точка | 9 | + | 0 | 0 | 0 | 0 | 0 | y9 |
Общее число N опытов центрального композиционного плана; зависит от числа k факторов и определяется по выражению 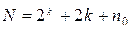 .
.
Величину «звездного» плеча 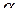 и число опытов n0 в центре плана выбирают в зависимости от принятого критерия оптимальности. За критерий оптимальности обычно принимают ортогональность или ротатабельность плана.
и число опытов n0 в центре плана выбирают в зависимости от принятого критерия оптимальности. За критерий оптимальности обычно принимают ортогональность или ротатабельность плана.
Таблица 3.2
Матрица центрального композиционного плана второго порядка для трех факторов
| Содержание плана | Номер опыта | x 0 | x 1 | x 2 | x 3 | x 1 x 2 | x 1 x 3 | x 2 x 3 | x1 2 | x 2 2 | x3 2 | y | ||
| План Типа 23 | 1 | + | + | + | + | + | + | + | + | + | + | y 1 | ||
| 2 | + | - | + | + | - | - | + | + | + | + | y2 | |||
Окончание таблицы 3.2
|
| 3 | ++ | ++ | –– | ++ | – | + | – | ++ | ++ | У+ | Y у 3 |
| 4 | ++ | –– | –– | ++ | + | – | – | ++ | ++ | ++ | y у 4 | |
| 5 | ++ | ++ | ++ | –– | + | – | – | ++ | ++ | ++ | y у5 | |
| 6 | ++ | –– | –+ | –– | – | + | – | ++ | ++ | ++ | y у6 | |
| 7 | ++ | –+ | –– | –– | – | – | + | ++ | ++ | ++ | Y у7 | |
| 8 | ++ | +– | +– | +– | + | + | + | ++ | ++ | ++ | y у8 | |
| «Звездные» точки
| 9 | ++ | 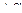 +α +α
| 00 | 00 | 0 | 0 | 0 | 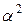 α² α²
| 00 | 00 | y у 9 |
| 10 | ++ | 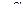 -α -α
| 00 | 00 | 0 | 0 | 0 | 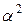 α² α²
| 00 | 00 | y у10 | |
| 11 | ++ | 00 | 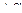 +α +α
| 00 | 0 | 0 | 0 | 00 | 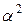 α² α²
| 00 | y у11 | |
| 12 | ++ | 00 | 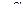 -α -α
| 00 | 0 | 0 | 0 | 00 | 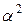 α² α²
| 00 | y у12 | |
| 13 | ++ | 00 | 00 | 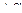 +α +α
| 0 | 0 | 0 | 00 | 00 | 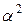 α² α²
| y у13 | |
| 14 | ++ | 00 | 00 | 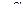 -α -α
| 0 | 0 | 0 | 00 | 00 | 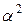 α² α²
| y у14 | |
| Нулевая точка | 15 | ++ | 00 | 00 | 00 | 0 | 0 | 0 | 00 | 00 | 00 | y у15 |
3.2. Ортогональные планы
Преимущество ортогональных планов состоит в малом объеме вычислений, тан как все коэффициенты регрессии определяются независимо друг от друга.
В ортогональных планах сумма построчных произведений элементов двух любых столбцов матрицы планирования равна нулю.
В матрице центрального композиционного плана не все столбцы ортогональны, так как
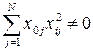 (3.2)
(3.2)
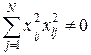 (3.3)
(3.3)
x0 всегда равно +1, а 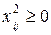 .
.

Рис. 3.2 Схема центрального композиционного плана второго порядка для трех факторов.
Например, матрица, представленная в табл 3.1, не ортогональна, ибо

Для ортогонализации соотношения (3.2) необходимо преобразовать столбцы матрицы, заменив  новой переменной
новой переменной 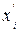 . Новую переменную находят по выражению
. Новую переменную находят по выражению
 . (3.3)
. (3.3)
После замены 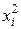 на
на 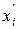 будут равны нулю суммы построчных произведений столбцов:
будут равны нулю суммы построчных произведений столбцов:
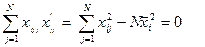 . (3.4)
. (3.4)
Так, например, в матрице центрального композиционного плана для двух факторов (табл. 3.1) получаем новые переменные
 . (3.5)
. (3.5)
Тогда
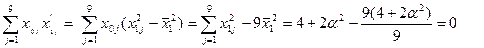 .
.
Аналогично
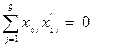 .
.
Ортогонализация соотношения (3.3) достигается выбором «звездного» плеча 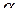 . Значения «звездного» плеча, вычисленные для различного числа факторов, приведены в табл. 3.3.
. Значения «звездного» плеча, вычисленные для различного числа факторов, приведены в табл. 3.3.
Если ортогональность принять за достаточный критерий оптимальности плана эксперимента, то на число опытов в центре плана не накладывается какого-либо ограничения, и обычно n 0 = 1.
Таблица 3.3
Величина «звездного» плеча 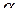
| Число независимых переменных | Ядро плана | Число дополнительных опытов | Величина плеча 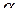
|
| 2 | 22 | 5 | 1,000 |
| 3 | 23 | 7 | 1,215 |
| 4 | 24 | 9 | 1,414 |
| 5 | 25-1 | 11 | 1,547 |
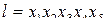
Подставляя 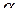 =1 в соотношения (3.5), находим новые переменные
=1 в соотношения (3.5), находим новые переменные 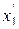 и
и 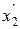
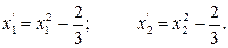
Тогда ортогональный центральный композиционный план второго порядка для двух факторов может быть представлен матрицей (табл. 3.4)
При трех факторах 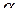 = 1,215.
= 1,215.
Используя соотношение (3.3) и матрицу плана второго порядка для трех факторов (табл3.2) находим новые переменные 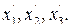
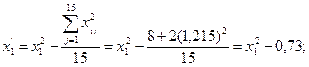
Аналогично
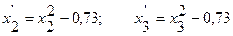 .
.
Таблица 3.4
Ортогональный центральный композиционный план второго порядка для двух факторов
| Содержание плана | Номер операции | x 0 | x 1 | x 2 | x 1 x 2 | x 1 2 -2/3 | x 2 2 -2/3 | y |
| План типа 22 | 1 | + | + | + | + | + 1/3 | + 1/3 | y 1 |
| 2 | + | – | + | – | + 1/3 | + 1/3 | y2 | |
| 3 | + | + | – | – | + 1/3 | + 1/3 | y3 | |
| 4 | + | – | – | + | + 1/3 | + 1/3 | y4 | |
| «Звездные» точки с плечом | 5 | + | + | 0 | 0 | + 1/3 | – 2/3 | y 5 |
| 6 | + | – | 0 | 0 | + 1/3 | – 2/3 | y 6 | |
| 7 | + | 0 | + | 0 | – 2/3 | + 1/3 | y 7 | |
| 8 | + | 0 | – | 0 | – 2/3 | + 1/3 | y 8 | |
| Нулевая точка | 9 | + | 0 | 0 | 0 | – 2/3 | – 2/3 | y9 |
Матрица ортогонального планирования для трех факторов представлена в таблице 3.5. Благодаря ортогональности матрицы планирования коэффициенты регрессии определяются независимо друг от друга по формуле
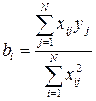 ;
;
где i – номер столбца матрицы;
j – номер опыта;
xij – элементы соответствующего столбца матрицы;
yi – значение параметра оптимизации в i-м опыте.
Дисперсии коэффициентов регрессии определяются по формуле
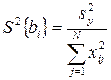 .
.
Дисперсии коэффициентов не равны, так как суммы квадратов элементов столбцов матрицы 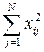 не равны друг другу.
не равны друг другу.
Реализация опытов по матрице планирования с квадратичной переменной позволяет построить модель вида:

Неизвестный коэффициент b 0 находят по выражению
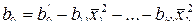
с дисперсией
 .
.
Таблица 3.5
Матрица центрального композиционного плана второго порядка
для трех факторов
| Содержание плана | № Опыта | x х0 | x х1 | x х2 | x х3 | x х1 x 2 | x х1 x 3 | x х2 x 3 | x 1 2 -0,73 | x 2 2 -0,73 | x 3 2 -0,73 | y |
| План 2³ | 1 | + | + | + | + | + | + | + | +0,27 | +0,27 | +0,27 | y 1 |
| 2 | + | – | + | + | – | + | – | +0,27 | +0,27 | +0,27 | y2 | |
| 3 | + | + | – | + | – | – | + | +0,27 | +0,27 | +0,27 | y3 | |
| 04 | –+ | – | – | + | + | – | – | +0,27 | +0,27 | +0,27 | y4 | |
| 05 | –+ | + | + | – | + | – | – | +0,27 | +0,27 | +0,27 | y 5 | |
| 06 | –+ | – | + | – | – | + | – | +0,27 | +0,27 | +0,27 | y 6 | |
| 07 | –+ | + | – | – | – | – | + | +0,27 | +0,27 | +0,27 | y 7 | |
| 8 | + | – | – | – | + | + | + | +0,27 | +0,27 | +0,27 | y 8 | |
| Окончание таблицы 3.5 | ||||||||||||
|
«Звездные» точки с | 09 | –+ | +1,215 | 0 | 0 | 0 | 0 | 0 | +0,746 | – 0,73 | – 0,73 | y9 |
| 110 | + | –1,215 | 0 | 0 | 0 | 0 | 0 | +0,746 | – 0,73 | – 0,73 | y 10 | |
| 111 | + | 0 | +1,215 | 0 | 0 | 0 | 0 | – 0,73 | +0,746 | – 0,73 | y 11 | |
| 112 | + | 0 | –1,215 | 0 | 0 | 0 | 0 | – 0,73 | +0,746 | – 0,73 | y 12 | |
| 113 | + | 0 | 0 | +1,215 | 0 | 0 | 0 | – 0,73 | – 0,73 | +0,746 | y 13 | |
| 114 | + | 0 | 0 | –1,215 | 0 | 0 | 0 | – 0,73 | – 0,73 | +0,746 | y 14 | |
| Нулевая точка | 115 | + | 0 | 0 | 0 | 0 | 0 | 0 | – 0,73 | – 0,73 | – 0,73 | y 15 |
Проверка адекватности уравнения второго порядка, получаемого после центрального композиционного ортогонального планирования, производится так же, как и проверка адекватности линейной модели, полученной при реализации плана первого порядка.
3.3 Ротатабельное планирование
Критерий ортогональности не является достаточно сильным критерием оптимизации центрального композиционного плана второго порядка.
Информация о поверхности отклика, полученная при ортогональном планировании второго порядка, различна в разных направлениях. В то же время исследователь, начиная эксперимент, чаще всего не знает, какое направление будет представлять преимущественный интерес.
В тех случаях, когда нет достоверной информации об ориентации поверхности отклика, наиболее разумным является использование центральных композиционных планов, отвечающих требованию рототабельности, т. е. планов, позволяющих получать модель, способную предсказывать значение параметра оптимизации с одинаковой точностью независимо от направления на равных расстояниях от центра плана.
Ротатабельность центрального композиционного плана достигается выбором величины «звездного» плеча 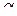 . Величину звездного плеча для «ядра», содержащего полный факторный эксперимент, определяют из соотношения
. Величину звездного плеча для «ядра», содержащего полный факторный эксперимент, определяют из соотношения
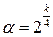 , (3.6)
, (3.6)
а для «ядра», содержащего дробную реплику,
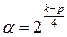 . (3.7)
. (3.7)
Для ротатабельного планирования второго порядка важное значение имеет выбор числа опытов в центре плана, так как число опытов в центре плана определяет характер распределения получаемой информации о поверхности отклика.
Число опытов в центре плана выбирается таким, чтобы обеспечивалось так называемое униформ-планирование.
Планирование называется униформ-ротатабельным, если получаемая информация постоянно остается внутри интервала 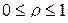 , где
, где 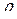 – радиус информационного контура.
– радиус информационного контура.
Униформ-ротатабельное планирование возможно, если некоторая константа 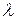 не превышает единицы (немного меньше ее):
не превышает единицы (немного меньше ее):
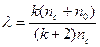 , (3.8)
, (3.8)
где
n 0 – число опытов в центре плана(число нулевых точек);
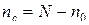 ;
;
N – общее число опытов;
k – число факторов.
Все данные, необходимые для построения матриц центрального композиционного ротатабельного планирования второго порядка при числе факторов от двух до семи, табулированы (таблица 3.6).
Матрица ротатабельного униформ - планирования второго порядка для k = 2 приведена в табл. 3.7.
Матрицы ротатабельного планирования второго порядка не ортогональны, поэтому объем вычислительной работы при определении коэффициентов регрессии довольно велик.
Таблица 3.6
Данные для построения матриц центрального композиционного ротатабельного
планирования второго порядка
| Число факторов k | «Ядро» плана | Число точек «ядра» n я | Число
«звездных»
точек 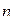
| Число
нулевых
точек 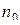
| Величина
«звездного»
плеча 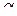
| Общее число опытов N |
| 2 | 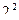
| 4 | 4 | 5 | 1,414 | 13 |
| 3 | 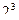
| 8 | 6 | 6 | 1,682 | 20 |
| 4 | 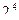
| 16 | 8 | 7 | 2,000 | 31 |
| 5 | 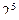
| 32 | 10 | 10 | 2,378 | 52 |
| 5 | 
| 16 | 10 | б | 2,000 | 32 |
| 6 | 
| 64 | 12 | 15 | 2,828 | 91 |
| 6 | 
| 32 | 12 | 9 | 2,378 | 53 |
| 7 | 
| 128 | 14 | 21 | 3,363 | 163 |
| 7 | 
| 64 | 14 | 14 | 2,828 | 92 |
Вычисление коэффициентов регрессии рекомендуется проводить с помощью электронных вычислительных машин, используя метод наименьших квадратов.
Коэффициенты уравнения регрессии определяют по формулам:
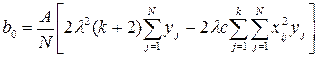 ; (3.9)
; (3.9)
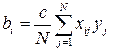 ; (3.10)
; (3.10)
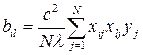 ; (3.11)
; (3.11)
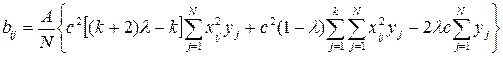 . (3.12)
. (3.12)
Таблица 3.7
Матрица ротатабельного униформ - планирования для k = 2
| № Опыта | x х0 | x 1 | x 2 | х1 х2 | 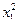 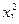
|
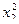
| y | № Опыта | x0 | x1 | x2 | х1 х2 |  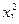
|
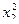
| y |
| 1 | + | + | + | + | + | + | y1 | 8 | + | 0 | –1,414 | 0 | 0 | 2 | y8 |
| 2 | + | – | + | – | + | + | y2 | 9 | + | 0 | 0 | 0 | 0 | 0 | y9 |
| 3 | + | + | – | – | + | + | y3 | 10 | + | 0 | 0 | 0 | 0 | 0 | y10 |
| 4 | + | – | – | + | + | + | y4 | 11 | + | 0 | 0 | 0 | 0 | 0 | y11 |
| 5 | + | +1,414 | 0 | 0 | 2 | 0 | y5 | 12 | + | 0 | 0 | 0 | 0 | 0 | y12 |
| 6 | + | –1,414 | 0 | 0 | 2 | 0 | y6 | 13 | + | 0 | 0 | 0 | 0 | 0 | y13 |
| 7 | + | 0 | +1.414 | 0 | 0 | 2 | y7 |
где
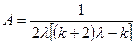 ;
; 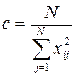 .
.
Дисперсии коэффициентов уравнения регрессии находят по формулам
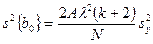 ; (3.13)
; (3.13)
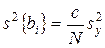 ; (3.14)
; (3.14)
 ; (3.15)
; (3.15)
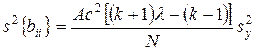 . (3.16)
. (3.16)
Вычислив коэффициенты уравнения регрессии, определяют их доверительные интервалы. После этого, исключив из уравнения статистически незначимые коэффициенты, получают математическую модель. Адекватность полученной модели проверяют с помощью расчетного критерия Фишера
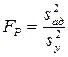 .
.
Дисперсию параметра оптимизации определяют по результатам опытов в центре плана:
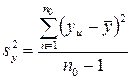 ,
,
где п0 – число параллельных опытов в центре плана; уи – значение параметра оптимизации в и-м опыте; 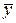 – среднее арифметическое значение параметра оптимизации в п0 опытах; и – номер параллельного опыта в центре плана.
– среднее арифметическое значение параметра оптимизации в п0 опытах; и – номер параллельного опыта в центре плана.
Для определения 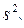 вычисляют сумму sR квадратов отклонений расчетных
вычисляют сумму sR квадратов отклонений расчетных 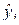 значений функции отклика от экспериментальных
значений функции отклика от экспериментальных 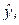 :
:
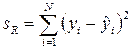 .
.
Из полученной суммы sR вычитают сумму sE, использованную для определения дисперсии параметра оптимизации по результатам опытов в центре плана:
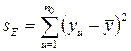 . (3.17)
. (3.17)
Полученный результат (s R – sE) делят на число степеней свободы 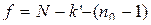 , где к' – число статистически значимых коэффициентов регрессии. Таким образом,
, где к' – число статистически значимых коэффициентов регрессии. Таким образом,
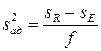 . (3.18)
. (3.18)
Если FP<FT (при выбранном уровне значимости), то гипотеза адекватности модели принимается. Если гипотеза адекватности модели не принимается, то применяют планирование третьего порядка или повторяют все опыты, сузив интервалы варьирования или изменив основные уровни факторов.
Дата: 2018-12-28, просмотров: 643.