При исследовании процессов резания многие зависимости традиционно представляют уравнениями степенного вида [3]. Например, зависимость стойкости режущего инструмента от элементов режима резания часто выражают уравнением
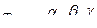 , (4.20)
, (4.20)
где υ – скорость резания; s – подача; t – глубина резания; с, α, β, γ – постоянные величины.
Уравнение (4.20) в результате логарифмирования линеаризуется:
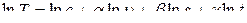 . (4.21)
. (4.21)
Уравнение (4.21) можно выразить следующим образом:
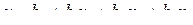 , (4.22)
, (4.22)
где 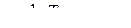 – кодированные значения υ, s , t.
– кодированные значения υ, s , t.
Кодированное значение xi фактора
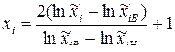 , (4.23)
, (4.23)
где  – натуральное значение;
– натуральное значение; 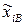 ,
, 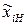 – натуральные значения верхнего и нижнего уровней, соответственно.
– натуральные значения верхнего и нижнего уровней, соответственно.
Для оценки коэффициентов уравнения (4.22) удобно использовать результаты многофакторного эксперимента. При этом результаты опытов обычно представляют полиномом вида
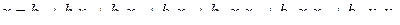 (4.24)
(4.24)
или полиномом вида
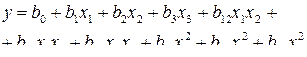 (4.25)
(4.25)
После определения коэффициентов уравнения (4.24) или уравнения (4.25) необходимо проверить гипотезу адекватности линейной части этих полиномов. Если гипотеза подтверждается, т.е. уравнение 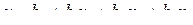 адекватно, то, подставляя в это уравнение значения
адекватно, то, подставляя в это уравнение значения 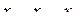 , определяемые соотношением (4.23), получим выражение (4.21). Если гипотеза адекватности уравнения
, определяемые соотношением (4.23), получим выражение (4.21). Если гипотеза адекватности уравнения 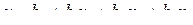 не подтверждается, то необходимо проверить гипотезу адекватности уравнения (4.24) или (4.25). В случае, если уравнения (4.24) или (4.25) окажутся неадекватными, можно будет предложить другую модель, характеризующую зависимость стойкости инструмента от исследуемых факторов.
не подтверждается, то необходимо проверить гипотезу адекватности уравнения (4.24) или (4.25). В случае, если уравнения (4.24) или (4.25) окажутся неадекватными, можно будет предложить другую модель, характеризующую зависимость стойкости инструмента от исследуемых факторов.
Рассмотрим одну из задач, в которой математическая модель процесса представлена уравнением степенного вида. Исследовали процесс хонингования отверстий.
Требовалось установить влияние окружной скорости υ0 хона, скорости υп его возвратно- поступательного движения и давления ру на шероховатость поверхности.
Было сделано предположение, что зависимость шероховатости Rа поверхности от исследуемых факторов можно представить уравнением регрессии степенного вида
 . (4.26)
. (4.26)
Уравнение (4.26) после логарифмирования получит вид
 . (4.27)
. (4.27)
Если результаты эксперимента выразить полиномом вида
 , (4.28)
, (4.28)
где  , а
, а  – кодированные значения факторов υ0, υп, ру, то справедливость зависимости (4.26) можно установить проверкой адекватности линейной части полинома (4.28).
– кодированные значения факторов υ0, υп, ру, то справедливость зависимости (4.26) можно установить проверкой адекватности линейной части полинома (4.28).
Таблица 4.12
Уровни факторов
| Факторы | Кодированное обозначение | Натуральные уровни факторов, соответствующие кодированным | ||
| верхний +1 | Основной 0 | нижний –1 | ||
| Окружная скорость хона υ0, м/мин | x1 | 137,5 | 98,5 | 70,7 |
| Скорость υп возвратно-поступательного движения хона, м/мин | x2 | 16 | 10,6 | 7 |
| Давление брусков ру, Па | x3 | 980665 | 617819 | 392266 |
Принятые в исследовании уровни факторов и их кодовые обозначения указаны в табл. 4.12. Кодированные значения факторов  будут равны единице на верхнем уровне, нулю на основном уровне и минус единице на нижнем уровне, при натуральных значениях факторов, указанных в табл. 4.12. Изложенное обусловлено формулой (4.23), которая для каждого из факторов получит соответственно следующий вид
будут равны единице на верхнем уровне, нулю на основном уровне и минус единице на нижнем уровне, при натуральных значениях факторов, указанных в табл. 4.12. Изложенное обусловлено формулой (4.23), которая для каждого из факторов получит соответственно следующий вид
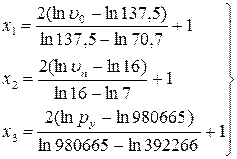 (4.29)
(4.29)
Для оценки коэффициентов уравнения (4.28) проведен полный факторный эксперимент типа 23. Матрица планирования и результаты опытов указаны в табл.4.13.
Таблица 4.13
Матрица планирования и результаты опытов
| № опыта | x0 | x1 | x2 | x 3 | x1 x2 | x1 x 3 | x 2 x 3 | x1 x 2 x 3 | y | № опыта | x0 | x1 | x2 | x 3 | x1 x2 | x1 x 3 | x 2 x 3 | x1 x 2 x 3 | y |
| 1 | + | – | – | – | + | + | + | – | 0,449 | 5 | + | – | – | + | + | – | – | + | 0,688 |
| 2 | + | + | – | – | – | – | + | + | 0,228 | 6 | + | + | – | + | – | + | – | – | 0,515 |
| 3 | + | – | + | – | – | + | – | + | 0,233 | 7 | + | – | + | + | – | – | + | – | 0,445 |
| 4 | + | + | + | – | + | – | – | – | –0,347 | 8 | + | + | + | + | + | + | + | + | 0,129 |
В результате обработки экспериментальных данных получено уравнение:
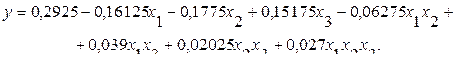 (4.30)
(4.30)
Дисперсия воспроизводимости, вычисленная по результатам четырех опытов в центре плана, 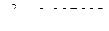 . Дисперсия коэффициентов уравнения регрессии
. Дисперсия коэффициентов уравнения регрессии 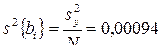 . Доверительный интервал Δ bi коэффициентов
. Доверительный интервал Δ bi коэффициентов
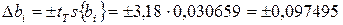 ,
,
где tT =3,18 при 5%-ном уровне значимости и числе степеней свободы f =3.
Коэффициенты  по абсолютной величине меньше доверительного интервала, поэтому их можно считать статистически незначимыми и исключить из уравнения регрессии. После исключения незначимых коэффициентов уравнение (4.30) приняло вид
по абсолютной величине меньше доверительного интервала, поэтому их можно считать статистически незначимыми и исключить из уравнения регрессии. После исключения незначимых коэффициентов уравнение (4.30) приняло вид
 . (4.31)
. (4.31)
Для проверки адекватности уравнения (4.31) вычисляем дисперсию 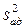 адекватности:
адекватности:
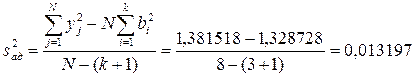 .
.
Адекватность уравнения (4.31) проверяем по F-критерию. Находим расчетное значение F-критерия:
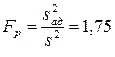 .
.
Табличное значение FT-критерия при 5%-ном уровне значимости и числах степеней свободы f1=4 и f2=3 равно 9,1. Так как FP < FT, то линейная модель адекватна. Следовательно, зависимость шероховатости поверхности от исследуемых факторов процесса хонингования с достаточной точностью можно представить уравнением (4.26).
Для перехода от кодированных значений факторов к натуральным в уравнение (4.31) подставляем значения факторов 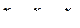 по выражениям (4.29).
по выражениям (4.29).
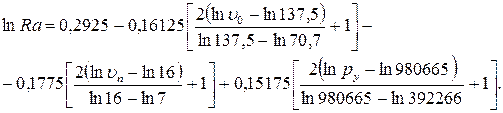
После преобразования получим
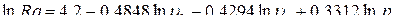 . (4.32)
. (4.32)
Потенцируя выражение (4.32) находим зависимость шероховатости поверхности от исследуемых факторов процесса хонингования:
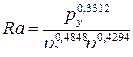 .
.
Дата: 2018-12-28, просмотров: 435.