ГУСЕВ В. Г.
ТЕОРИЯ И ПРАКТИКА ПЛАНИРОВАНИЯ
МНОГОФАКТОРНЫХ ЭКСПЕРИМЕНТОВ
Владимир 2010
УДК 621: 658.5.012.1
Рецензент
Заслуженный изобретатель Российской Федерации, доктор технических наук, профессор Денисенко В.И.
Печатается по решению редакционно-издательского совета Владимирского государственного университета
Гусев В.Г. Теория и практика планирования многофакторных экспериментов:
Учебное пособие. - Владимирский государственный университет:
Владимир, 2010.
Составлены в соответствии с требованиями государственного образовательного стандарта высшего профессионального образования. Изложены основные принципы и научные положения теории планирования линейных многофакторных экспериментов, экспериментов второго порядка, методология их практической реализации и статистической обработки результатов на конкретных примерах исследования процессов механической обработки изделий машиностроения.
Предназначены для магистрантов дневной формы обучения по направлению «Технология, оборудование и автоматизация машиностроительного производства», а также аспирантов, обучающихся по специальностям: 05.03.01 - «Технологии и оборудование механической и физико-технической обработки», 05.02.08 - «Технология машиностроения», а также по другим техническим специальностям. Ил. Табл.
ПРЕДИСЛОВИЕ
В ходе разработки технических устройств и систем, технологических процессов механической и физико-технической обработки, сборки и испытания его создателям приходится решать множество научно-технических задач, различных по уровню сложности и объему. При этом часто встречаются задачи, связанные с выбором наиболее правильного технического решения и нахождением оптимальных значений всех параметров и характеристик.
Сказанное в полной мере относится к исследованиям различного рода явлений, протекающих в механических и других объектах и системах.
В настоящее время большое количество молодых специалистов с высшим образованием, приходящих на работу в научно-производственные предприятия, занимающиеся созданием новой техники и технологии, недостаточно подготовлены к поиску новых технических решений и их использованию при разработке конкретной продукции.
Такая ситуация в значительной мере обусловлена недостаточным вниманием существующих государственных стандартов высшего профессионального инженерного образования к изучению современных методов научных исследований и, в частности, к теории планирования многофакторных экспериментов и оптимизации важнейших параметров проектируемой техники и технологии.
Имея достаточно хорошую компьютерную подготовку, используемую для создания технических объектов и технологических процессов, они часто не владеют методикой подготовки, проведения многофакторных экспериментов, статистической обработки результатов и оптимизации полученных математических моделей.
Отсутствие конкретных знаний и навыков в области оптимизации технических и технологических решений отражается непосредственно на научно-техническом уровне, а, следовательно, на конечных результатах исследований и разработок.
При переходе к двух-уровневой подготовке молодых специалистов с высшим образованием (бакалавров и магистров) остро встает вопрос овладения современными методами научного творчества, поиска новых решений и оптимизации моделей, описывающих изучаемые объекты, явления и процессы. Значительную роль в процессе формирования основополагающих знаний и практических навыков бакалавров и магистров в области эффективного использования научных методов исследований играет методология планирования и реализации экстремальных экспериментальных исследований. Настоящее учебное пособие направлено на теоретическую и практическую подготовку магистрантов, аспирантов в области планирования и реализации экстремальных многофакторных экспериментов, оптимизации многофакторных систем и технологических процессов механической обработки различных изделий машиностроения с наименьшими затратами.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1 Понятия и характеристика однофакторного и многофакторного экспериментов, понятие планирования экспериментов
Для адекватного восприятия читателями излагаемого в настоящем учебном пособии материала дадим определение и понятие основных терминов и физических величин, применяемых в теории и практике планирования многофакторных экспериментов.
Эксперимент - понятие, которое произошло от латинского слова experimentum , что означает пробу, опыт. В словаре иностранных слов дано следующее определение: эксперимент - научно поставленный опыт, наблюдение в точно учитываемых условиях, позволяющих следить за ходом явления и воссоздавать его каждый раз при повторении этих условий. В энциклопедическом словаре эксперимент определен как чувственно-предметная деятельность в науке. Второе определение более широкое. Первое - более подходит к существу дисциплины "Теория планирования многофакторных экспериментов".
Эксперимент бывает однофакторный, многофакторный, физический, модельный и др. Однофакторный эксперимент - такой эксперимент, когда при изменении одной независимой переменной (фактора) и стабилизации всех остальных независимых переменных, фиксируют значения изучаемой зависимой переменной (параметра). Обработав результаты однофакторного эксперимента, находят зависимость исследуемого параметра только от одного фактора. Производя большое число однофакторных экспериментов при изучении многофакторной системы, получают частотные зависимости, представленные многими графиками, имеющими иллюстративный характер. Найденные таким образом частные зависимости невозможно объединить в одну общую модель процесса.
Использование однофакторного эксперимента для всестороннего исследования многофакторного процесса требует постановки очень большого числа опытов. Для их выполнения в ряде случаев необходимо значительное время, в течение которого влияние неконтролируемых факторов на результаты опытов может существенно измениться. Отсюда следует, что результаты однофакторных экспериментов, полученные при исследовании многофакторных систем, малопригодны для практического использования. Кроме того, при решении экстремальных задач данные значительного числа опытов однофакторного эксперимента оказываются ненужными, так как
получены они для области, далекой от оптимума.
Однофакторные эксперименты не отражают реальной картины явлений и процессов, протекающих в природе, поскольку они проводятся в искусственно созданных условиях, значительно отличающихся от условий многофакторного эксперимента. Для природы характерно изменение одновременно нескольких факторов, которые влияют на выходной параметр системы. В качестве примера может служить нагрев солнечными лучами воздушных масс, при котором одновременно с повышением температуры воздуха происходит изменение скорости и направления движения воздушных масс, изменение давления, влажности и др.
Приведенный пример свидетельствует о существовании многофакторных процессов, систем и объектов, изучение которых посредством однофакторных экспериментов не дает реальной картины их поведения, а поэтому результатами однофакторных экспериментов в подобных случаях пользоваться нельзя. Отмеченное не означает того, что от однофакторных экспериментов следует отказаться вообще.
Однофакторные эксперименты могут использоваться, например, для определения зависимости изучаемого параметра от какого-либо фактора с целью правильного выбора исходной априорной модели при изучении многофакторных процессов и явлений; при исследовании процесса, изменение которого зависит от какой-либо одной доминирующей независимой переменной в то время как влияние других независимых переменных на процесс незначительно
В машиностроении процессы механической, физико-технической обработки в подавляющем большинстве своем являются многофакторными, поэтому подготовка, реализация многофакторных экспериментов в этих условиях является особо актуальными.
Многофакторный эксперимент – такой эксперимент, при котором варьируют одновременно все независимые переменные (факторы), оказывающие влияние на процесс или систему. В результате обработки результатов опытов получают математическую модель, связывающую изучаемую зависимую переменную (параметр) одновременно со всеми независимыми факторами. Для изучения многофакторных систем наиболее целесообразным является применение статистических методов планирования многофакторных экспериментов.
Физический эксперимент – это реальный эксперимент с использованием оборудования, установок, устройств и т. д., а также с вещественными материалами. Это наиболее трудоёмкий, энергоёмкий и дорогой вид деятельности. Планирование эксперимента зарождалось и развивалось применительно к таким областям деятельности как металлургия, машиностроение, химическая, пищевая промышленность, транспорт и др.
Модельный эксперимент – это эксперимент с использованием модели, которая может быть трёх типов:
- физической, в этом случае она может отличаться от реального объекта масштабом;
- абстрактной, неформализованной на уровне логического мышления;
- формализованной математически. Чтобы получать на основе модельного эксперимента правильные сведения об объекте исследования, нужно построить достаточно точную модель. А поскольку невозможно абсолютно точное описание влияния всех возможных независимых переменных на процесс функционирования объекта исследования, то модель, а, следовательно, и объект описываются вероятностно.
Эксперимент, который ставится для решения задач оптимизации, называется экстремальным, поскольку он связан с поиском экстремума некоторой функции.
Под планированием эксперимента понимают нахождение условий проведения опытов, их количества в многофакторном эксперименте, необходимых и достаточных для установления взаимосвязи параметра с факторами с требуемой точностью. Планирование эксперимента – это новый раздел математической статистики. В нем всесторонне рассматриваются статистические методы планирования эксперимента. Эти методы позволяют во многих случаях при минимальном числе опытов получать модели многофакторных процессов.
Высокая эффективность использования статистических методов планирования эксперимента при исследовании технологических процессов объясняется тем, что многие важные их характеристики являются случайными величинами, законы распределения которых близки к нормальному закону. Характерными особенностями процесса планирования эксперимента являются стремление минимизировать число опытов; одновременное варьирование всех исследуемых факторов по специальным правилам - алгоритмам; применение математического аппарата, формализующего многие действия исследователя; выбор стратегии, позволяющей принимать обоснованные решения.
Таким образом, планирование эксперимента - это совокупность приемов, позволяющих исследователю разумно поставить эксперимент, сообразуясь с целью исследования, со стремлением получить максимальную информацию при необходимости экономить средства (при ограниченном числе опытов), а также правильно обработать и интерпретировать результаты экспериментов.
Техника планирования: на каждом шаге ставится небольшая серия опытов, в каждом из которых варьируются по определённым правилам все факторы.
Математическая обработка результатов эксперимента позволяет выработать условия проведения следующей серии опытов, направленных к достижению оптимума. В этом суть метода Бокса–Уилсона или метода крутого восхождения. Применение планирования эксперимента, несомненно, организует и оптимизирует деятельность экспериментатора.
Планирование и реализация полного факторного эксперимента
Выбор модели
Перед проведением опытов, экспериментатор должен выбрать вид уравнения регрессии (модели). Выбор модели – это сложный процесс, связанный со многими обстоятельствами и соображениями. Как отмечалось выше, под математической моделью будем понимать функцию отклика. Выбрать модель – это значит выбрать вид этой функции, записать её уравнение. Затем спланировать и поставить эксперимент для отыскания численных значений коэффициентов уравнения.
Моделей бывает много и разных. Чтобы выбрать одну из них, надо четко знать, что мы хотим от модели, какие требования к ней предъявляем.
Исходя из выбранной стратегии, ясно, что главное требование к модели – это способность предсказывать направление дальнейших опытов с требуемой точностью. Так как до получения модели не известно, какое направление нам понадобится, то естественно требовать, чтобы точность предсказания во всех возможных направлениях была бы одинакова. Это значит, что в некоторой подобласти, в которую входят выполненные опыты, предсказанное с помощью модели значение отклика не должно отличаться больше, чем на некоторую заранее заданную величину. Модель, удовлетворяющая такому условию, называется адекватной. Если несколько различных моделей отвечает нужным требованиям, то следует выбрать ту из них, которая является самой простой. Модель выбирают на основании априорной информации либо на основании результатов предварительных экспериментов. Для двух факторов могут быть выбраны следующие виды моделей.
модель первой степени
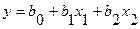 , (2.5)
, (2.5)
модель второй степени
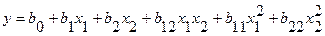 , (2.6)
, (2.6)
модель третьей степени
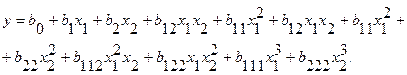 (2.7)
(2.7)
Выражения (2.5) – (2.7) называются уравнениями регрессии, а коэффициенты, стоящие перед кодовыми значениями факторов – коэффициентами регрессии. Итак, мы представили неизвестную нам функцию полиномом. Замена одной функции другой, примерно эквивалентной функцией, называется аппроксимацией. Следовательно, мы аппроксимировали неизвестную нам функцию полиномом. Но, как показано на примере, полиномы бывают различных степеней. Какой полином взять на первом шаге?
Эксперимент нужен для расчета численных значений коэффициентов регрессии. Поэтому, чем больше коэффициентов, тем больше опытов нужно поставить. Мы же стремимся сократить их число. Следовательно, надо найти полином, содержащий как можно меньше коэффициентов, но удовлетворяющий требованиям, предъявляемым к модели. При заданном числе факторов, чем ниже степень полинома, тем меньше в нем коэффициентов.
С другой стороны, нужно, чтобы модель предсказывала направление наискорейшего улучшения параметра оптимизации. Такое направление называют направлением градиента. Движение в этом направлении приведет к успеху быстрее, чем движение в любом другом направлении. В этом случае лучше использовать полином первой степени, так как он содержит информацию о направлении градиента, и, кроме того, в нем минимально возможное число коэффициентов при данном числе факторов.
Единственное опасение в том, будет ли линейная модель всегда адекватной. Однако всегда существует такая окрестность любой (почти любой) точки, в которой линейная модель адекватна. Размер такой области заранее не известен, но адекватность можно проверять по результатам эксперимента. Следовательно, выбрав сначала произвольную подобласть, мы рано или поздно найдем ее требуемые размеры. Как только это случится, воспользуемся движением по градиенту. Затем ищем линейную модель в другой подобласти. Цикл повторяется до тех пор, пока движение по градиенту не перестанет давать эффект. Это значит, что мы попали в область, близкую к оптимуму. Такая область называется «почти стационарной». Здесь линейная модель уже не нужна. Чтобы подробнее описать область оптимума, нужно перейти к полиномам более высокой степени.
Кроме задачи оптимизации, может возникать задача математического описания объекта исследования - построения интерполяционной модели. В этом случае нас не интересует оптимум. Здесь нам нужно предсказать результат с требуемой точностью во всех точках некоторой заранее заданной области. С этой целью последовательно увеличивают степень полинома до тех пор, пока модель не окажется адекватной.
Таким образом, на первой стадии экспериментальных исследований при отсутствии сведений о модели разумно выбирать модель первого порядка. Если же есть сведения о нелинейности, то принимается модель второго порядка.
Задачей планирования многофакторных экспериментов является отыскание коэффициентов регрессии, после чего модель процесса или модель функционирования устройства становится известной.
Проведение опытов
После выбора плана эксперимента, параметров оптимизации, определения уровней и интервалов варьирования факторов переходят к эксперименту.
Каждая строка матрицы – это условие опыта. Для исключения систематических ошибок рекомендуется опыты, предусмотренные матрицей, проводить в случайной последовательности, а не в той последовательности, которая приведена в колонке «номер опыта» матрицы планирования. Эта процедура носит название рандомизации эксперимента во времени.
Случайную последовательность опытов можно определить, воспользовавшись таблицей случайных чисел (табл. 2.5) или выполнив компьютерную рандомизацию. Если требуется, например, провести в случайной последовательности восемь опытов матрицы, то из случайного места таблицы (2.5) последовательно выписываем числа, лежащие в интервале от 1 до 8, при этом отбрасываем уже выписанные числа и числа, больше восьми.
Так, например, начиная с числа 87 (1-я строка табл. 2.5) [3], получаем следующую последовательность реализации опытов: 72831456 вместо последовательности: 345678.
Таблица 2.5
Фрагмент таблицы случайных чисел
| 87 | 63 | 88 | 23 | 62 | 51 | 07 | 69 | 59 | 02 | 89 | 49 | 14 |
| 07 | 76 | 85 | 37 | 84 | 37 | 47 | 32 | 25 | 21 | 15 | 08 | 82 |
| 03 | 33 | 48 | 84 | 37 | 37 | 29 | 38 | 37 | 89 | 76 | 25 | 09 |
| 13 | 01 | 59 | 47 | 64 | 04 | 99 | 59 | 96 | 20 | 30 | 87 | 31 |
| 00 | 83 | 48 | 94 | 44 | 08 | 67 | 79 | 41 | 61 | 41 | 15 | 60 |
| 24 | 07 | 78 | 61 | 89 | 42 | 58 | 88 | 22 | 16 | 13 | 24 | 40 |
| 61 | 12 | 90 | 62 | 41 | 11 | 59 | 85 | 18 | 42 | 61 | 29 | 88 |
| 27 | 84 | 05 | 99 | 85 | 75 | 67 | 80 | 05 | 57 | 05 | 71 | 70 |
| 96 | 53 | 99 | 25 | 13 | 63 |
Для компенсации влияния случайных погрешностей каждый опыт рекомендуется повторить п раз.
План эксперимента, предусматривающий реализацию половины опытов полного факторного эксперимента, называют полурепликой.
При увеличении числа факторов (k>3) возможно применение реплик большей дробности.
Дробной репликой называют план эксперимента, являющийся частью плана полного факторного эксперимента.
Дробные реплики обозначают выражением 2 k -р , где р – число линейных эффектов, приравненных к эффектам взаимодействия. При р = 1 получают полуреплику; при р = 2 получают 1/4 – реплику; при р = 3 получают 1/8 – реплику и т. д. по степеням двойки. Так, например, если в полном факторном эксперименте 23 (табл. 2.15) один из эффектов взаимодействия (Х1Х2, Х1ХЗ, Х2ХЗ, Х1Х2ХЗ) заменим четвертым фактором Х4 то получим полуреплику 24-1 от полно го факторного эксперимента 24.
Если два эффекта взаимодействия заменить факторами Х4 и Х5, то получим 1/4 – реплику 25-2 от полного факторного эксперимента 25. Можно получить 1/8 – реплику от полного факторного эксперимента, заменив три эффекта взаимодействия факторами Х4, Х5 и Х6.
Таблица 2.15
Матрица полного факторного эксперимента типа 23
| Номер опыта | X 0 | X 1 | Х2 | Х3 | X 1 Х2 | X 1 Х3 | X 2 Х3 | X 1 Х2 Х3 | Yi |
| 1 | + | – | – | + | + | – | – | + | Y 1 |
| 2 | + | + | – | + | – | + | – | – | Y2 |
| 3 | + | – | + | + | – | – | + | – | Y3 |
| 4 | + | + | + | + | + | + | + | + | Y4 |
| 5 | + | – | – | – | + | + | + | – | Y 5 |
| 6 | + | + | – | – | – | – | + | + | Y 6 |
| 7 | + | – | + | – | – | + | – | + | Y 7 |
| 8 | + | + | + | – | + | – | – | – | Y 8 |
Если заменить четыре эффекта взаимодействия факторами Х4, Х5 и Х6 и Х7, то получим 1/16 – реплику 27-4 от полного факторного эксперимента 27. Реплики, которые используют для сокращения числа опытов в 2m раз, где т = 1, 2, 3, ..., называют регулярными. В связи с тем, что в дробных репликах часть взаимодействий заменена новыми факторами, найденные коэффициенты уравнения регрессии будут являться совместными оценками линейных эффектов и эффектов взаимодействия. Коэффициенты 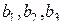 будут оценками совмещенных эффектов, а именно
будут оценками совмещенных эффектов, а именно
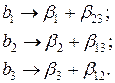
Коэффициент b 1 является оценкой влияния фактора X 1 и парного взаимодействия X 2 X 3 на функцию отклика. Влияние фактора X 1 в этом случае характеризуется величиной 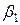 , а влияние взаимодействия – величиной
, а влияние взаимодействия – величиной 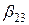 . Оценки, в которых невозможно разделить линейный эффект и эффект взаимодействия, называют смешанными. Линейные эффекты рекомендуется смешивать, прежде всего, с их взаимодействиями, которые согласно априорной информации незначимы.
. Оценки, в которых невозможно разделить линейный эффект и эффект взаимодействия, называют смешанными. Линейные эффекты рекомендуется смешивать, прежде всего, с их взаимодействиями, которые согласно априорной информации незначимы.
Число смешанных линейных эффектов в дробной реплике называют ее разрешающей способностью[2]. Часто приходится решать задачи, в которых заранее можно полагать, что эффекты взаимодействия, хотя и малы по сравнению с линейными, но все же не равны нулю. В таких случаях необходимо заранее определить, какие коэффициенты являются смешанными оценками. Тогда в зависимости от условий поставленной задачи, подбирается такая дробная реплика, с помощью которой можно извлечь максимальную информацию из эксперимента. Прямая оценка разрешающей способности дробной реплики затруднена. Поэтому дробные реплики задают с помощью генерирующих соотношений. Генерирующим называют соотношение, которое показывает, какое из взаимодействий принято незначимым и заменено новым фактором. План типа 23-1 может быть представлен двумя полурепликами (табл. 3), которые задаются одним из следующих генерирующих соотношений:
 . (2.32)
. (2.32)
Генерирующие соотношения умножим на новую независимую переменную х3:
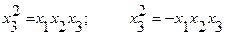 . (2.33)
. (2.33)
Таблица 2.16
Две полуреплики 23-1
| Номер опыта | X 3 = X 1 X 2 | Номер опыта | X 3 = – X 1 X 2 | ||||
| X 1 | X 2 | Х3 | X 1 | X 2 | Х3 | ||
| 1 | – | + | – | 1 | – | + | + |
| 2 | + | + | + | 2 | + | + | – |
| 3 | – | – | + | 3 | – | – | – |
| 4 | + | – | – | 4 | + | – | + |
Поскольку всегда 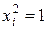 , то получим следующие выражения:
, то получим следующие выражения:
 (2.34)
(2.34)
В результате умножения генерирующего соотношения на новую переменную получают так называемый определяющий контраст. Для указанных выше полуреплик определяющими контрастами будут выражения (2.34). Зная определяющий контраст, можно найти соотношения, задающие совместные оценки. Для этого необходимо помножить независимые переменные х1, х2 и х3 на определяющий контраст.
Умножая определяющие контрасты (2.34) на х1; получим соотношения

Умножая определяющие контрасты на х2 и х3, получаем следующие соотношения


Это означает, что коэффициенты регрессии будут оценками
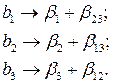
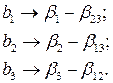
Определяющим контрастом полуреплики является соотношение
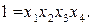
Совместные оценки будут определяться следующим образом:
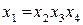

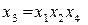
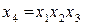
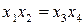
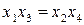
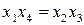
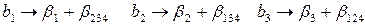
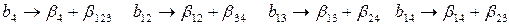 .
.
Таблица 2.17
Полуреплика 24-1 с определяющим контрастом 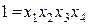
| Номер опыта | X 0 | X 1 | Х2 | Х3 | X 4 | Y |
| 1 | + | – | – | + | + | Y 1 |
| 2 | + | + | – | + | – | Y2 |
| 3 | + | – | + | + | – | Y3 |
| 4 | + | + | + | + | + | Y4 |
| 5 | + | – | – | – | + | Y 5 |
| 6 | + | + | – | – | – | Y 6 |
| 7 | + | – | + | – | – | Y 7 |
| 8 | + | + | + | – | + | Y 8 |
Таблица 2.18
Полуреплика 24-1 с определяющим контрастом 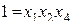
| Номер опыта | X 0 | X 1 | Х2 | Х3 | X 4 | Y |
| 1 | + | – | – | + | + | Y 1 |
| 2 | + | + | – | + | – | Y2 |
| 3 | + | – | + | + | – | Y3 |
| 4 | + | + | + | + | + | Y4 |
Окончание таблицы 2.18
| 5 | + | – | – | – | + | Y 5 |
| 6 | + | + | – | – | – | Y 6 |
| 7 | + | – | + | – | – | Y 7 |
| 8 | + | + | + | – | + | Y 8 |
Полуреплика 24-1 может быть также задана генерирующим соотношением X 4= X 1 Х2. Матрица планирования этой полуреплики представлена в табл. (2.18).
Определяющим контрастом полуреплики является соотношение
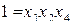
Совместные оценки в этом случае будут следующие:
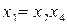
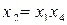
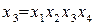
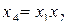
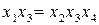
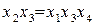
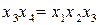

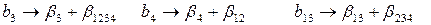
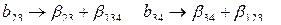
В практических задачах тройные и более высокого порядка взаимодействия значительно чаще, чем двойные, бывают равны нулю, и ими обычно можно пренебречь .
Полуреплика 24-1, заданная генерирующим соотношением 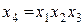 , позволяет получить раздельные оценки четырех линейных эффектов и три совместные оценки парных взаимодействий. В этом случае раздельными оценками будут
, позволяет получить раздельные оценки четырех линейных эффектов и три совместные оценки парных взаимодействий. В этом случае раздельными оценками будут 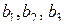 и
и 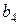 так как тройными взаимодействиями, вследствие их незначимости, можно пренебречь. В полуреплике, заданной генерирующим соотношением
так как тройными взаимодействиями, вследствие их незначимости, можно пренебречь. В полуреплике, заданной генерирующим соотношением 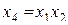 , три линейных эффекта, а именно
, три линейных эффекта, а именно 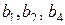 – оказались смешанными с парными взаимодействиями.
– оказались смешанными с парными взаимодействиями.
Разрешающая способность полуреплики, заданной генерирующим соотношением 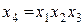 получилась значительно выше, чем у полуреплики, заданной генерирующим соотношением
получилась значительно выше, чем у полуреплики, заданной генерирующим соотношением 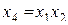 . Следовательно, разрешающая способность полуреплики зависит от генерирующего соотношения, которым она задана. Таким образом, получили весьма сложную систему смешивания.
. Следовательно, разрешающая способность полуреплики зависит от генерирующего соотношения, которым она задана. Таким образом, получили весьма сложную систему смешивания.
Все линейные эффекты оказались смешанными с несколькими парными взаимодействиями, поэтому разрешающая способность дробной реплики очень низкая. Пользоваться такой репликой можно лишь в том случае, если все парные взаимодействия близки к нулю.
Выбор дробной реплики зависит от конкретной задачи. Для получения линейной модели рекомендуют выбирать дробные реплики с возможно большей разрешающей способностью, т. е. реплики, у которых линейные эффекты смешаны с эффектами взаимодействия, близкими к нулю.
При выборе дробной реплики важно учитывать насыщенность плана, т. е. соотношение между числом опытов и числом коэффициентов, определяемых по результатам этих опытов.
Дробная реплика, полученная заменой всех эффектов взаимодействия новыми факторами, называется насыщенной. Применение насыщенных планов требует минимального числа опытов.
Число опытов в матрице насыщенной дробной реплики равно числу коэффициентов линейной модели.
Дробные реплики широко применяют при получении линейных моделей.
Эффективность применения дробных реплик зависит от удачного выбора системы смешивания линейных эффектов с эффектами взаимодействия.
При построении дробных реплик используют следующее правило: новый фактор, введенный в планирование, нужно поместить в столбец матрицы, принадлежащий взаимодействию, которым можно пренебречь.
Планирование и реализация многофакторного эксперимента второго порядка.
3.1 Центральные композиционные планы
В процессе реализации центрального композиционного ортогонального плана функцию отклика в области оптимума обычно удается аппроксимировать полиномом второй степени вида
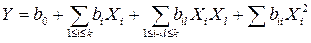 .
.
Для оценки всех коэффициентов полинома второй степени необходимо, чтобы в плане эксперимента каждый фактор принимал не менее трех значений. Применение планов типа 3k связано с большим числом опытов. Более рациональным является центральное композиционное планирование.
Центральный композиционный план второго порядка получают достройкой некоторого количества точек к «ядру», образованному линейным планом. При числе k факторов менее пяти за «ядро» центрального композиционного плана обычно принимают план полного факторного эксперимента типа 2 k .
Если число факторов более пяти, то за «ядро» центрального композиционного плана принимают полуреплику от полного факторного эксперимента.
Такой выбор «ядра» центрального композиционного плана обусловлен тем, что от «ядра» плана требуется раздельная оценка всех линейных эффектов и парных эффектов взаимодействия.
Для двух факторов центральный композиционный план второго порядка может быть представлен следующей схемой (рис. 3.1). К полному факторному эксперименту 22 (точки 1, 2, 3, 4) добавляют некоторое число n 0 опытов в центре плана (точка 9) и четыре «звездных» точки 5, 6,7,8 с координатами ( + 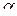 ; 0); (–
; 0); (– 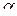 ; 0); (0, +
; 0); (0, + 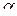 ); (0;–
); (0;– 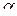 ).
).
План второго порядка для двух факторов может быть представлен матрицей (табл.3.1).
Чтобы получить центральный композиционный план второго порядка для трех факторов, к полному факторному эксперименту 23 добавляют шесть «звездных» точек с координатами ( + 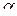 ; 0; 0); (–
; 0; 0); (– 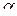 ; 0; 0); (0; +
; 0; 0); (0; + 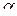 ; 0); (0; –
; 0); (0; – 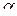 ; 0); (0; 0; +
; 0); (0; 0; + 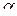 ); (0; 0; –
); (0; 0; – 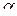 ) и некоторое число n0 точек в центре плана.
) и некоторое число n0 точек в центре плана.
Центральный композиционный план второго порядка для трех факторов может быть выражен матрицей (табл. 3.2).
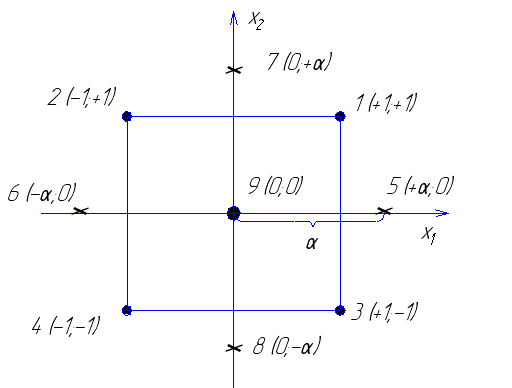
Рис. 3.1. Схема центрального композиционного плана второго порядка
для двух факторов
Таблица 3.1
Матрица центрального композиционного плана второго порядка для двух факторов
| Содержание плана | Номер опыта | x 0 | x 1 | x 2 | x 1 x 2 | x 1 2 | x 2 2 | y |
| План Типа 22 | 1 | + | + | + | + | + | + | y 1 |
| 2 | + | – | + | – | + | + | y2 | |
| 3 | + | + | – | – | + | + | y3 | |
| 4 | + | – | – | + | + | + | y4 | |
| «Звездные» точки | 5 | + | 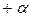
| 0 | 0 | 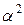
| 0 | y 5 |
| 6 | + | 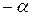
| 0 | 0 | 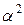
| 0 | y 6 | |
| 7 | + | 0 | 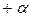
| 0 | 0 | 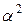
| y 7 | |
| 8 | + | 0 | 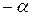
| 0 | 0 | 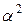
| y 8 | |
| Нулевая точка | 9 | + | 0 | 0 | 0 | 0 | 0 | y9 |
Общее число N опытов центрального композиционного плана; зависит от числа k факторов и определяется по выражению 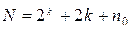 .
.
Величину «звездного» плеча 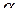 и число опытов n0 в центре плана выбирают в зависимости от принятого критерия оптимальности. За критерий оптимальности обычно принимают ортогональность или ротатабельность плана.
и число опытов n0 в центре плана выбирают в зависимости от принятого критерия оптимальности. За критерий оптимальности обычно принимают ортогональность или ротатабельность плана.
Таблица 3.2
Матрица центрального композиционного плана второго порядка для трех факторов
| Содержание плана | Номер опыта | x 0 | x 1 | x 2 | x 3 | x 1 x 2 | x 1 x 3 | x 2 x 3 | x1 2 | x 2 2 | x3 2 | y | ||
| План Типа 23 | 1 | + | + | + | + | + | + | + | + | + | + | y 1 | ||
| 2 | + | - | + | + | - | - | + | + | + | + | y2 | |||
Окончание таблицы 3.2
|
| 3 | ++ | ++ | –– | ++ | – | + | – | ++ | ++ | У+ | Y у 3 |
| 4 | ++ | –– | –– | ++ | + | – | – | ++ | ++ | ++ | y у 4 | |
| 5 | ++ | ++ | ++ | –– | + | – | – | ++ | ++ | ++ | y у5 | |
| 6 | ++ | –– | –+ | –– | – | + | – | ++ | ++ | ++ | y у6 | |
| 7 | ++ | –+ | –– | –– | – | – | + | ++ | ++ | ++ | Y у7 | |
| 8 | ++ | +– | +– | +– | + | + | + | ++ | ++ | ++ | y у8 | |
| «Звездные» точки
| 9 | ++ | 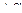 +α +α
| 00 | 00 | 0 | 0 | 0 | 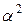 α² α²
| 00 | 00 | y у 9 |
| 10 | ++ | 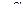 -α -α
| 00 | 00 | 0 | 0 | 0 | 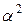 α² α²
| 00 | 00 | y у10 | |
| 11 | ++ | 00 | 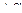 +α +α
| 00 | 0 | 0 | 0 | 00 | 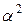 α² α²
| 00 | y у11 | |
| 12 | ++ | 00 | 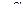 -α -α
| 00 | 0 | 0 | 0 | 00 | 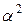 α² α²
| 00 | y у12 | |
| 13 | ++ | 00 | 00 | 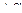 +α +α
| 0 | 0 | 0 | 00 | 00 | 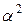 α² α²
| y у13 | |
| 14 | ++ | 00 | 00 | 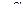 -α -α
| 0 | 0 | 0 | 00 | 00 | 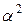 α² α²
| y у14 | |
| Нулевая точка | 15 | ++ | 00 | 00 | 00 | 0 | 0 | 0 | 00 | 00 | 00 | y у15 |
3.2. Ортогональные планы
Преимущество ортогональных планов состоит в малом объеме вычислений, тан как все коэффициенты регрессии определяются независимо друг от друга.
В ортогональных планах сумма построчных произведений элементов двух любых столбцов матрицы планирования равна нулю.
В матрице центрального композиционного плана не все столбцы ортогональны, так как
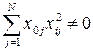 (3.2)
(3.2)
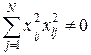 (3.3)
(3.3)
x0 всегда равно +1, а 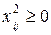 .
.

Рис. 3.2 Схема центрального композиционного плана второго порядка для трех факторов.
Например, матрица, представленная в табл 3.1, не ортогональна, ибо

Для ортогонализации соотношения (3.2) необходимо преобразовать столбцы матрицы, заменив  новой переменной
новой переменной 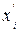 . Новую переменную находят по выражению
. Новую переменную находят по выражению
 . (3.3)
. (3.3)
После замены 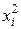 на
на 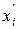 будут равны нулю суммы построчных произведений столбцов:
будут равны нулю суммы построчных произведений столбцов:
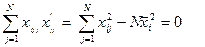 . (3.4)
. (3.4)
Так, например, в матрице центрального композиционного плана для двух факторов (табл. 3.1) получаем новые переменные
 . (3.5)
. (3.5)
Тогда
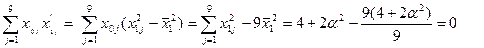 .
.
Аналогично
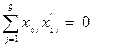 .
.
Ортогонализация соотношения (3.3) достигается выбором «звездного» плеча 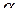 . Значения «звездного» плеча, вычисленные для различного числа факторов, приведены в табл. 3.3.
. Значения «звездного» плеча, вычисленные для различного числа факторов, приведены в табл. 3.3.
Если ортогональность принять за достаточный критерий оптимальности плана эксперимента, то на число опытов в центре плана не накладывается какого-либо ограничения, и обычно n 0 = 1.
Таблица 3.3
Величина «звездного» плеча 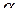
| Число независимых переменных | Ядро плана | Число дополнительных опытов | Величина плеча 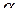
|
| 2 | 22 | 5 | 1,000 |
| 3 | 23 | 7 | 1,215 |
| 4 | 24 | 9 | 1,414 |
| 5 | 25-1 | 11 | 1,547 |
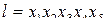
Подставляя 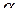 =1 в соотношения (3.5), находим новые переменные
=1 в соотношения (3.5), находим новые переменные 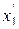 и
и 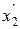
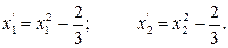
Тогда ортогональный центральный композиционный план второго порядка для двух факторов может быть представлен матрицей (табл. 3.4)
При трех факторах 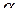 = 1,215.
= 1,215.
Используя соотношение (3.3) и матрицу плана второго порядка для трех факторов (табл3.2) находим новые переменные 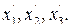
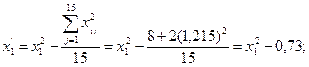
Аналогично
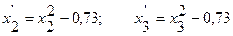 .
.
Таблица 3.4
Ортогональный центральный композиционный план второго порядка для двух факторов
| Содержание плана | Номер операции | x 0 | x 1 | x 2 | x 1 x 2 | x 1 2 -2/3 | x 2 2 -2/3 | y |
| План типа 22 | 1 | + | + | + | + | + 1/3 | + 1/3 | y 1 |
| 2 | + | – | + | – | + 1/3 | + 1/3 | y2 | |
| 3 | + | + | – | – | + 1/3 | + 1/3 | y3 | |
| 4 | + | – | – | + | + 1/3 | + 1/3 | y4 | |
| «Звездные» точки с плечом | 5 | + | + | 0 | 0 | + 1/3 | – 2/3 | y 5 |
| 6 | + | – | 0 | 0 | + 1/3 | – 2/3 | y 6 | |
| 7 | + | 0 | + | 0 | – 2/3 | + 1/3 | y 7 | |
| 8 | + | 0 | – | 0 | – 2/3 | + 1/3 | y 8 | |
| Нулевая точка | 9 | + | 0 | 0 | 0 | – 2/3 | – 2/3 | y9 |
Матрица ортогонального планирования для трех факторов представлена в таблице 3.5. Благодаря ортогональности матрицы планирования коэффициенты регрессии определяются независимо друг от друга по формуле
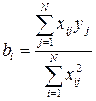 ;
;
где i – номер столбца матрицы;
j – номер опыта;
xij – элементы соответствующего столбца матрицы;
yi – значение параметра оптимизации в i-м опыте.
Дисперсии коэффициентов регрессии определяются по формуле
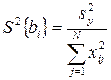 .
.
Дисперсии коэффициентов не равны, так как суммы квадратов элементов столбцов матрицы 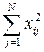 не равны друг другу.
не равны друг другу.
Реализация опытов по матрице планирования с квадратичной переменной позволяет построить модель вида:

Неизвестный коэффициент b 0 находят по выражению
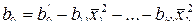
с дисперсией
 .
.
Таблица 3.5
Матрица центрального композиционного плана второго порядка
для трех факторов
| Содержание плана | № Опыта | x х0 | x х1 | x х2 | x х3 | x х1 x 2 | x х1 x 3 | x х2 x 3 | x 1 2 -0,73 | x 2 2 -0,73 | x 3 2 -0,73 | y |
| План 2³ | 1 | + | + | + | + | + | + | + | +0,27 | +0,27 | +0,27 | y 1 |
| 2 | + | – | + | + | – | + | – | +0,27 | +0,27 | +0,27 | y2 | |
| 3 | + | + | – | + | – | – | + | +0,27 | +0,27 | +0,27 | y3 | |
| 04 | –+ | – | – | + | + | – | – | +0,27 | +0,27 | +0,27 | y4 | |
| 05 | –+ | + | + | – | + | – | – | +0,27 | +0,27 | +0,27 | y 5 | |
| 06 | –+ | – | + | – | – | + | – | +0,27 | +0,27 | +0,27 | y 6 | |
| 07 | –+ | + | – | – | – | – | + | +0,27 | +0,27 | +0,27 | y 7 | |
| 8 | + | – | – | – | + | + | + | +0,27 | +0,27 | +0,27 | y 8 | |
| Окончание таблицы 3.5 | ||||||||||||
|
«Звездные» точки с | 09 | –+ | +1,215 | 0 | 0 | 0 | 0 | 0 | +0,746 | – 0,73 | – 0,73 | y9 |
| 110 | + | –1,215 | 0 | 0 | 0 | 0 | 0 | +0,746 | – 0,73 | – 0,73 | y 10 | |
| 111 | + | 0 | +1,215 | 0 | 0 | 0 | 0 | – 0,73 | +0,746 | – 0,73 | y 11 | |
| 112 | + | 0 | –1,215 | 0 | 0 | 0 | 0 | – 0,73 | +0,746 | – 0,73 | y 12 | |
| 113 | + | 0 | 0 | +1,215 | 0 | 0 | 0 | – 0,73 | – 0,73 | +0,746 | y 13 | |
| 114 | + | 0 | 0 | –1,215 | 0 | 0 | 0 | – 0,73 | – 0,73 | +0,746 | y 14 | |
| Нулевая точка | 115 | + | 0 | 0 | 0 | 0 | 0 | 0 | – 0,73 | – 0,73 | – 0,73 | y 15 |
Проверка адекватности уравнения второго порядка, получаемого после центрального композиционного ортогонального планирования, производится так же, как и проверка адекватности линейной модели, полученной при реализации плана первого порядка.
3.3 Ротатабельное планирование
Критерий ортогональности не является достаточно сильным критерием оптимизации центрального композиционного плана второго порядка.
Информация о поверхности отклика, полученная при ортогональном планировании второго порядка, различна в разных направлениях. В то же время исследователь, начиная эксперимент, чаще всего не знает, какое направление будет представлять преимущественный интерес.
В тех случаях, когда нет достоверной информации об ориентации поверхности отклика, наиболее разумным является использование центральных композиционных планов, отвечающих требованию рототабельности, т. е. планов, позволяющих получать модель, способную предсказывать значение параметра оптимизации с одинаковой точностью независимо от направления на равных расстояниях от центра плана.
Ротатабельность центрального композиционного плана достигается выбором величины «звездного» плеча 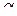 . Величину звездного плеча для «ядра», содержащего полный факторный эксперимент, определяют из соотношения
. Величину звездного плеча для «ядра», содержащего полный факторный эксперимент, определяют из соотношения
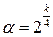 , (3.6)
, (3.6)
а для «ядра», содержащего дробную реплику,
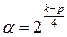 . (3.7)
. (3.7)
Для ротатабельного планирования второго порядка важное значение имеет выбор числа опытов в центре плана, так как число опытов в центре плана определяет характер распределения получаемой информации о поверхности отклика.
Число опытов в центре плана выбирается таким, чтобы обеспечивалось так называемое униформ-планирование.
Планирование называется униформ-ротатабельным, если получаемая информация постоянно остается внутри интервала 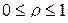 , где
, где 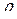 – радиус информационного контура.
– радиус информационного контура.
Униформ-ротатабельное планирование возможно, если некоторая константа 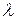 не превышает единицы (немного меньше ее):
не превышает единицы (немного меньше ее):
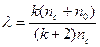 , (3.8)
, (3.8)
где
n 0 – число опытов в центре плана(число нулевых точек);
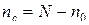 ;
;
N – общее число опытов;
k – число факторов.
Все данные, необходимые для построения матриц центрального композиционного ротатабельного планирования второго порядка при числе факторов от двух до семи, табулированы (таблица 3.6).
Матрица ротатабельного униформ - планирования второго порядка для k = 2 приведена в табл. 3.7.
Матрицы ротатабельного планирования второго порядка не ортогональны, поэтому объем вычислительной работы при определении коэффициентов регрессии довольно велик.
Таблица 3.6
Данные для построения матриц центрального композиционного ротатабельного
планирования второго порядка
| Число факторов k | «Ядро» плана | Число точек «ядра» n я | Число
«звездных»
точек 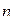
| Число
нулевых
точек 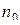
| Величина
«звездного»
плеча 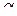
| Общее число опытов N |
| 2 | 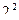
| 4 | 4 | 5 | 1,414 | 13 |
| 3 | 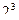
| 8 | 6 | 6 | 1,682 | 20 |
| 4 | 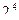
| 16 | 8 | 7 | 2,000 | 31 |
| 5 | 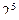
| 32 | 10 | 10 | 2,378 | 52 |
| 5 | 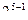
| 16 | 10 | б | 2,000 | 32 |
| 6 | 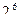
| 64 | 12 | 15 | 2,828 | 91 |
| 6 | 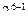
| 32 | 12 | 9 | 2,378 | 53 |
| 7 | 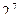
| 128 | 14 | 21 | 3,363 | 163 |
| 7 | 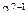
| 64 | 14 | 14 | 2,828 | 92 |
Вычисление коэффициентов регрессии рекомендуется проводить с помощью электронных вычислительных машин, используя метод наименьших квадратов.
Коэффициенты уравнения регрессии определяют по формулам:
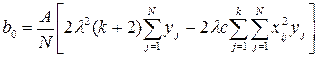 ; (3.9)
; (3.9)
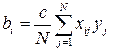 ; (3.10)
; (3.10)
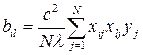 ; (3.11)
; (3.11)
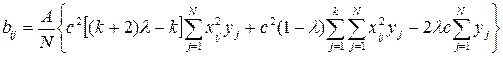 . (3.12)
. (3.12)
Таблица 3.7
Матрица ротатабельного униформ - планирования для k = 2
| № Опыта | x х0 | x 1 | x 2 | х1 х2 | 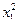 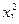
|
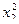
| y | № Опыта | x0 | x1 | x2 | х1 х2 |  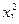
|
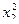
| y |
| 1 | + | + | + | + | + | + | y1 | 8 | + | 0 | –1,414 | 0 | 0 | 2 | y8 |
| 2 | + | – | + | – | + | + | y2 | 9 | + | 0 | 0 | 0 | 0 | 0 | y9 |
| 3 | + | + | – | – | + | + | y3 | 10 | + | 0 | 0 | 0 | 0 | 0 | y10 |
| 4 | + | – | – | + | + | + | y4 | 11 | + | 0 | 0 | 0 | 0 | 0 | y11 |
| 5 | + | +1,414 | 0 | 0 | 2 | 0 | y5 | 12 | + | 0 | 0 | 0 | 0 | 0 | y12 |
| 6 | + | –1,414 | 0 | 0 | 2 | 0 | y6 | 13 | + | 0 | 0 | 0 | 0 | 0 | y13 |
| 7 | + | 0 | +1.414 | 0 | 0 | 2 | y7 |
где
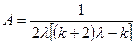 ;
; 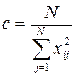 .
.
Дисперсии коэффициентов уравнения регрессии находят по формулам
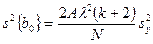 ; (3.13)
; (3.13)
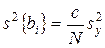 ; (3.14)
; (3.14)
 ; (3.15)
; (3.15)
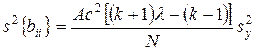 . (3.16)
. (3.16)
Вычислив коэффициенты уравнения регрессии, определяют их доверительные интервалы. После этого, исключив из уравнения статистически незначимые коэффициенты, получают математическую модель. Адекватность полученной модели проверяют с помощью расчетного критерия Фишера
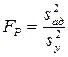 .
.
Дисперсию параметра оптимизации определяют по результатам опытов в центре плана:
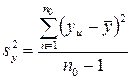 ,
,
где п0 – число параллельных опытов в центре плана; уи – значение параметра оптимизации в и-м опыте; 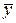 – среднее арифметическое значение параметра оптимизации в п0 опытах; и – номер параллельного опыта в центре плана.
– среднее арифметическое значение параметра оптимизации в п0 опытах; и – номер параллельного опыта в центре плана.
Для определения 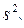 вычисляют сумму sR квадратов отклонений расчетных
вычисляют сумму sR квадратов отклонений расчетных 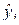 значений функции отклика от экспериментальных
значений функции отклика от экспериментальных 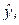 :
:
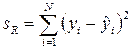 .
.
Из полученной суммы sR вычитают сумму sE, использованную для определения дисперсии параметра оптимизации по результатам опытов в центре плана:
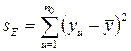 . (3.17)
. (3.17)
Полученный результат (s R – sE) делят на число степеней свободы 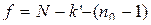 , где к' – число статистически значимых коэффициентов регрессии. Таким образом,
, где к' – число статистически значимых коэффициентов регрессии. Таким образом,
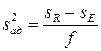 . (3.18)
. (3.18)
Если FP<FT (при выбранном уровне значимости), то гипотеза адекватности модели принимается. Если гипотеза адекватности модели не принимается, то применяют планирование третьего порядка или повторяют все опыты, сузив интервалы варьирования или изменив основные уровни факторов.
ПРИЛОЖЕНИЕ. Таблицы математической статистики.
Таблица 1
Значения t – критерия Стьюдента
(q – уровень значимости; f – число степеней свободы).
| f | q | f | q | f | q | |||
| 0,05 | 0,01 | 0,05 | 0,01 | 0,05 | 0,01 | |||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | 12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 2,23 2,20 2,18 2,16 | 63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 3,17 3,11 3,05 3,01 | 14 15 16 17 18 19 20 21 22 23 24 25 26 | 2,14 2,13 2,12 2,11 2,10 2,09 2,09 2,08 2,07 2,07 2,06 2,06 2,06 | 2,98 2,95 2,92 2,90 2,88 2,86 2,85 2,83 2,82 2,81 2,80 2,79 2,78 | 27 28 29 30 40 50 60 80 100 120 200 500 ∞ | 2,05 2,05 2,05 2,04 2,02 2,01 2,00 1,99 1,98 1,98 1,97 1,96 1,96 | 2,77 2,76 2,76 2,75 2,70 2,68 2,66 2,64 2,63 2,62 2,60 2,59 2,58 |
Таблица 2
Значения F- критерия Фишера.
(f1- число степеней свободы большой дисперсии; f2-число степеней свободы меньшей дисперсии).
| f2 | f1 | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 30 | ∞ | |
| q=0,05 | |||||||||||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 | 161 18,51 10,13 7,71 6,61 5,59 5,59 5,32 5,12 4,96 4,84 4,75 4,67 4,60 4,54 4,49 4,45 4,41 4,38 4,35 4,32 4,30 4,28 4,26 | 200 19,00 9,55 6,94 5,79 5,14 4,74 4,46 4,26 4,10 3,98 3,89 3,81 3,74 3,68 3,63 3,59 3,55 3,52 3,49 3,47 3,44 3,42 3,40 | 216 19,16 9,28 6,59 5,41 4,76 4,35 4,07 3,86 3,71 3,59 3,49 3,41 3,34 3,29 3,24 3,20 3,16 3,13 3,10 3,07 3,05 3,03 3,01 | 225 19,25 9,12 6,39 5,19 4,53 4,12 3,84 3,63 3,48 3,36 3,26 3,18 3,11 3,06 3,01 2,96 2,93 2,90 2,87 2,84 2,82 2,80 2,78 | 230 19,30 9,01 6,26 5,05 4,39 3,97 3,69 3,48 3,33 3,20 3,11 3,03 2,96 2,90 2,85 2,81 2,77 2,74 2,71 2,68 2,66 2,64 2,62 | 234 19,33 8,94 6,16 4,95 4,28 3,78 3,58 3,37 3,22 3,09 3,00 2,92 2,85 2,79 2,74 2,70 2,66 2,63 2,60 2,57 2,55 2,53 2,51 | 237 19,35 8,89 6,09 4,88 4,21 3,79 3,50 3,29 3,14 3,01 2,91 2,83 2,76 2,71 2,66 2,61 2,58 2,54 2,51 2,49 2,46 2,44 2,42 | 239 19,37 8,85 6,04 4,82 4,15 3,73 3,44 3,23 3,07 2,95 2,85 2,77 2,70 2,64 2,59 2,55 2,51 2,48 2,45 2,42 2,40 2,37 2,36 | 241 19,38 8,81 6,00 4,77 4,10 3,68 3,39 3,18 3,02 2,90 2,80 2,71 2,65 2,59 2,54 2,49 2,46 2,42 2,39 2,37 2,34 2,32 2,25 | 242 19,40 8,79 5,94 4,74 4,06 3,64 3,35 3,14 2,98 2,85 2,75 2,67 2,60 2,54 2,49 2,45 2,41 2,38 2,35 2,32 2,30 2,27 2,25 | 244 19,41 8,74 5,91 4,68 4,00 3,57 3,28 3,07 2,91 2,79 2,69 2,60 2,53 2,48 2,42 2,38 2,34 2,31 2,28 2,25 2,23 2,20 2,18 | 246 19,43 8,70 5,86 4,62 3,94 3,51 3,22 3,01 2,85 2,72 2,62 2,53 2,46 2,40 2,35 2,31 2,27 2,23 2,20 2,18 2,15 2,13 2,11 | 248 19,45 8,66 5,80 4,56 3,87 3,44 3,15 2,94 2,77 2,65 2,54 2,46 2,39 2,33 2,28 2,23 2,19 2,16 2,12 2,10 2,07 2,05 2,03 | 250 19,46 8,62 5,75 4,50 3,81 3,38 3,08 2,86 2,70 2,57 2,47 2,38 2,31 2,25 2,19 2,15 2,11 2,07 2,04 2,01 1,98 1,96 1,94 | 254 19,50 8,53 5,63 4,36 3,67 3,23 2,93 2,71 2,54 2,40 2,30 2,21 2,13 2,07 2,01 1,96 1,92 1,88 1,84 1,81 1,78 1,76 1,73 |
Продолжение табл.2
|
f2 | f1 | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 30 | ∞ | |
| 25 26 28 29 30 40 60 120 ∞ | 4,24 4,23 4,21 4,20 4,18 4,17 4,08 4,00 3,92 3,84 | 3,39 3,37 3,35 3,34 3,33 3,32 3,23 3,15 3,07 3,00 | 2,99 2,98 2,96 2,95 2,93 2,92 2,84 2,76 2,68 2,60 | 2,76 2,74 2,73 2,71 2,70 2,69 2,61 2,53 2,45 2,37 | 2,60 2,59 2,57 2,56 2,55 2,53 2,45 2,37 2,29 2,21 | 2,49 2,47 2,46 2,45 2,43 2,42 2,34 2,25 2,17 2,10 | 2,40 2,39 2,37 2,36 2,35 2,33 2,25 2,17 2,09 2,01 | 2,34 2,32 2,31 2,29 2,28 2,27 2,18 2,10 2,02 1,94 | 2,28 2,27 2,25 2,24 2,22 2,21 2,12 2,04 1,96 1,88 | 2,24 2,22 2,20 2,19 2,18 2,16 2,08 1,99 1,91 1,83 | 2,16 2,15 2,13 2,12 2,10 2,09 2,00 1,92 1,83 1,75 | 2,09 2,07 2,06 2,04 2,03 2,01 1,92 1,84 1,75 1,67 | 2,01 1,99 1,97 1,96 1,94 1,93 1,84 1,75 1,66 1,57 | 1,92 1,90 1,88 1,87 1,85 1,84 1,74 1,65 1,55 1,46 | 1,71 169 1,67 1,65 1,64 1,62 1,51 1,39 1,25 1,00 |
| q = 0.01 | |||||||||||||||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | 4052 98,50 34,12 21,20 16,26 13,75 12,25 11,26 10,56 10,04 9,65 9,33 9,07 8,86 8,68 8,53 8,40 | 4999 99,00 30,82 18,00 13,27 10,92 9,55 8,65 8,02 7,56 7,21 6,93 6,70 6,51 6,36 6,23 6,11 | 5403 99,17 29,46 16,69 12,06 9,78 8,45 7,59 6,99 6,55 6,22 5,95 5,74 5,56 5,42 5,29 5,18 | 5625 99,25 28,71 15,98 11,39 9,15 7,85 7,01 6,42 5,99 5,67 5,41 5,21 5,04 4,89 4,77 4,67 | 5764 99,30 28,42 15,52 10,97 8,75 7,46 6,63 6,06 5,64 5,32 5,06 4,86 4,69 4,56 4,44 4,34 | 5859 99,33 27,91 15,21 10,67 8,47 7,19 6,37 5,80 5,39 5,07 4,82 4,62 4,46 4,32 4,20 4,10 | 5928 99,36 27,67 14,98 10,46 8,26 6,99 6,18 5,61 5,20 4,89 4,64 4,44 4,28 4,14 4,03 3,93 | 5982 99,37 27,49 14,80 10,29 8,10 6,84 6,03 5,47 5,06 4,74 4,50 4,30 4,14 4,00 3,89 3,79 | 6022 99,39 27,35 14,66 10,16 7,98 6,72 5,91 5,35 4,94 4,63 4,39 4,19 4,03 3,89 3,78 3,68 | 6056 99,40 27,23 14,55 10,05 7,87 6,62 5,81 5,26 4,85 4,54 4,30 4,10 3,94 3,80 3,69 3,59 | 6106 99,42 27,05 14,37 9,89 7,72 6,47 5,67 5,11 4,71 4,40 4,16 3,96 3,80 2,67 3,55 3,46 | 6157 99,43 26,87 14,20 9,72 7,56 6,31 5,52 4,96 4,56 4,25 4,01 3,82 3,66 3,52 3,41 3,31 | 6209 99,45 26,69 14,02 9,55 7,40 6,16 5,36 4,81 4,41 4,10 3,86 3,66 3,51 3,37 3,26 3,16 | 6261 99,47 26,50 13,84 9,38 7,23 5,99 5,20 4,65 4,25 3,94 3,70 3,51 3,35 3,21 3,10 3,00 | 6366 99,50 26,13 13,46 9,02 6,88 5,65 4,86 4,31 3,91 3,60 3,36 3,17 3,00 2,87 2,75 2,65 |
Окончание табл. 2
|
f2 | f1 | ||||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 12 | 15 | 20 | 30 | ∞ | |
| 18 19 20 21 24 25 26 27 28 29 30 40 60 120 ∞ | 8,29 8,18 8,10 8,02 7,82 7,77 7,72 7,68 7,64 7,60 7,56 7,31 7,08 6,85 6,63 | 6,01 5,93 5,85 5,78 5,61 5,57 5,53 5,49 5,45 5,42 5,39 5,18 4,98 4,79 4,61 | 5,09 5,01 4,94 4,87 4,72 4,68 4,64 4,60 4,57 4,54 4,51 4,31 4,13 3,95 3,78 | 4,58 4,50 4,43 4,37 4,22 4,18 4,14 4,11 4,07 4,04 4,02 3,85 3,63 3,48 3,32 | 4,25 4,17 4,10 4,04 3,90 3,85 3,82 3,78 3,75 3,73 3,70 3,51 3,34 3,17 3,02 | 4,01 3,94 3,87 3,81 3,67 3,63 3,59 3,56 3,53 3,50 3,47 3,29 3,12 2,96 2,80 | 3,84 3,77 3,70 3,64 3,50 3,46 3,42 3,39 3,36 3,33 3,30 3,12 2,95 2,79 2,64 | 3,71 3,61 3,56 3,51 3,36 3,32 3,29 3,26 3,23 3,20 3,17 2,99 2,82 2,66 2,51 | 3,60 3,52 3,46 3,40 326 3,22 3,18 3,15 3,12 3,09 3,07 2,89 2,72 2,56 2,41 | 3,51 3,43 3,37 3,31 3,17 3,13 3,09 3,06 3,03 3,00 2,98 2,80 2,63 2,47 2,32 | 3,37 3,30 3,23 3,17 3,03 2,99 2,96 2,93 2,90 2,87 2,84 2,66 2,50 2,34 2,18 | 3,23 3,15 3,09 3,03 2,89 2,85 2,81 2,78 2,75 2,73 2,70 2,52 2,35 2,19 2,04 | 3,08 3,00 2,94 2,88 2,74 2,70 2,66 2,63 2,60 2,57 2,55 2,37 2,20 2,03 1,88 | 2,92 2,84 2,78 2,72 2,58 2,54 2,50 2,47 2,44 2,41 2,39 2,20 2,03 1,86 1,70 | 2,57 2,49 2,42 2,36 2,21 2,17 2,13 2,10 2,06 2,03 2,01 1,80 1,60 1,38 1,00 |
Таблица 3
Значение G – критерия Кохрена
(f – число степеней свободы выборки; m – количество выборок)
|
m | f | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 16 | 36 | 144 | ∞ | |
| q = 0,05 | ||||||||||||||
| 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 | 0,99 0,97 0,91 0,84 0,78 0,73 0,68 0,64 0,60 0,54 0,47 0,39 0,34 0,29 0,24 0,17 0,10 | 0,98 0,87 0,77 0,68 0,62 0,56 0,52 0,48 0,45 0,39 0,33 0,27 0,24 0,20 0,16 0,11 0,06 | 0,94 0,80 0,68 0,60 0,53 0,48 0,44 0,40 0,27 0,33 0,28 0,22 0,19 0,16 0,13 0,09 0,05 | 0,91 0,75 0,63 0,54 0,48 0,43 0,39 0,36 0,33 0,29 0,24 0,19 0,17 0,14 0,11 0,09 0,04 | 0,88 0,71 0,59 0,51 0,44 0,40 0,36 0,33 0,30 0,26 0,22 0,17 0,15 0,12 0,10 0,07 0,04 | 0,85 0,68 0,56 0,48 0,42 0,37 0,34 0,31 0,28 0,24 0,20 0,16 0,14 0,11 0,09 0,06 0,03 | 0,83 0,65 0,54 0,46 0,40 0,35 0,32 0,29 0,27 0,23 0,19 0,15 0,13 0,11 0,08 0,06 0,03 | 0,82 0,63 0,52 0,44 0,38 0,34 0,30 0,28 0,25 0,22 0,18 0,14 0,12 0,10 0,08 0,06 0,03 | 0,80 0,62 0,50 0,42 0,37 0,33 0,29 0,27 0,24 0,21 0,17 0,14 0,12 0,10 0,07 0,05 0,03 | 0,79 0,60 0,49 0,41 0,36 0,32 0,28 0,26 0,24 0,20 0,17 0,13 0,11 0,09 0,07 0,05 0,03 | 0,73 0,55 0,44 0,36 0,31 0,28 0,25 0,22 0,20 0,17 0,14 0,11 0,09 0,08 0,06 0,04 0,02 | 0,66 0,47 0,37 0,31 0,26 0,23 0,20 0,18 0,17 0,14 0,11 0,09 0,07 0,06 0,05 0,03 0,02 | 0,58 0,40 0,31 0,25 0,21 0,18 0,16 0,14 0,13 0,11 0,09 0,07 0,06 0,05 0,03 0,02 0,01 | 0,50 0,33 0,25 0,20 0,17 0,14 0,13 0,11 0,10 0,08 0,07 0,05 0,04 0,03 0,03 0,02 0,01 |
Окончание табл.3
|
m | f | |||||||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 16 | 36 | 144 | ∞ | |
| q = 0,01 | ||||||||||||||
| 2 3 4 5 6 7 8 9 10 12 15 20 24 30 40 60 120 | 0,99 0,99 0,97 0,93 0,88 0,84 0,79 0,75 0,72 0,65 0,57 0,48 0,42 0,36 0,29 0,22 0,12 | 0,99 0,94 0,86 0,79 0,72 0,66 0,62 0,57 0,54 0,48 0,41 0,33 0,29 0,24 0,19 0,14 0,08 | 0,98 0,88 0,78 0,70 0,63 0,57 0,52 0,48 0,45 0,39 0,33 0,27 0,23 0,19 0,15 0,11 0,06 | 0,96 0,83 0,72 0,63 0,56 0,51 0,46 0,43 0,39 0,33 0,29 0,23 0,20 0,16 0,13 0,09 0,05 | 0,94 0,79 068 0,59 0,52 0,47 0,42 0,39 0,36 0,31 0,26 0,20 0,18 0,15 0,11 0,08 0,04 | 0,92 0,76 0,64 0,55 0,49 0,43 0,39 0,36 0,33 0,29 0,24 0,19 0,16 0,13 0,10 0,07 0,04 | 0,90 0,73 0,61 0,53 0,46 0,41 0,37 0,34 0,31 0,27 0,22 0,17 0,15 0,12 0,10 0,07 0,04 | 0,88 0,71 0,59 0,50 0,44 0,39 0,35 0,32 0,29 0,25 0,21 0,16 0,14 0,12 0,09 0,06 0,03 | 0,87 0,69 0,57 0,49 0,42 0,38 0,34 0,31 0,28 0,24 0,20 0,16 0,13 0,12 0,09 0,06 0,03 | 0,85 0,67 0,55 0,47 0,41 0,36 0,32 0,30 0,27 0,23 0,19 0,15 0,13 0,11 0,08 0,06 0,03 | 0,79 0,61 0,49 0,41 0,35 0,31 0,28 0,25 0,23 0,20 0,16 0,12 0,11 0,09 0,07 0,05 0,02 | 0,71 0,52 0,41 0,34 0,29 0,25 0,22 0,20 0,18 0,15 0,13 0,10 0,08 0,07 0,05 0,03 0,02 | 0,61 0,42 0,33 0,26 0,22 0,19 0,17 0,15 0,14 0,12 0,09 0,07 0,06 0,05 0,04 0,02 0,01 | 0,50 0,33 0,25 0,20 0,17 0,14 0,13 0,11 0,10 0,08 0,07 0,05 0,04 0,03 0,03 0,02 0,01 |
Таблица 4
Значения критерия 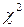 ( k – число степеней свободы)
( k – число степеней свободы)
|
k | q |
k | q |
k | q |
k | q | ||||
| 00,5 | 0,01 | 0,05 | 0,01 | 0,05 | 0,01 | 0,05 | 0,01 | ||||
| 1 2 3 4 5 6 7 8 9 10 11 12 13 | 3,84 5,99 7,81 9,49 11,1 12,6 14,1 15,5 16,9 18,3 19,7 21,0 22,4 | 6,63 9,21 11,3 13,3 15,1 16,8 18,5 20,1 21,7 23,2 24,7 26,2 27,7 | 14 15 16 17 18 19 20 21 22 23 24 25 26 | 23,7 25,0 26,3 27,6 28,9 30,1 31,4 32,7 33,9 35,2 36,4 37,7 38,9 | 29,1 30,6 32,0 33,4 34,8 36,2 37,6 38,9 40,3 41,6 43,0 44,3 45,6 | 27 28 29 30 31 32 33 34 35 36 37 38 39 | 40,1 41,3 42,6 43,8 45,0 46,2 47,4 48,6 49,8 51,0 52,2 53,4 54,6 | 47,0 48,3 49,6 50,9 52,2 53,2 54,8 56,1 57,3 58,6 59,9 61,2 62,4 | 40 41 42 43 44 45 46 47 48 49 50 | 55,8 56,9 58,1 59,3 60,5 61,7 62,8 64,0 65,2 66,3 67,5 | 63,7 65,0 66,2 67,5 68,7 70,0 71,2 72,4 73,7 74,9 76,2 |
Таблица 5
Равномерно распределенные случайные числа
| 10 | 09 | 73 | 25 | 33 | 76 | 52 | 01 | 35 | 86 | 34 | 67 | 35 | 48 | 76 | 80 | 95 | 90 | 91 | 17 |
| 37 | 54 | 20 | 48 | 05 | 64 | 89 | 47 | 42 | 96 | 24 | 80 | 52 | 40 | 37 | 20 | 63 | 61 | 04 | 02 |
| 08 | 42 | 26 | 89 | 53 | 19 | 64 | 50 | 93 | 03 | 23 | 20 | 90 | 25 | 60 | 15 | 95 | 33 | 47 | 64 |
| 99 | 01 | 90 | 25 | 29 | 09 | 37 | 67 | 07 | 15 | 38 | 31 | 13 | 11 | 65 | 88 | 67 | 67 | 43 | 97 |
| 12 | 80 | 79 | 99 | 70 | 80 | 15 | 73 | 61 | 47 | 64 | 03 | 23 | 66 | 53 | 98 | 95 | 11 | 68 | 77 |
| 66 | 06 | 57 | 47 | 17 | 34 | 07 | 27 | 68 | 50 | 36 | 69 | 73 | 61 | 70 | 65 | 81 | 33 | 98 | 85 |
| 31 | 06 | 01 | 08 | 05 | 45 | 57 | 18 | 24 | 06 | 35 | 30 | 34 | 26 | 14 | 86 | 79 | 90 | 74 | 39 |
| 85 | 26 | 97 | 76 | 02 | 02 | 05 | 16 | 56 | 92 | 68 | 66 | 57 | 48 | 18 | 73 | 05 | 38 | 52 | 47 |
| 63 | 57 | 33 | 21 | 35 | 05 | 32 | 54 | 70 | 48 | 90 | 55 | 35 | 75 | 48 | 28 | 46 | 82 | 87 | 09 |
| 73 | 79 | 64 | 57 | 53 | 03 | 52 | 96 | 47 | 78 | 35 | 80 | 83 | 42 | 82 | 60 | 93 | 52 | 03 | 44 |
| 98 | 52 | 01 | 77 | 67 | 14 | 90 | 56 | 86 | 07 | 22 | 10 | 94 | 05 | 58 | 60 | 97 | 09 | 34 | 33 |
| 11 | 80 | 50 | 54 | 31 | 39 | 80 | 82 | 77 | 32 | 50 | 72 | 56 | 82 | 48 | 29 | 40 | 52 | 42 | 01 |
| 83 | 45 | 29 | 96 | 34 | 06 | 28 | 89 | 80 | 83 | 13 | 74 | 67 | 00 | 78 | 18 | 47 | 54 | 06 | 10 |
| 88 | 68 | 54 | 02 | 00 | 86 | 50 | 75 | 84 | 01 | 36 | 76 | 66 | 79 | 51 | 90 | 36 | 47 | 64 | 93 |
| 99 | 59 | 46 | 73 | 48 | 87 | 51 | 76 | 49 | 69 | 91 | 82 | 60 | 89 | 28 | 93 | 78 | 56 | 13 | 68 |
| 65 | 48 | 11 | 76 | 74 | 17 | 46 | 85 | 09 | 50 | 58 | 04 | 77 | 69 | 74 | 73 | 03 | 95 | 71 | 86 |
| 80 | 12 | 43 | 56 | 35 | 17 | 72 | 70 | 80 | 15 | 45 | 31 | 82 | 23 | 74 | 21 | 11 | 57 | 82 | 53 |
| 74 | 35 | 09 | 98 | 17 | 77 | 40 | 27 | 72 | 14 | 43 | 23 | 60 | 02 | 10 | 45 | 52 | 16 | 42 | 37 |
| 69 | 91 | 62 | 68 | 03 | 66 | 25 | 22 | 91 | 48 | 36 | 93 | 68 | 72 | 03 | 76 | 62 | 11 | 39 | 90 |
| 09 | 89 | 32 | 05 | 05 | 14 | 22 | 56 | 85 | 14 | 46 | 42 | 75 | 67 | 88 | 96 | 29 | 77 | 88 | 22 |
СПИСОК ЛИТЕРАТУРЫ
1.Кане М. М. Исследования и изобретательство в машиностроении /И. Л. Барщай, Г. Я. Беляев, О. Г. Девойно// Под общ. ред. М. М. Кане.-Мн.: УП Технопринт, 2003.-237с, ISBN 985-464-479-0
2.Пижурин А. А., Пижурин А. А. Основы научных исследований в деревообработке. – М: МГУЛ, 2005.-ЗО6с.
З.Спиридонов А. А. Планирование эксперимента при исследовании технологических процессов.– М.: Машиностроение, 1981.- 184с., ББК 34.5 С72.
Учебное пособие
Гусев Владимир Григорьевич
Теория и практика планирования многофакторных экспериментов.
Учебное пособие по изучению курса для магистрантов и аспирантов
Редактор
Корректор
Компьютерная верстка
ЛР№…….. Подписано / печать……..
Формат 60*84/16. Бумага для множит. техники
Гарнитура Таймс
Печать на ризографе. Усл. Печ. Листов……Уч. – изд.л……Тираж……Заказ
Редакционно-издательский комплекс
Владимирского государственного университета.
600000, г. Владимир, ул. Горького, 87
Оглавление
Предисловие……………………………………………………………
1.Основные понятия и определения
1.1.Понятия и характеристика однофакторного, многофакторного
экспериментов, понятие планирования экспериментов…………………
1.2. Понятия объекта исследования, параметра оптимизации, фактора и требования, предъявляемые к ним………..…………………………………
2.Планирование и реализация полного факторного эксперимента
2.1.Выбор факторов и их кодирование……………………………………
2.2.Выбор модели……………………………………………………………
2.3.Полный факторный эксперимент………………………………………
2.4.Проведение опытов………………………………………………………
2.5.Крутое восхождение по поверхности отклика………...……………
2.6.Дробный факторный эксперимент………………………………...…
3. Планирование и реализация многофакторного эксперимента второго порядка
3.1.Центральные композиционные планы………………………...………
3.2.0ртогональные планы…………………………………………...………
3.3.Рототабельные планы……………………………………………..……
3.4.Исследование области оптимума, представленной полиномом второй степени…………………………………………………………………….
3.5.Исследование аэродинамических потоков, генерируемых дискретными шлифовальными кругами, на основе центрального композиционного планирования второго порядка……………………………
4.Применение планирования многофакторных экспериментов при механической обработке
4.1.Исследование шероховатости поверхности с использованием ротатабельного планирования…………………………………………….……..
4.2.0птимизация геометрии режущего инструмента на основе метода Бокса-Уилсона…………………………………………………………….……….
4.3.Применение ротатабельного планирования второго порядка для исследования процесса торцового фрезерования……………………………..
4.4.Составление композиционного плана проведения экспериментов при анализе параметров процесса шлифования………………………………
4.5.Исследование шероховатости поверхности, обработанной хонингованием…………………………………………………………………….
4.6.Исследование температуры, возникающей в процессе резания……
Приложение. Таблицы математической статистики…………………….
Список литературы………………………………………
ГУСЕВ В. Г.
ТЕОРИЯ И ПРАКТИКА ПЛАНИРОВАНИЯ
МНОГОФАКТОРНЫХ ЭКСПЕРИМЕНТОВ
Владимир 2010
УДК 621: 658.5.012.1
Рецензент
Заслуженный изобретатель Российской Федерации, доктор технических наук, профессор Денисенко В.И.
Печатается по решению редакционно-издательского совета Владимирского государственного университета
Гусев В.Г. Теория и практика планирования многофакторных экспериментов:
Учебное пособие. - Владимирский государственный университет:
Владимир, 2010.
Составлены в соответствии с требованиями государственного образовательного стандарта высшего профессионального образования. Изложены основные принципы и научные положения теории планирования линейных многофакторных экспериментов, экспериментов второго порядка, методология их практической реализации и статистической обработки результатов на конкретных примерах исследования процессов механической обработки изделий машиностроения.
Предназначены для магистрантов дневной формы обучения по направлению «Технология, оборудование и автоматизация машиностроительного производства», а также аспирантов, обучающихся по специальностям: 05.03.01 - «Технологии и оборудование механической и физико-технической обработки», 05.02.08 - «Технология машиностроения», а также по другим техническим специальностям. Ил. Табл.
ПРЕДИСЛОВИЕ
В ходе разработки технических устройств и систем, технологических процессов механической и физико-технической обработки, сборки и испытания его создателям приходится решать множество научно-технических задач, различных по уровню сложности и объему. При этом часто встречаются задачи, связанные с выбором наиболее правильного технического решения и нахождением оптимальных значений всех параметров и характеристик.
Сказанное в полной мере относится к исследованиям различного рода явлений, протекающих в механических и других объектах и системах.
В настоящее время большое количество молодых специалистов с высшим образованием, приходящих на работу в научно-производственные предприятия, занимающиеся созданием новой техники и технологии, недостаточно подготовлены к поиску новых технических решений и их использованию при разработке конкретной продукции.
Такая ситуация в значительной мере обусловлена недостаточным вниманием существующих государственных стандартов высшего профессионального инженерного образования к изучению современных методов научных исследований и, в частности, к теории планирования многофакторных экспериментов и оптимизации важнейших параметров проектируемой техники и технологии.
Имея достаточно хорошую компьютерную подготовку, используемую для создания технических объектов и технологических процессов, они часто не владеют методикой подготовки, проведения многофакторных экспериментов, статистической обработки результатов и оптимизации полученных математических моделей.
Отсутствие конкретных знаний и навыков в области оптимизации технических и технологических решений отражается непосредственно на научно-техническом уровне, а, следовательно, на конечных результатах исследований и разработок.
При переходе к двух-уровневой подготовке молодых специалистов с высшим образованием (бакалавров и магистров) остро встает вопрос овладения современными методами научного творчества, поиска новых решений и оптимизации моделей, описывающих изучаемые объекты, явления и процессы. Значительную роль в процессе формирования основополагающих знаний и практических навыков бакалавров и магистров в области эффективного использования научных методов исследований играет методология планирования и реализации экстремальных экспериментальных исследований. Настоящее учебное пособие направлено на теоретическую и практическую подготовку магистрантов, аспирантов в области планирования и реализации экстремальных многофакторных экспериментов, оптимизации многофакторных систем и технологических процессов механической обработки различных изделий машиностроения с наименьшими затратами.
ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
1.1 Понятия и характеристика однофакторного и многофакторного экспериментов, понятие планирования экспериментов
Для адекватного восприятия читателями излагаемого в настоящем учебном пособии материала дадим определение и понятие основных терминов и физических величин, применяемых в теории и практике планирования многофакторных экспериментов.
Эксперимент - понятие, которое произошло от латинского слова experimentum , что означает пробу, опыт. В словаре иностранных слов дано следующее определение: эксперимент - научно поставленный опыт, наблюдение в точно учитываемых условиях, позволяющих следить за ходом явления и воссоздавать его каждый раз при повторении этих условий. В энциклопедическом словаре эксперимент определен как чувственно-предметная деятельность в науке. Второе определение более широкое. Первое - более подходит к существу дисциплины "Теория планирования многофакторных экспериментов".
Эксперимент бывает однофакторный, многофакторный, физический, модельный и др. Однофакторный эксперимент - такой эксперимент, когда при изменении одной независимой переменной (фактора) и стабилизации всех остальных независимых переменных, фиксируют значения изучаемой зависимой переменной (параметра). Обработав результаты однофакторного эксперимента, находят зависимость исследуемого параметра только от одного фактора. Производя большое число однофакторных экспериментов при изучении многофакторной системы, получают частотные зависимости, представленные многими графиками, имеющими иллюстративный характер. Найденные таким образом частные зависимости невозможно объединить в одну общую модель процесса.
Использование однофакторного эксперимента для всестороннего исследования многофакторного процесса требует постановки очень большого числа опытов. Для их выполнения в ряде случаев необходимо значительное время, в течение которого влияние неконтролируемых факторов на результаты опытов может существенно измениться. Отсюда следует, что результаты однофакторных экспериментов, полученные при исследовании многофакторных систем, малопригодны для практического использования. Кроме того, при решении экстремальных задач данные значительного числа опытов однофакторного эксперимента оказываются ненужными, так как
получены они для области, далекой от оптимума.
Однофакторные эксперименты не отражают реальной картины явлений и процессов, протекающих в природе, поскольку они проводятся в искусственно созданных условиях, значительно отличающихся от условий многофакторного эксперимента. Для природы характерно изменение одновременно нескольких факторов, которые влияют на выходной параметр системы. В качестве примера может служить нагрев солнечными лучами воздушных масс, при котором одновременно с повышением температуры воздуха происходит изменение скорости и направления движения воздушных масс, изменение давления, влажности и др.
Приведенный пример свидетельствует о существовании многофакторных процессов, систем и объектов, изучение которых посредством однофакторных экспериментов не дает реальной картины их поведения, а поэтому результатами однофакторных экспериментов в подобных случаях пользоваться нельзя. Отмеченное не означает того, что от однофакторных экспериментов следует отказаться вообще.
Однофакторные эксперименты могут использоваться, например, для определения зависимости изучаемого параметра от какого-либо фактора с целью правильного выбора исходной априорной модели при изучении многофакторных процессов и явлений; при исследовании процесса, изменение которого зависит от какой-либо одной доминирующей независимой переменной в то время как влияние других независимых переменных на процесс незначительно
В машиностроении процессы механической, физико-технической обработки в подавляющем большинстве своем являются многофакторными, поэтому подготовка, реализация многофакторных экспериментов в этих условиях является особо актуальными.
Многофакторный эксперимент – такой эксперимент, при котором варьируют одновременно все независимые переменные (факторы), оказывающие влияние на процесс или систему. В результате обработки результатов опытов получают математическую модель, связывающую изучаемую зависимую переменную (параметр) одновременно со всеми независимыми факторами. Для изучения многофакторных систем наиболее целесообразным является применение статистических методов планирования многофакторных экспериментов.
Физический эксперимент – это реальный эксперимент с использованием оборудования, установок, устройств и т. д., а также с вещественными материалами. Это наиболее трудоёмкий, энергоёмкий и дорогой вид деятельности. Планирование эксперимента зарождалось и развивалось применительно к таким областям деятельности как металлургия, машиностроение, химическая, пищевая промышленность, транспорт и др.
Модельный эксперимент – это эксперимент с использованием модели, которая может быть трёх типов:
- физической, в этом случае она может отличаться от реального объекта масштабом;
- абстрактной, неформализованной на уровне логического мышления;
- формализованной математически. Чтобы получать на основе модельного эксперимента правильные сведения об объекте исследования, нужно построить достаточно точную модель. А поскольку невозможно абсолютно точное описание влияния всех возможных независимых переменных на процесс функционирования объекта исследования, то модель, а, следовательно, и объект описываются вероятностно.
Эксперимент, который ставится для решения задач оптимизации, называется экстремальным, поскольку он связан с поиском экстремума некоторой функции.
Под планированием эксперимента понимают нахождение условий проведения опытов, их количества в многофакторном эксперименте, необходимых и достаточных для установления взаимосвязи параметра с факторами с требуемой точностью. Планирование эксперимента – это новый раздел математической статистики. В нем всесторонне рассматриваются статистические методы планирования эксперимента. Эти методы позволяют во многих случаях при минимальном числе опытов получать модели многофакторных процессов.
Высокая эффективность использования статистических методов планирования эксперимента при исследовании технологических процессов объясняется тем, что многие важные их характеристики являются случайными величинами, законы распределения которых близки к нормальному закону. Характерными особенностями процесса планирования эксперимента являются стремление минимизировать число опытов; одновременное варьирование всех исследуемых факторов по специальным правилам - алгоритмам; применение математического аппарата, формализующего многие действия исследователя; выбор стратегии, позволяющей принимать обоснованные решения.
Таким образом, планирование эксперимента - это совокупность приемов, позволяющих исследователю разумно поставить эксперимент, сообразуясь с целью исследования, со стремлением получить максимальную информацию при необходимости экономить средства (при ограниченном числе опытов), а также правильно обработать и интерпретировать результаты экспериментов.
Техника планирования: на каждом шаге ставится небольшая серия опытов, в каждом из которых варьируются по определённым правилам все факторы.
Математическая обработка результатов эксперимента позволяет выработать условия проведения следующей серии опытов, направленных к достижению оптимума. В этом суть метода Бокса–Уилсона или метода крутого восхождения. Применение планирования эксперимента, несомненно, организует и оптимизирует деятельность экспериментатора.
Дата: 2018-12-28, просмотров: 1895.