Для определения абсолютных деформаций на границах силовых участков намечается несколько характерных сечений (рис.1.8).
Определение деформационных перемещений начинается от заделки (сечение Е–Е), поскольку заведомо известно перемещение этого сечения:
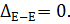
Перемещение остальных характерных сечений (м) определяется по формуле
|
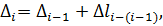
где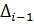 
– перемещение предыдущего характерного сечения, м;
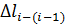– абсолютное удлинение силового участка, заключенногомежду рассматриваемыми сечениями, м.
Если продольная сила (и жесткость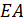 
) постоянна в пределах участка, формула определения удлинения силового участка имеет вид
|
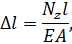
где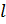 
– длина силового участка, м.
Сечение Д–Д:
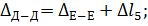
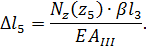
Из исходных данных
; 
;
.
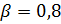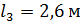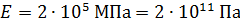Из предыдущего расчета
;
;
.
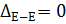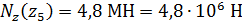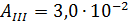Тогда
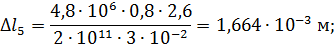
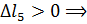
участок 5 удлиняется.
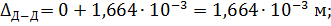
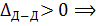
перемещение направлено от заделки (влево).
Сечение Г–Г:
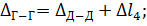
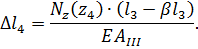
Из предыдущего расчета
;
.
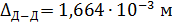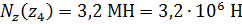Тогда
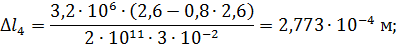
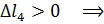
участок4 удлиняется.
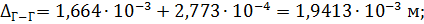
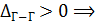
перемещение направлено от заделки (влево).
Сечение В–В:
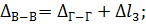
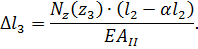
Из исходных данных
; 
;
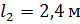Из предыдущего расчета
;
;
.
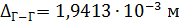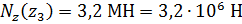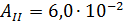Тогда
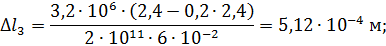
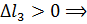
участок 3 удлиняется.
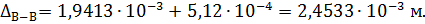
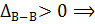
перемещение направлено от заделки (влево).
Сечение Б–Б:
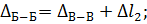
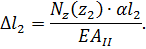
Из предыдущего расчета
;
.
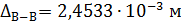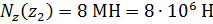Тогда
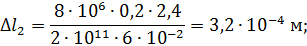
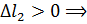
участок2 удлиняется.
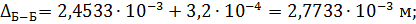
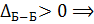
перемещение направлено от заделки (влево).
Сечение А–А:
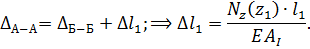
Из исходных данных
.
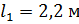Из предыдущего расчета
;
;
.
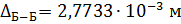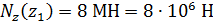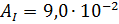Тогда
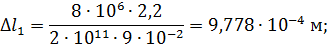
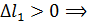
участок 1 удлиняется.
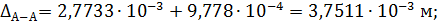
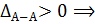
перемещение направлено от заделки (влево).
Таким образом, общее абсолютное удлинение (абсолютная деформация) стержня составляет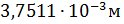 
или 3,7511 мм.
Определение относительной продольной и поперечной
деформации в заданном сечении
Относительная деформация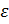 
определяется на основании закона Гука, который для случая одноосного напряженного состояния имеет вид
|
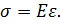
Напряжение в заданном сечении n – n(см. рис.1.8) s w:val="28"/></w:rPr><m:t>6</m:t></m:r></m:sup></m:sSup><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t> РџР°</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">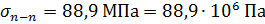 
. Модуль Юнга принимается из исходных данных
.
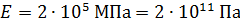Тогда
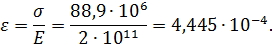
Относительная поперечная деформация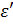 
определяется по формуле
|
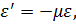
где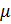 
– коэффициент Пуссона.
Из исходных данных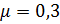 
.
Тогда
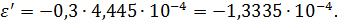
Таким образом, относительные деформации в заданном сечении определены.
Задача 1.2
Расчетная схема стержня показана на рис.1.9.
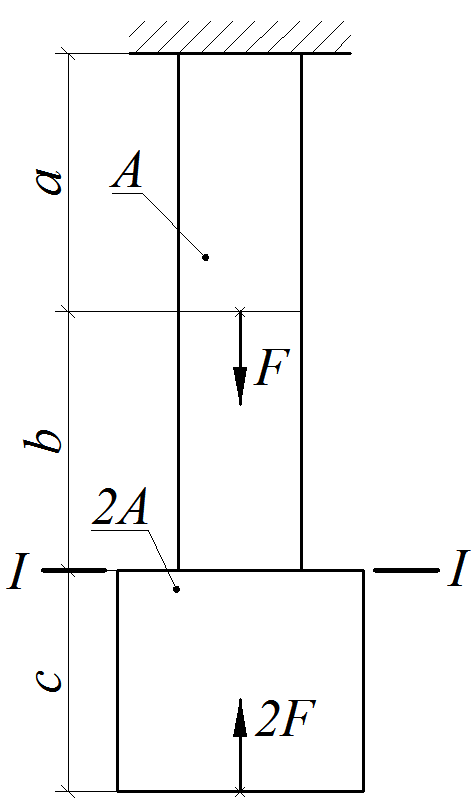
Рис. 1.9
Заданные величины:
1. Внешние силовые факторы:
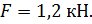
2. Площадь поперечного сечения ступеней стержня:
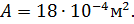
3. Длины силовых участков:
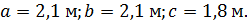
4. Модуль упругости и плотность материала:
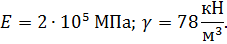
Требуется:
1. Построить эпюру продольных сил.
2. Построить эпюру нормальных напряжений.
3. Определить перемещение центра тяжести сечения I– I.
Решение
Дата: 2019-02-02, просмотров: 376.
