Раздел 1. РАСЧЕТ СТЕРЖНЕЙ ПРИ РАСТЯЖЕНИИ-СЖАТИИ
Задача 1.1
Расчетная схема стержня показана на рис.1.1.
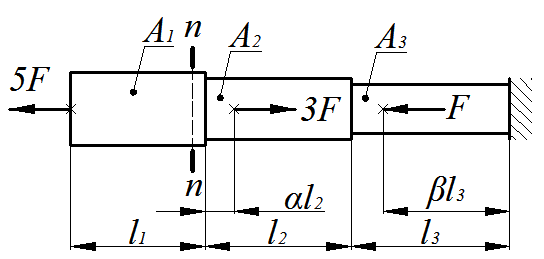
Рис.1.1
Заданные величины:
1. Внешние силовые факторы:
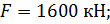
2. Площадь поперечного сечения ступеней стержня:
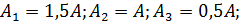
3. Длины силовых участков:
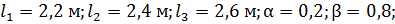
4. Характеристики прочности и упругости материала:
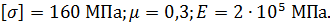
Требуется:
1. Построить эпюру продольных сил.
2. Определить площади поперечных сечений каждой ступени стержня.
3. Построить эпюру нормальных напряжений.
4. Вычислить полную абсолютную деформацию стержня.
5. Найти относительную продольную и относительную поперечную деформацию участка с заданным сечением n – n.
Решение
Построение эпюры продольных сил
Для построения эпюры продольных сил стержень разбивается на 5 силовых участков (рис.1.2). В пределах каждого силового участка производится мысленное рассечение на произвольном удалении от начала участка, и одна из частей стержня отбрасывается. В поперечном сечении оставшейся части прикладывается внутренний силовой фактор – продольная сила, выражение для которой составляется на основании условий равновесия. Чтобы не определять реакцию заделки, каждый раз рассматривается равновесие левой отсеченной части стержня.
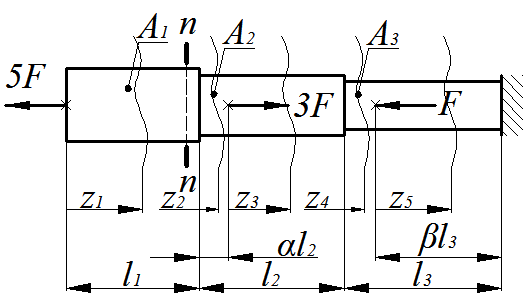
Рис.1.2
1-й силовой участок, (  ), рис. 1.3.
), рис. 1.3.
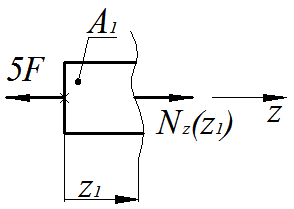
Рис.1.3
Условие равновесия отсеченной части
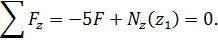
Выражение для продольной силы имеет вид
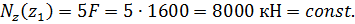
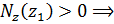
продольная сила является растягивающей.
2-й силовой участок, ( 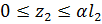 ), рис. 1.4.
), рис. 1.4.
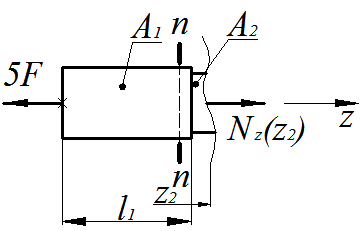
Рис.1.4
Условие равновесия отсеченной части
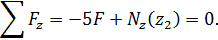
Выражение для продольной силы имеет вид
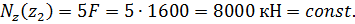
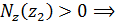
продольная сила является растягивающей.
3-й силовой участок, ( 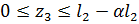 ), рис. 1.5.
), рис. 1.5.
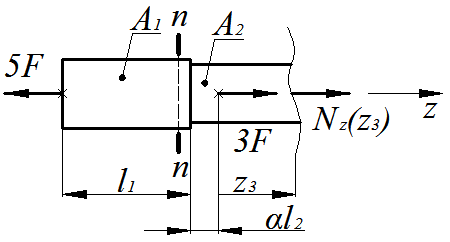
Рис.1.5
Условие равновесия отсеченной части
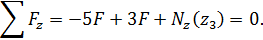
Выражение для продольной силы имеет вид
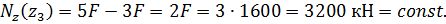
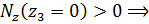
продольная сила является растягивающей.
4-й силовой участок, ( 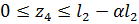 ), рис. 1.6.
), рис. 1.6.
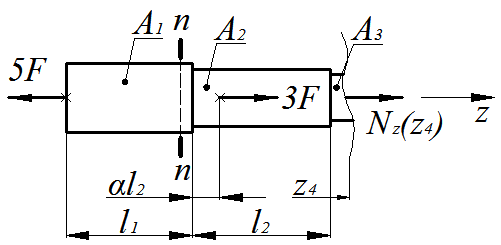
Рис.1.6
Условие равновесия отсеченной части
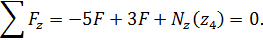
Выражение для продольной силы имеет вид
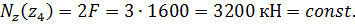
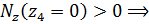
продольная сила является растягивающей.
5-й силовой участок, ( 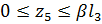 ), рис. 1.7.
), рис. 1.7.
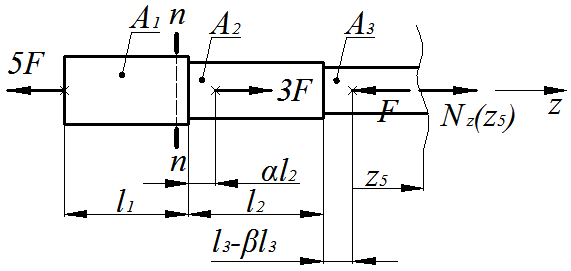
Рис.1.7
Условие равновесия отсеченной части
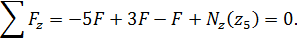
Выражение для продольной силы имеет вид
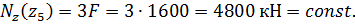
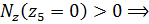
продольная сила является растягивающей.
На основании рассчитанных значений продольной силы строится ее эпюра (рис.1.8)
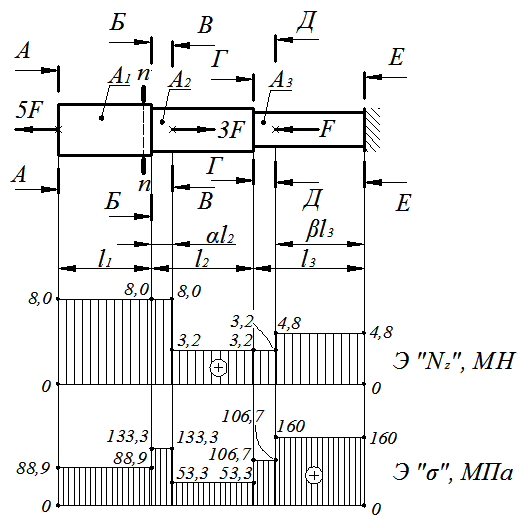
Рис. 1.8
Задача 1.2
Расчетная схема стержня показана на рис.1.9.
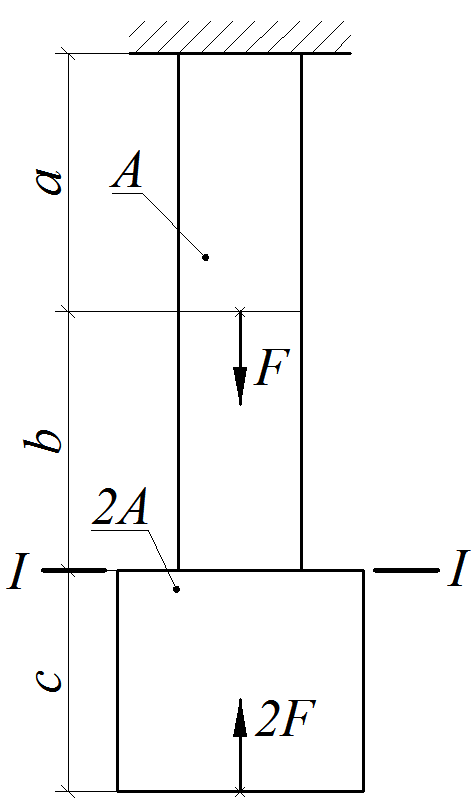
Рис. 1.9
Заданные величины:
1. Внешние силовые факторы:
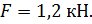
2. Площадь поперечного сечения ступеней стержня:
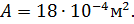
3. Длины силовых участков:
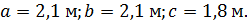
4. Модуль упругости и плотность материала:
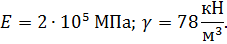
Требуется:
1. Построить эпюру продольных сил.
2. Построить эпюру нормальных напряжений.
3. Определить перемещение центра тяжести сечения I– I.
Решение
Рис.1.10
Условие равновесия отсеченной части
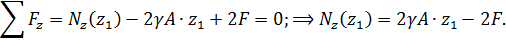
Продольная сила линейно зависит от координаты 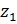 . Для построения эпюры ее значение необходимо определить в начале и конце силового участка:
. Для построения эпюры ее значение необходимо определить в начале и конце силового участка:
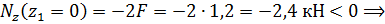
продольная сила является сжимающей.
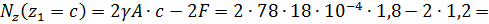
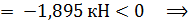 продольная сила является сжимающей.
продольная сила является сжимающей.
2-й силовой участок, ( 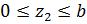 ), рис. 1.11.
), рис. 1.11.
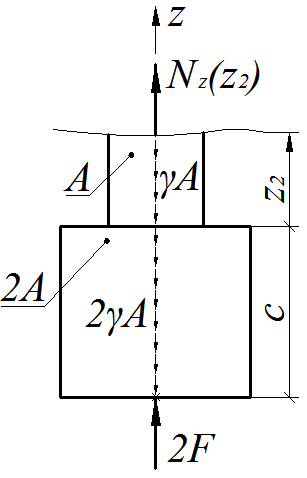
Рис.1.11
Условие равновесия отсеченной части
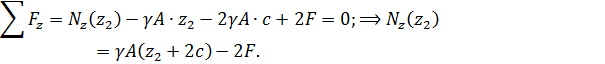
Продольная сила линейно зависит от координаты 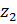 . Для построения эпюры ее значение необходимо определить в начале и конце силового участка:
. Для построения эпюры ее значение необходимо определить в начале и конце силового участка:
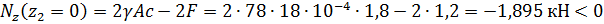
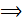 продольная сила является сжимающей.
продольная сила является сжимающей.
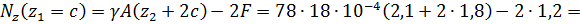
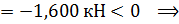 продольная сила является сжимающей.
продольная сила является сжимающей.
3-й силовой участок, ( 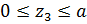 ), рис. 1.12.
), рис. 1.12.
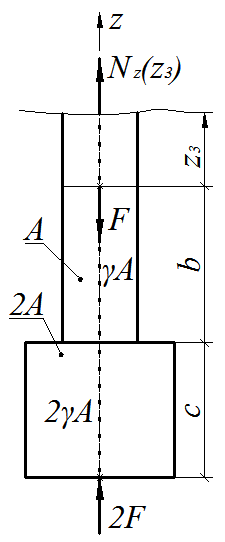
Рис.1.12
Условие равновесия отсеченной части
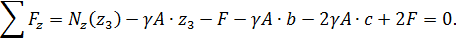
Выражение для продольной силы имеет вид
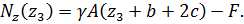
Продольная сила линейно зависит от координаты 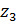 . Для построения эпюры ее значение необходимо определить в начале и конце силового участка:
. Для построения эпюры ее значение необходимо определить в начале и конце силового участка:

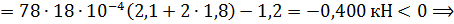
продольная сила является сжимающей.
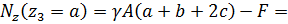
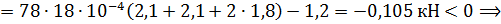
продольная сила является сжимающей.
На основании рассчитанных значений продольной силы строится ее эпюра (рис.1.13).Таким образом, внутренние силовые факторы определены.

Рис. 1.13
Определения перемещения заданного сечения I–I
Определение деформационных перемещений начинается от заделки (сечение А–А, см. рис. 1.13), поскольку заведомо известно
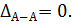
Перемещение остальных характерных сечений (м) определяется по формуле
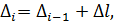
где 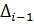 – перемещение предыдущего характерного сечения, м;
– перемещение предыдущего характерного сечения, м; 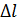 – абсолютное удлинение силового участка, заключенного между рассматриваемыми сечениями, м.
– абсолютное удлинение силового участка, заключенного между рассматриваемыми сечениями, м.
При постоянной жесткости в пределах участка
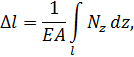
где 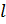 – длина силового участка, м.
– длина силового участка, м.
Сечение Б–Б:
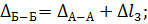
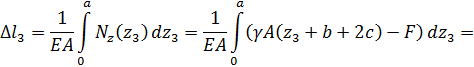
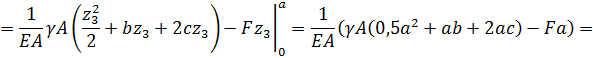
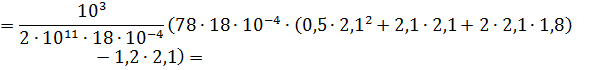
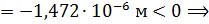
участок3 укорачивается.
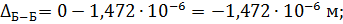
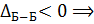
перемещение направлено к заделке, вверх.
Сечение В–В:
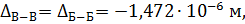
поскольку сечения В–В и Б–Б совпадают.
Сечение I–I:
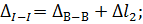
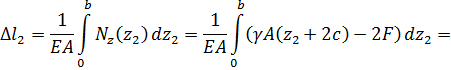
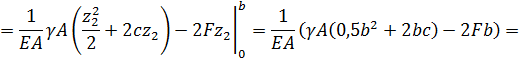
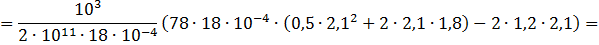
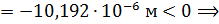
участок 2 укорачивается.
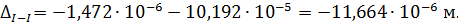
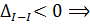
перемещение направлено к заделке, вверх.
Таким образом, искомое перемещение определено.
Задача 1.3
Расчетная схема стержня показана на рис. 1.14.
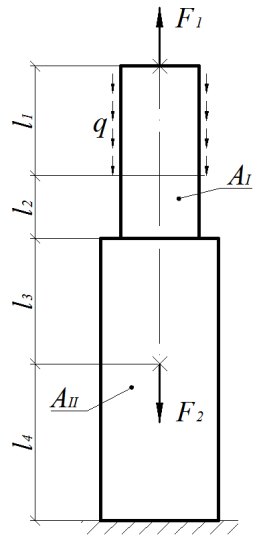
Рис. 1.14
Заданные величины:
1. Внешние силовые факторы:
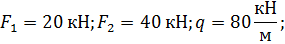
2. Материал – чугун, предел прочности на растяжение 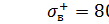 , предел прочности на сжатие
, предел прочности на сжатие 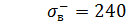 модуль упругости материала
модуль упругости материала 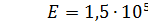
3. Коэффициент запаса прочности:
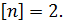
4. Длины силовых участков:
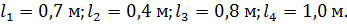
Требуется:
1. Построить эпюру продольных сил.
2. Из расчета на прочность определить безопасные размеры круглого поперечного сечения ступеней стержня.
3. Построить эпюру нормальных напряжений.
4. Определить перемещение свободного конца стержня.
Решение
Рис. 1.15
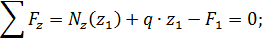
Линейная зависимость

Значения определяются в двух точках:
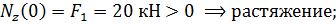
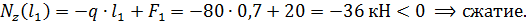
2-й участок, ( 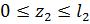 ),рис.1.16.
),рис.1.16.
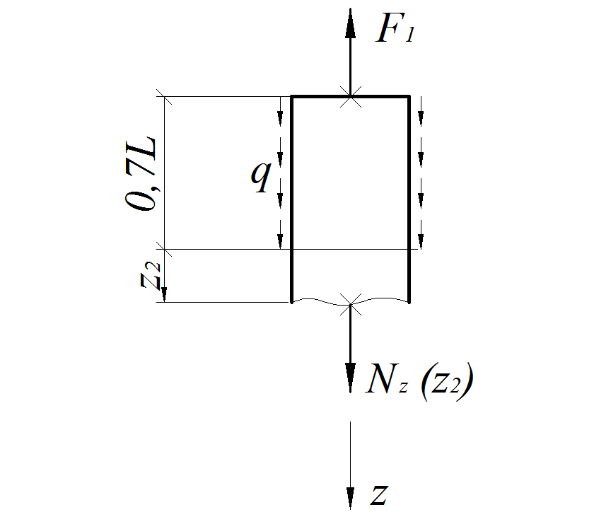
Рис. 1.16
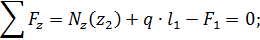
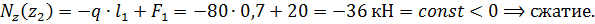
3-й участок, ( 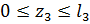 ),рис.1.17.
),рис.1.17.
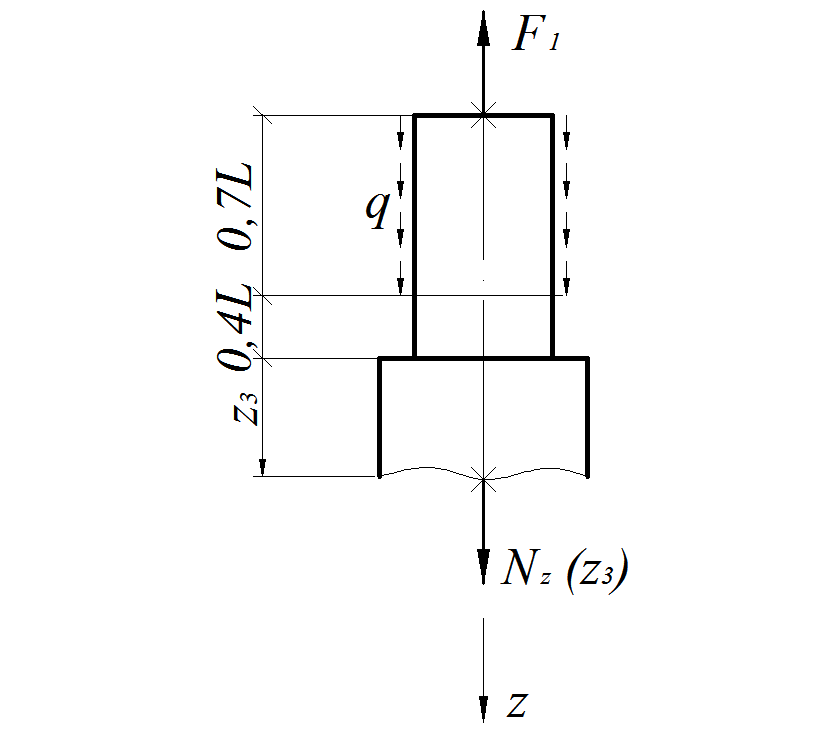
Рис. 1.17
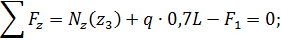
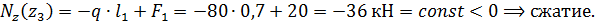
4-й участок, ( 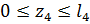 ),рис.1.18.
),рис.1.18.
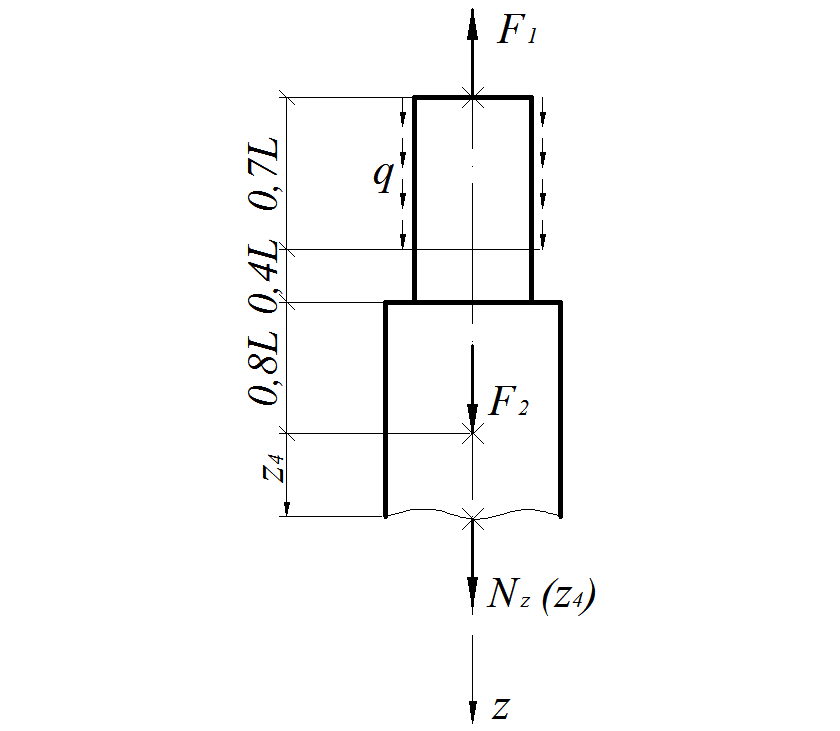
Рис. 1.18
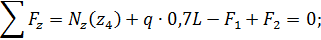
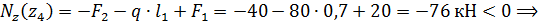
На основании полученных значений строится эпюра продольной силы (рис.1.19).
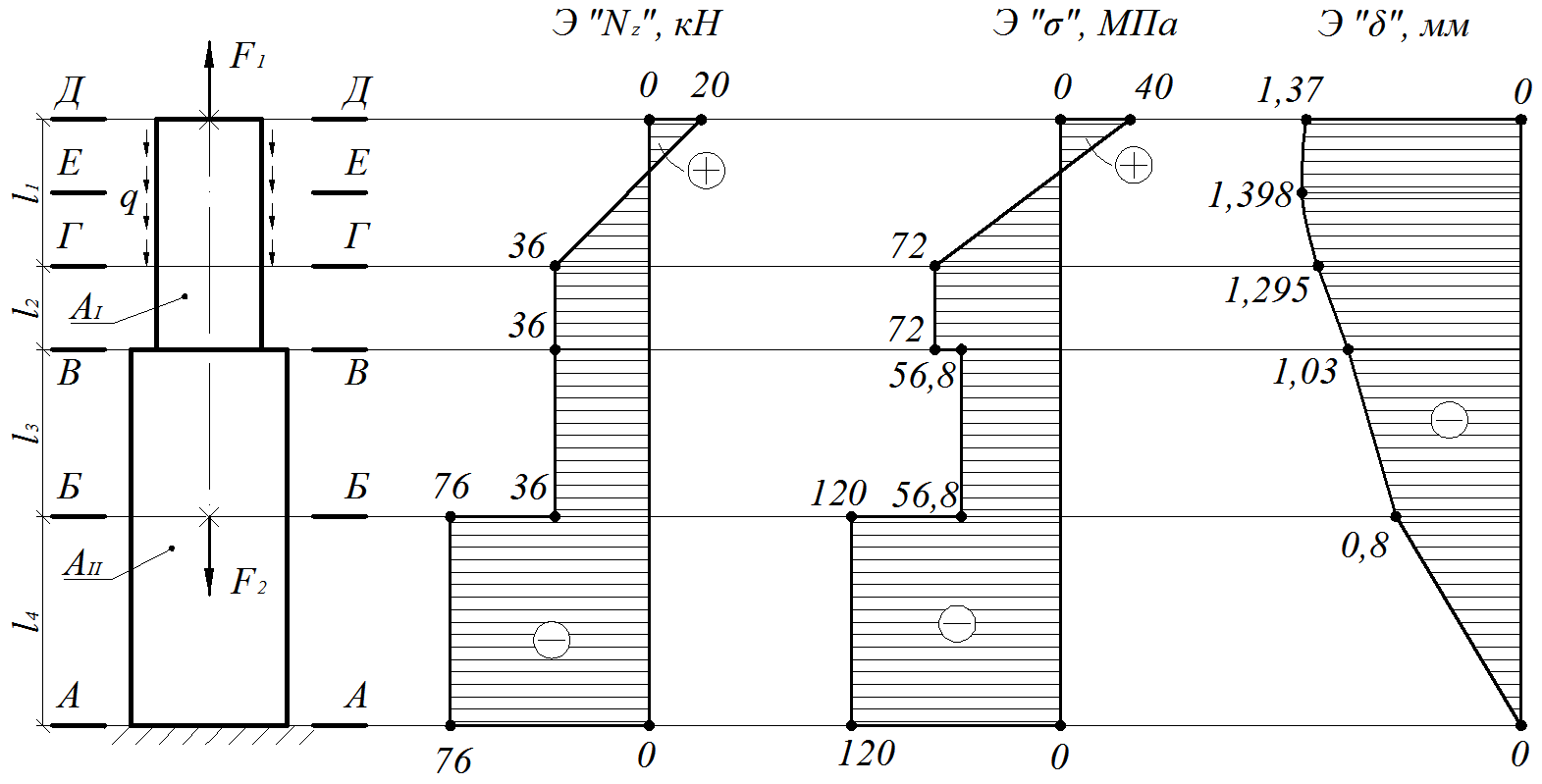
Рис. 1.19
Задания к разделу 1
Для заданной схемы стержня (табл. 1.1) требуется:
1. Составить аналитические выражения и построить эпюру продольных сил.
2. Из расчета на прочность определить требуемые диаметры ступеней стержня.
3. Построить эпюру напряжений в поперечных сечениях стержня.
4. Построить эпюру перемещений сечений стержня.
Таблица 1.1
Раздел 1. РАСЧЕТ СТЕРЖНЕЙ ПРИ РАСТЯЖЕНИИ-СЖАТИИ
Задача 1.1
Расчетная схема стержня показана на рис.1.1.

Рис.1.1
Заданные величины:
1. Внешние силовые факторы:
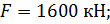
2. Площадь поперечного сечения ступеней стержня:
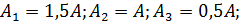
3. Длины силовых участков:
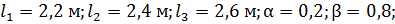
4. Характеристики прочности и упругости материала:
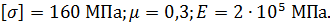
Требуется:
1. Построить эпюру продольных сил.
2. Определить площади поперечных сечений каждой ступени стержня.
3. Построить эпюру нормальных напряжений.
4. Вычислить полную абсолютную деформацию стержня.
5. Найти относительную продольную и относительную поперечную деформацию участка с заданным сечением n – n.
Решение
Дата: 2019-02-02, просмотров: 850.