Если твердое тело вращается вокруг закрепленной оси z и известна зависимость угла поворота 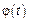, то можно рассчитать проекции на ось вращения его угловой скорости  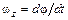и углового ускорения .

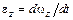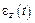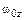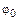Если известна зависимость  и начальные условия  и , то можно найт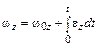и  и 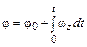 (обратная задача).

5-1. Диск радиуса  м начал вращаться вокруг своей оси без начальной скорости с угловым ускорением, зависящим от времени по закону 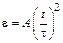. На какой угол (в радианах) он повернется за время  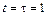с, если А = 1 с^–2.

5-2. Диск радиуса  м вращался вокруг своей оси с угловой скоростью 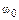. В момент времени  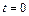его угловое ускорение стало возрастать по закону 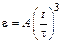. Какую угловую скорость будет иметь диск через время  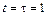с, если А = 1 с^–2,  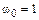с^–1.

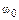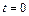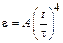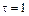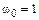5-3. Диск радиуса  м вращался вокруг своей оси с угловой скоростью . В момент времени  он начал тормозить. Модуль его углового ускорения при этом зависел от времени по закону , А = 5 с^–2. Через сколько секунд диск остановится, если  с,  с^–1?

5-4. Диск радиуса  м начал вращаться вокруг своей оси так, что угол его поворота зависит от времени по закону 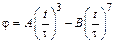. Через сколько секунд диск остановится, если  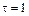с? А = 1 рад, В = 1 рад.

5-5. Диск радиуса 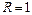 м вращался вокруг своей оси с угловой скоростью 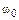. В момент времени  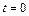его угловое ускорение стало возрастать по закону 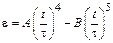. Через сколько секунд диск будет иметь максимальную угловую скорость, если  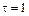с,  А = B = c^–2,  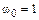с^–1.

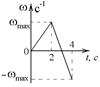5-6. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком (см. рис.). Найти угол поворота (в радианах) диска за  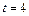с, если  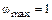с^–1.

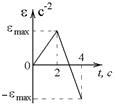
5-7. Диск вращается с нулевой начальной скоростью и с угловым ускорением, зависимость от времени которого задается графиком. Найти максимальную угловую скорость диска в интервале времени 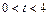 с, если  с^–2.

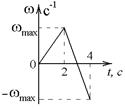5-8. Диск вращается с угловой скоростью, зависимость от времени которой задается графиком.

Найти максимальный угол поворота диска (в радианах) в интервале времени от t = 0 до 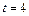 с, если  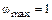с^–1.

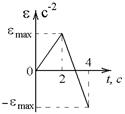
5-9. Диск вращается с угловым ускорением, зависимость от времени которого задается графиком. Найти угловую скорость диска в момент времени 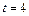 с, если  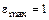с^–2.

5-10. Частица движется вдоль окружности с радиусом 1 м в соответствии с уравнением 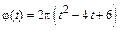, где 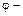угол в радианах, 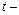время в секундах. Определить момент времени, когда величина нормального ускорения частицы равна нулю.

3.6. Сила как причина изменения импульса

Второй закон Ньютона в современной формулировк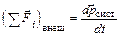е , где 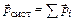 – суммарный импульс системы частиц,  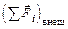– векторная сумма всех внешних сил, действующих на систему частиц.

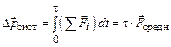 – вектор изменения импульса за время t (импульс силы), где  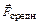– средняя сила, действующая на систему частиц.

В проекциях , , .  ; ; ;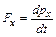

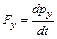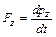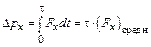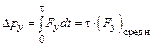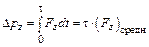Модуль изменения импульса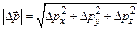

Модуль силы 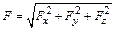, модуль импульса .

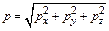6-1. Частица движется в плоскости так, что ее импульс зависит от времени по закону

. Найти модуль силы, действующей на частицу в момент времени 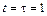 с, если А = В = 1 .

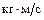6-2. Частица движется в плоскости так, что ее импульс зависит от времени по закону 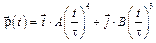. Найти тангенс угла между осью х и вектором силы, действующей на частицу в момент времени  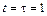с, если А =В = 1 .

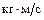6-3. Частица движется в плоскости так, что ее импульс зависит от времени по закону а) 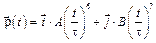. Найти тангенс угла между осью y и вектором силы, действующей на частицу в момент времени  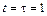с, если А = В = 1 .

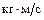6-4. Частица массы m = 1 кг движется в плоскости так, что ее импульс зависит от времени по закону

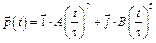. Найти ускорение частицы в момент времени  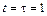с, если А = В = 1 .

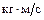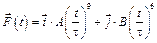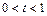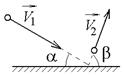
6-5. Частица движется в плоскости под действием силы, которая зависит от времени по закону .Найти модуль изменения импульса за интервал времени  с, если 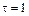 с, А = В = 1 Н.

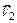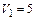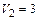6-6. Небольшой шарик массы m летит со скоростью  под углом a =30° к горизонтальной плоскости. После неупругого удара он отскакивает со скоростью  под углом b =60° к плоскости. Время соударения t. Найти модуль средней силы трения шарика о плоскость, действовавшей во время удара, если  м/с,  м/с, t = 0,001 с, m = 1 кг.

6-7. Частица с начальным импульсом 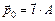 движется в плоскости под действием силы, которая зависит от времени по закону

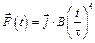. Найти модуль импульса через t = t = 1 с, если А = 1 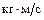, В = 1 Н.

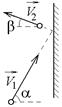6-8. Небольшой шарик массы m летит со скоростью  под углом a = 60° к горизонту и падает на вертикальную стену. После неупругого удара он отскакивает со скоростью 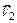 под углом b =30° к горизонту. Время соударения t. Найти модуль средней силы нормальной реакции со стороны стены.

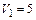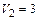Если  м/с,  м/с, t = 0,001 с, m = 1 кг.

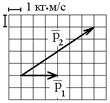6-9. Теннисный мяч летел с импульсом  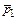в горизонтальном направлении, когда теннисист произвел по мячу резкий удар длительностью 0,1 с. Изменившийся импульс мяча стал равным 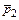 (масштаб указан на рисунке). Найти среднюю силу удара.

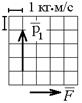6-10. Теннисный мяч летел с импульсом  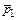(масштаб и направление указаны на рисунке). В перпендикулярном направлении на короткое время  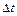= 0,1 с на мяч подействовал порыв ветра с постоянной силой F = 40 Н. Какова стала величина импульса p₂ после того, как ветер утих?