Стоимость решения одной контрольной работы из этой методички (кр1 - 12 задач или кр2 - конспект) всего
Рублей
Уважаемые студенты, по всем вопросам обращайтесь к администраторам группы https://vk.com/infoprint71, по электронной почте infoprint0@yandex.ru, по форме заказа на сайте infoprint5.ru, в офис по адресу: г.Новомосковск, ул. Дзержинского 13, офис №108, или по форме отправки сообщений (справа верху под аватаркой). Звоните по телефону 8-919-076-33-01.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Тульский государственный университет»
Кафедра физики
ВВЕДЕНИЕ В ФИЗИКУ
Методические указания и контрольные задания
для студентов заочной формы обучения
Тула 2012
УДК 531
Введение в физику. Методические указания и контрольные задания для студентов заочной формы обучения / Муравлева Л.В., Семин В.А., Бурцева О.И., Кажарская С.Е.- Тула: Изд-во ТулГУ, 2012. – 47 с.
Данные методические указания содержат краткие сведения из теории, набор контрольных заданий, краткое математическое приложение и общие методические указания к выполнению контрольных работ.
Ил.:62, Библ.: 9
Печатается по решению библиотечно-издательского совета Тульского государственного университета.
Рецензент: д-р физ.-мат.наук, проф. Д.М.Левин
ОГЛАВЛЕНИЕ
1. Общие методические указания к выполнению
контрольных работ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2. Основы векторной алгебры и математического анализа
2.1. Скалярные и векторные величины . . . . . . . . . . . . . . . . . . . 6
2.2. Действия с векторами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.1 Сравнение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.2 Сложение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.3 Вычитание векторов . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.2.4 Умножение вектора на скаляр . . . . . . . . . . . . . . . . . .10
2.3. Скалярное и векторное произведения . . . . . . . . . . . . . . . . 10
2.3.1 Скалярное произведение . . . . . . . . . . . . . . . . . . . . . . 10
2.3.2 Векторное произведение . . . . . . . . . . . . . . . . . . . . . . 10
2.4. Производная и интеграл . . .. . . . . . . . . . . . . . . . . . . . . . . . .12
2.4.1. Производная и ее применения . . . . . . . . . . . . . . . . . 12
2.4.2. Первообразная и интеграл . . . . . . . . . . . . . . . . . . . . .14
3.Задания для контрольной работы по дисциплине
«Введениие в физику»
3.1. Основы векторной алгебры . . . . . . . . . . . . . . . . . . . . . . . . . 16
3.2. Прямая задача кинематики. Векторный способ
описания движения частицы . . . . . . . . . . . . . . . . . . . . . . . . . . . .19
3.3. Обратная задача кинематики . . . . . . . . . . . . . . . . . . . . . . . .22
3.4. Связь линейных и угловых величин в кинематике . . . . . .26
3.5. Кинематика вращательного движения . . . . . . . . . . . . . . . . 28
3.6. Сила как причина изменения импульса . . . . . . . . . . . . . . . 30
3.7. Динамика вращательного движения твердого тела . . . . . .33
3.8. Момент инерции. Теорема Штейнера. Центр масс . . . . . .36
3.9. Кинетическая энергия. Мощность. Работа . . . . . . . . . . . . .41
3.10. Закон сохранения импульса и момента импульса . . . . . .43
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Общие методические указания к выполнению
Контрольных работ
- В течение первого семестра студент-заочник выполняет контрольную работу №1 и №2 по дисциплине «Введение в физику». Контрольная работа №1 предусматривает решение задач. Номера задач, которые студент должен включить в контрольную работу определяются по таблице вариантов, приведенной ниже. Последняя цифра зачетной книжки соответствует номеру варианта.
Контрольная работа №2 заключается в написании конспекта по физике в соответствии с перечнем тем, приведенных ниже. Объем конспекта должен составлять не менее 10 машинописных листов.
2. Контрольные работы нужно выполнять чернилами в школьной тетради в клетку или на листах формата А4. На обложке контрольных необходимо привести сведения по следующему образцу:
Контрольная работа №1 (№2)
По дисциплине «Введение в физику»
Вариант № 1
выполнил: студент группа Б660121 Иванов П.П.
В А Р И А Н Т Ы
Перечень тем к контрольной работе № 2 по дисциплине
«Введение в физику»
Кинематика.
Материальная точка. Система отсчета. Путь и перемещение. Поступательное и вращательное движение. Средняя скорость прохождения пути. Мгновенная скорость. Ускорение. Равномерное прямолинейное движение. Равнопеременное прямолинейное движение. Прямая и обратная задачи кинематики. Сложение скоростей. Кинематика вращательного движения. Тангенциальное и нормальное ускорение, радиус кривизны. Период и частота обращения. Связь линейных и угловых величин в кинематике.
Динамика.
Инертность тел. Инерциальная система отсчета. Первый закон Ньютона. Взаимодействие тел. Сила. Сложение сил. Второй закон Ньютона. Сила как причина изменения импульса. Третий закон Ньютона. Закон всемирного тяготения. Сила тяжести. Вес тела. Невесомость. Импульс тела. Импульс силы. Закон сохранения импульса. Реактивное движение. Момент инерции тела. Момент импульса материальной точки и момент силы. Закон сохранения момента импульса. Уравнение динамики вращательного движения.
Механическая работа. Кинетическая энергия. Потенциальная энергия. Работа силы тяжести, силы упругости и гравитационной силы. Закон сохранения механической энергии. Мощность. Коэффициент полезного действия.
Действия с векторами
Математические действия с векторными величинами – это геометрические действия.
Сравнение векторов
Равные векторы. Два вектора равны, если они имеют:
- равные модули,
- одинаковые направления.
Противоположные векторы. Два вектора противоположны, если они имеют:
- равные модули,
- противоположные направления.
-
Сложение векторов
Мы можем сложить два вектора геометрически по правилу параллелограмма и по правилу треугольника.
Пусть заданы два вектора 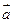 и
и 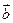 (см. рис.). Найдем сумму этих векторов
(см. рис.). Найдем сумму этих векторов 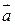 +
+ 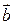 =
= 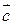 . Величины
. Величины 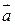 и
и 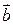 - это составляющие векторы, вектор
- это составляющие векторы, вектор 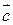 - это результирующий вектор.
- это результирующий вектор.
Правило параллелограмма для сложения двух векторов:
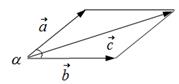 1. Нарисуем вектор
1. Нарисуем вектор 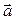 .
.
2. Нарисуем вектор 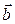 так, что его начало совпадает с началом вектора
так, что его начало совпадает с началом вектора 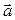 ; угол между векторами равен
; угол между векторами равен 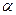 (см. рисунок).
(см. рисунок).
3. Через конец вектора 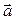 проведем прямую линию, параллельную вектору
проведем прямую линию, параллельную вектору 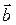 .
.
4. Через конец вектора 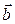 проведем прямую линию, параллельную вектору
проведем прямую линию, параллельную вектору 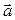 .
.
Мы построили параллелограмм. Стороны этого параллелограмма – составляющие векторы 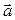 и
и 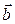 .
.
5. Проведем диагональ параллелограмма из общей точки начала вектора 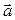 и начала вектора
и начала вектора 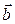 .
.
6. Модуль результирующего вектора 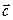 равен длине диагонали параллелограмма и определяется по формуле:
равен длине диагонали параллелограмма и определяется по формуле:
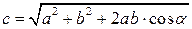 ;
;
начало вектора 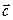 совпадает с началом вектора
совпадает с началом вектора 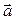 и началом вектора
и началом вектора 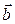 (направление вектора
(направление вектора 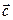 показано на рисунке).
показано на рисунке).
Правило треугольника для сложения двух векторов:
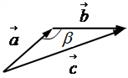
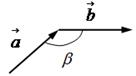
1. Нарисуем составляющие векторы 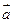 и
и 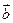 так, что начало вектора
так, что начало вектора 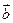 совпадает с концом вектора
совпадает с концом вектора 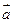 . При этом угол между векторами равен
. При этом угол между векторами равен 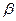 .
.
2. Результирующий вектор 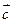 направлен так, что его начало совпадает с началом вектора
направлен так, что его начало совпадает с началом вектора 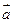 , а конец совпадает с концом вектора
, а конец совпадает с концом вектора 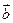 .
.
3. Модуль результирующего вектора находим по формуле:
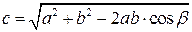
Вычитание векторов
Вычитание векторов – это действие, обратное сложению:
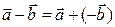
Найти разность вектора 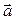 и вектора
и вектора 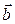 - это тоже самое, что найти сумму вектора
- это тоже самое, что найти сумму вектора 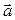 и вектора
и вектора 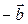 , противоположного вектору
, противоположного вектору 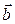 . Мы можем найти вектор разности геометрически по правилу параллелограмма или по правилу треугольника (см. рис.).
. Мы можем найти вектор разности геометрически по правилу параллелограмма или по правилу треугольника (см. рис.).
Правило параллелограмма.
Стороны параллелограмма - вектор 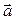 и вектор -
и вектор - 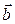 ; диагональ параллелограмма - вектор разности
; диагональ параллелограмма - вектор разности 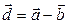 .
.
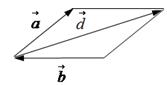
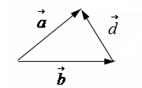
Правило треугольника.
Вектор разности 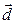 соединяет конец вектора
соединяет конец вектора 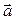 и конец вектора
и конец вектора 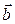 (начало вектора
(начало вектора 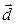 совпадает с концом вектора
совпадает с концом вектора  ).
).
Умножение вектора на скаляр
Пусть заданы вектор 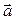 и скаляр n. Найдем произведение вектора
и скаляр n. Найдем произведение вектора 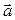 и скалярного вектора n.
и скалярного вектора n.
В результате умножения вектора на скаляр мы получаем новый вектор 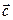 :
: 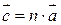
Направление вектора 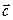 такое же, как направление вектора
такое же, как направление вектора 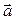 при
при 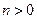 .
.
Направление вектора 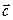 противоположно направлению вектора
противоположно направлению вектора 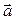 при
при 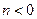 .
.
Модуль вектора 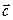 в n раз больше модуля вектора
в n раз больше модуля вектора 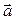 , если
, если 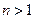 .
.
Скалярное произведение
Из двух векторов 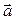 и
и 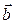 можно образовать скаляр по правилу:
можно образовать скаляр по правилу:
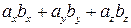
Это выражение называется скалярным произведением векторов 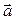 и
и 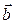 и обозначается одним из символов
и обозначается одним из символов 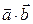 , или
, или 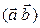 .
.
Следовательно, 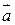 .
. 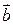 =
= 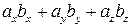 .
.
По определению скалярное произведение обладает следующими свойствами:
1) 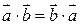 ,
,
2) 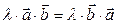 ,
,
3) 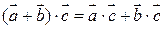
Векторное произведение
Из двух векторов 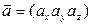 и
и 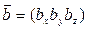 можно образовать новый вектор:
можно образовать новый вектор:
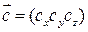 , где
, где
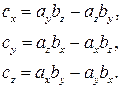
Модуль нового результирующего вектора находим по формуле:
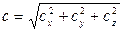 .
.
Эта операция называется векторным произведением векторов 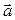 и
и 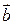 и обозначается одним из символов
и обозначается одним из символов 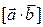 или
или 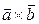 .
.
Также общеизвестна формула
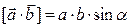 ,
,
где 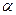 - угол между векторами
- угол между векторами 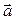 и
и 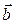 .
.
Направление вектора 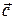 можно найти, используя следующий прием. Мысленно совмещаем продольную ось буравчика (правого винта, штопора) с перпендикуляром к плоскости, в которой лежат перемножаемые векторы (в данном примере – векторы
можно найти, используя следующий прием. Мысленно совмещаем продольную ось буравчика (правого винта, штопора) с перпендикуляром к плоскости, в которой лежат перемножаемые векторы (в данном примере – векторы 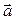 и
и 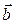 ). Затем начинаем вращать головку винта (ручку штопора) по направлению кратчайшего поворота от первого сомножителя ко второму, то есть от вектора
). Затем начинаем вращать головку винта (ручку штопора) по направлению кратчайшего поворота от первого сомножителя ко второму, то есть от вектора 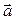 к вектору
к вектору 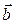 . Направление движения тела винта и будет являться направлением вектора
. Направление движения тела винта и будет являться направлением вектора 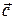 . Этот прием называется правилом правого винта или правилом буравчика (см. рис.).
. Этот прием называется правилом правого винта или правилом буравчика (см. рис.).
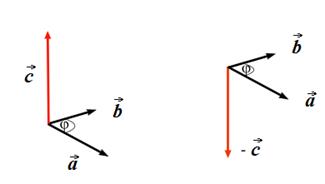
В терминах векторного произведения выражаются момент силы, момент импульса и др. Говоря о векторе, всегда имеем ввиду его компоненты. Вектор, в отличие от скаляра, определяется тремя числами. Поэтому такие операции как сложение, вычитание, скалярное и векторное произведения сводятся к привычным действиям с компонентами.
Производная и интеграл
Производная и ее применения
Пусть функция у= f (х) определена в точках х и х1 .Разность х1 - х называется приращением аргумента, а разность f (х1) - f (х) - приращением функции при переходе от значения аргумента х к значению аргумента х1. Приращение аргумента обозначают 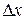 , приращение функции обозначают
, приращение функции обозначают 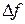 или
или 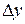 .
.
Если существует предел отношения приращения функции 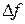 к приращению аргумента
к приращению аргумента 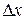 при условии, что
при условии, что 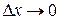 , то функция у= f (х) называется дифференцируемой в точке х, а этот предел называется значением производной функции у= f (х) в точке х и обозначается
, то функция у= f (х) называется дифференцируемой в точке х, а этот предел называется значением производной функции у= f (х) в точке х и обозначается 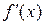 или
или 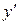 .
.
Операцию отыскания производной называют дифференцированием.
Первообразная и интеграл
Пусть на интервале (а, b) задана непрерывная функция f (х). По определению функция F (х) называется первообразной функцией для f (х) на интервале (а, b), если на нем производная от F (х) равна f (х):
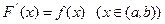
Очевидно, что если функция 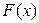 - первообразная для f (х) на (а, b), а С – некоторая постоянная, то функция
- первообразная для f (х) на (а, b), а С – некоторая постоянная, то функция 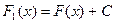 есть также первообразная для f (х), потому, что
есть также первообразная для f (х), потому, что
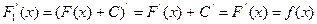
Если F (х) какая-либо первообразная от f (х) на интервале (а, b), то возможные первообразные от f (х) на этом интервале выражаются формулой 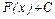 , где вместо С можно подставить любое число.
, где вместо С можно подставить любое число.
Неопределенным интегралом от непрерывной функции f (х) на интервале (а, b) называется произвольная ее первообразная функция. Неопределенный интеграл обозначается так:
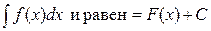 .
.
Если 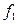 ,
, 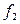 – непрерывные на интервале (а, b) функции и
– непрерывные на интервале (а, b) функции и 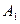 , и
, и 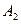 – постоянные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла:
– постоянные, то имеет место следующее равенство, выражающее основное свойство неопределенного интеграла:
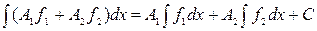 ,
,
где С – некоторая постоянная.
Список основных неопределенных интегралов
1. 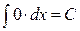 ;
;
2. 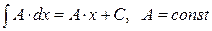 ;
;
3. 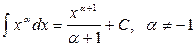 ;
;
4. 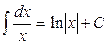 ;
;
5. 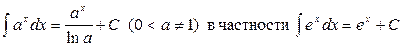 ;
;
6. 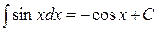 ;
;
7. 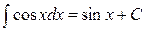 ;
;
8. 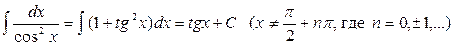
9. 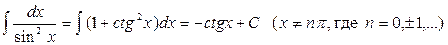
10. 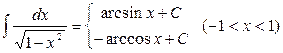 ;
;
11. 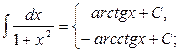
12. 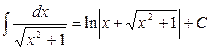 ;
;
13. 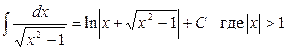 ;
;
14. 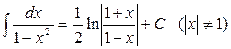
3.Задания для контрольной работы по дисциплине
«Введениие в физику»
Основы векторной алгебры
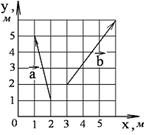
1-1. Найдите
а) модуль суммы 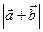
б) разности 
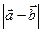 двух векторов
двух векторов  и
и  .
.
в) скалярное произведение векторов 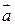 .
. 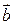
г) косинус угла между векторами  и
и 
д) векторное произведение 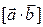 двух векторов
двух векторов  и
и 
Решить задачу графически и аналитически.
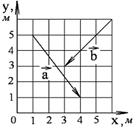
1-2. Найдите
а) модуль суммы 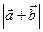
б) разности 
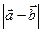 двух векторов
двух векторов  и
и  .
.
в) скалярное произведение векторов 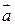 .
. 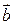
г) косинус угла между векторами  и
и 
д) векторное произведение 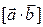 двух векторов
двух векторов  и
и 
Решить задачу графически и аналитически.
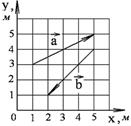
1-3. Найдите
а) модуль суммы 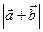
б) разности 
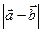 двух векторов
двух векторов  и
и  .
.
в) скалярное произведение векторов 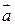 .
. 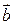
г) косинус угла между векторами  и
и 
д) векторное произведение 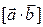 двух векторов
двух векторов  и
и 
Решить задачу графически и аналитически.
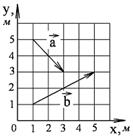 1-4. Найдите
1-4. Найдите
а) модуль суммы 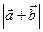
б) разности 
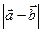 двух векторов
двух векторов  и
и  .
.
в) скалярное произведение векторов 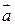 .
. 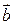
г) косинус угла между векторами  и
и 
д) векторное произведение 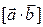 двух векторов
двух векторов  и
и 
Решить задачу графически и аналитически.
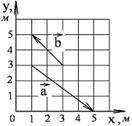
1-5. Найдите
а) модуль суммы 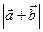
б) разности 
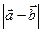 двух векторов
двух векторов  и
и  .
.
в) скалярное произведение векторов 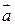 .
. 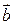
г) косинус угла между векторами  и
и 
д) векторное произведение 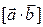 двух векторов
двух векторов  и
и 
Решить задачу графически и аналитически.
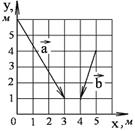
1-6. Найдите
а) модуль суммы 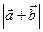
б) разности 
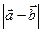 двух векторов
двух векторов  и
и  .
.
в) скалярное произведение векторов 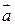 .
. 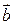
г) косинус угла между векторами  и
и 
д) векторное произведение 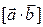 двух векторов
двух векторов  и
и 
Решить задачу графически и аналитически.
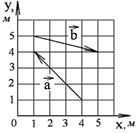 1-7. Найдите
1-7. Найдите
а) модуль суммы 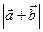
б) разности 
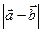 двух векторов
двух векторов  и
и  .
.
в) скалярное произведение векторов 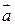 .
. 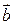
г) косинус угла между векторами  и
и 
д) векторное произведение 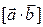 двух векторов
двух векторов  и
и 
Решить задачу графически и аналитически.
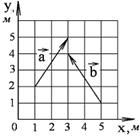
1-8. Найдите
а) модуль суммы 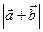
б) разности 
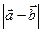 двух векторов
двух векторов 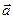 и
и  .
.
в) скалярное произведение векторов 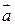 .
. 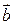
г) косинус угла между векторами 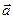 и
и 
д) векторное произведение 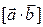 двух векторов
двух векторов 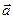 и
и 
Решить задачу графически и аналитически.
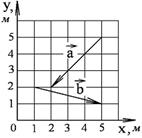
1-9. Найдите
а) модуль суммы 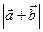
б) разности 
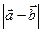 двух векторов
двух векторов 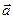 и
и  .
.
в) скалярное произведение векторов 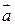 .
. 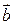
г) косинус угла между векторами 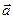 и
и 
д) векторное произведение 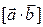 двух векторов
двух векторов 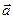 и
и 
Решить задачу графически и аналитически.
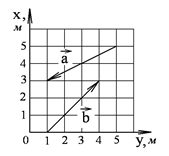 1-10. Найдите
1-10. Найдите
а) модуль суммы 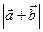
б) разности 
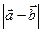 двух векторов
двух векторов 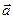 и
и  .
.
в) скалярное произведение векторов 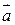 .
. 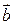
г) косинус угла между векторами 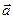 и
и 
д) векторное произведение 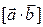 двух векторов
двух векторов 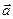 и
и 
Решить задачу графически и аналитически.
Прямая задача кинематики
Обратная задача кинематики
Если известны зависимости 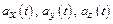 и начальные условия
и начальные условия 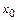 ,
, 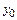 ,
, 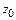 ,
, 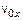 ,
, 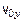 ,
, 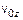 , то можно определить:
, то можно определить:
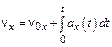 ;
; 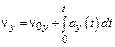 ;
; 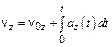
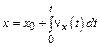 ;
; 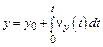 ;
; 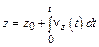
Путь, пройденный частицей за время t: 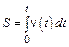
3-1. Частица начала свое движение из начала координат, и ее скорость зависит от времени по закону 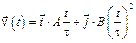 .
.
На какое расстояние от начала координат удалится частица в момент времени 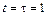 с, если А = В = 1 м/c.
с, если А = В = 1 м/c.
3-2. Частица начала свое движение из начала координат, и ее скорость зависит от времени по закону
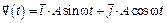 . Какой путь проделает частица за время
. Какой путь проделает частица за время 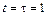 с, если А = В = 1 м/c,
с, если А = В = 1 м/c, 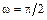 рад/с.
рад/с.
3-3. Частица начала свое движение из начала координат с нулевой начальной скоростью, и ее ускорение зависит от времени по закону 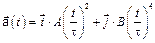 . Найти модуль скорости частицы в момент времени
. Найти модуль скорости частицы в момент времени 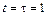 с, если А = В =1 м/с2.
с, если А = В =1 м/с2.
3-4. Частица начала свое движение из начала координат с нулевой начальной скоростью, и ее ускорение зависит от времени по закону 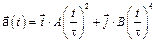 . Найти тангенс угла, под которым будет направлена скорость частицы в момент времени
. Найти тангенс угла, под которым будет направлена скорость частицы в момент времени 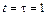 с а) к оси х, б) к оси y , если А = В =1 м/с2.
с а) к оси х, б) к оси y , если А = В =1 м/с2.
3-5. Частица начала свое движение из начала координат с начальной скоростью 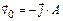 и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 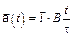 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 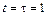 с, если А = 1 м/с, В =1 м/с2.
с, если А = 1 м/с, В =1 м/с2.
3-6. Частица начала свое движение из начала координат с начальной скоростью 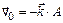 и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 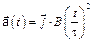 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 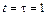 с, если А = 1 м/с, В =1 м/с2.
с, если А = 1 м/с, В =1 м/с2.
3-7. Частица начала свое движение из начала координат с начальной скоростью 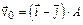 и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 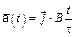 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 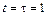 с, если А = 1 м/с, В =1 м/с2.
с, если А = 1 м/с, В =1 м/с2.
3-8. Частица начала свое движение из точки с радиусом-вектором 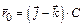 со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону 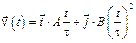 . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 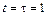 с, если А = В = 1 м/c, С = 1 м.
с, если А = В = 1 м/c, С = 1 м.
3-9. Частица начала свое движение из начала координат, и ее скорость зависит от времени по закону 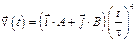 . Какой путь проделает частица за время
. Какой путь проделает частица за время 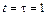 с, если А = В = 1 м/c.
с, если А = В = 1 м/c.
3-10. Частица начала свое движение из начала координат с нулевой начальной скоростью, и ее ускорение зависит от времени по закону 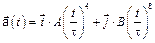 . Какая величина скорости будет у частицы в момент времени
. Какая величина скорости будет у частицы в момент времени 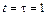 с, если А = 1 м/с2, В =1 м/с2.
с, если А = 1 м/с2, В =1 м/с2.
3-11. Частица начала свое движение из начала координат с начальной скоростью 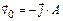 и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 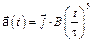 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 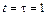 с, если А = 1 м/с, В =1 м/с2.
с, если А = 1 м/с, В =1 м/с2.
3-12. Частица начала свое движение из начала координат с начальной скоростью 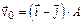 и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 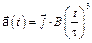 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 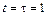 с, если А = 1 м/с, В =1 м/с2.
с, если А = 1 м/с, В =1 м/с2.
3-13. Частица начала свое движение из начала координат с начальной скоростью 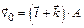 и с ускорением, которое зависит от времени по закону
и с ускорением, которое зависит от времени по закону 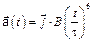 . Каков модуль скорости частицы в момент времени
. Каков модуль скорости частицы в момент времени 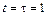 с, если А = 1 м/с, В =1 м/с2.
с, если А = 1 м/с, В =1 м/с2.
3-14. Частица начала свое движение из точки с радиусом-вектором 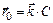 со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону 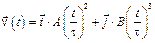 . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 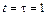 с, если А = В = 1 м/c, С = 1 м.
с, если А = В = 1 м/c, С = 1 м.
3-15. Частица начала свое движение из точки с радиусом-вектором 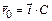 со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону 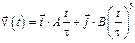 . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 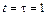 с, если А = В = 1 м/c, С = 1 м.
с, если А = В = 1 м/c, С = 1 м.
3-16. Частица начала свое движение из точки с радиусом-вектором 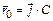 со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону 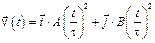 . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 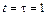 с, если А = В = 1 м/c, С = 1 м.
с, если А = В = 1 м/c, С = 1 м.
3-17. Частица начала свое движение из точки с радиусом-вектором 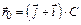 со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону 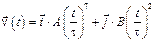 . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 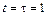 с, если А = В = 1 м/c, С = 1 м.
с, если А = В = 1 м/c, С = 1 м.
3-18. Частица начала свое движение из точки с радиусом-вектором 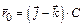 со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону
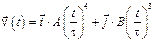 . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 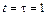 с, если А = В =1 м/c, С = 1 м.
с, если А = В =1 м/c, С = 1 м.
3-19. Начальная скорость частицы равна 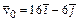 , а ускорение меняется во времени по закону
, а ускорение меняется во времени по закону 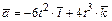 . Через сколько секунд скорость частицы окажется перпендикулярной оси ОХ?
. Через сколько секунд скорость частицы окажется перпендикулярной оси ОХ?
3-20. Частица начала свое движение из точки с радиусом-вектором 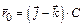 со скоростью, которая зависит от времени по закону
со скоростью, которая зависит от времени по закону
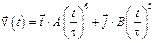 . На какое расстояние от начала координат удалится частица в момент времени
. На какое расстояние от начала координат удалится частица в момент времени 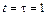 с, если А = В =1 м/c, С = 1 м.
с, если А = В =1 м/c, С = 1 м.
3.4. Связь линейных и угловых величин в кинематике
При криволинейном движении ускорение частицы имеет тангенциальную 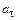 и нормальную
и нормальную 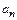 составляющие, причем
составляющие, причем 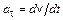 ,
, 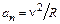 , где R – радиус кривизны траектории. Полное ускорение
, где R – радиус кривизны траектории. Полное ускорение 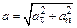 .
.
Линейные и угловые величины связаны следующим образом:
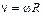 ;
; 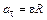 ;
; 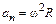
4-1. Частица из состояния покоя начала двигаться по дуге окружности радиуса 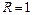 м с постоянным угловым ускорением
м с постоянным угловым ускорением 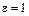 с–2. Найти
с–2. Найти
а) отношение тангенциального и нормального ускорения и
б) тангенс угла между вектором полного ускорения и вектором скорости частицы через время 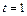 с?
с?
4-2. Частица из состояния покоя начала двигаться по дуге окружности радиуса 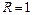 м со скоростью, модуль которой зависит от времени по закону
м со скоростью, модуль которой зависит от времени по закону 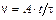 . Найти а) тангенс угла между вектором полного ускорения и вектором скорости частицы и б) отношение нормального и тангенциального ускорения частицы через время
. Найти а) тангенс угла между вектором полного ускорения и вектором скорости частицы и б) отношение нормального и тангенциального ускорения частицы через время 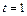 с, если
с, если 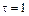 с, А = 1 м/с.
с, А = 1 м/с.
4-3. Частица из состояния покоя начала двигаться по дуге окружности радиуса 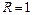 м с угловой скоростью, модуль которой зависит от времени по закону
м с угловой скоростью, модуль которой зависит от времени по закону 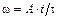 . Найти отношение нормального и тангенциального ускорения частицы через время
. Найти отношение нормального и тангенциального ускорения частицы через время 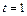 с, если
с, если 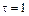 с. А = 1 с–1.
с. А = 1 с–1.
4-4. Частица из состояния покоя начала двигаться по дуге окружности радиуса 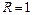 м с угловой скоростью, модуль которой зависит от времени по закону
м с угловой скоростью, модуль которой зависит от времени по закону 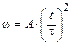 , А = 2 с–1. Через сколько секунд угол между полным ускорением частицы и ее скоростью будет равен 45°, если
, А = 2 с–1. Через сколько секунд угол между полным ускорением частицы и ее скоростью будет равен 45°, если 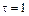 с.
с.
4-5. Частица из состояния покоя начала двигаться по дуге окружности радиуса 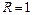 м так, что угол поворота зависит от времени по закону
м так, что угол поворота зависит от времени по закону 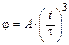 . Найти линейную скорость частицы через время
. Найти линейную скорость частицы через время 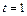 с, если
с, если 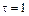 с. А = 1 рад.
с. А = 1 рад.
4-6. Частица из состояния покоя начала двигаться по дуге окружности радиуса 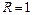 м так, что угол поворота зависит от времени по закону
м так, что угол поворота зависит от времени по закону 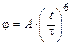 . Найти нормальное ускорение частицы через время
. Найти нормальное ускорение частицы через время 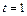 с, если
с, если 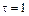 с. А = 1 рад.
с. А = 1 рад.
4-7. Частица из состояния покоя начала двигаться по дуге окружности радиуса 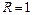 м так, что угол поворота зависит от времени по закону
м так, что угол поворота зависит от времени по закону 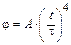 . Найти тангенциальное ускорение частицы через время
. Найти тангенциальное ускорение частицы через время 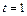 с, если
с, если 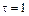 с. А = 1 рад.
с. А = 1 рад.
4-8. Частица из состояния покоя начала двигаться по дуге окружности радиуса 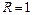 м с угловым ускорением, которое зависит от времени по закону
м с угловым ускорением, которое зависит от времени по закону 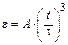 . Найти нормальное ускорение частицы через время
. Найти нормальное ускорение частицы через время 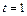 с, если
с, если 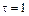 с. А = 1 с–2.
с. А = 1 с–2.
4-9. Частица из состояния покоя начала двигаться по дуге окружности радиуса 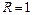 м с угловым ускорением, которое зависит от времени по закону
м с угловым ускорением, которое зависит от времени по закону 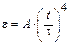 . Найти линейную скорость частицы через время
. Найти линейную скорость частицы через время 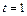 с, если
с, если 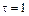 с. А = 1 с–2.
с. А = 1 с–2.
4-10. Скорость частицы изменяется во времени по закону 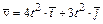 . Чему равна величина тангенциального ускорения частицы в момент времени t = 1 c?
. Чему равна величина тангенциального ускорения частицы в момент времени t = 1 c?
Теорема Штейнера.
Момент инерции 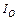 твердго тела относительно произвольной оси О равен сумме момента инерции этого тела
твердго тела относительно произвольной оси О равен сумме момента инерции этого тела 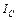 относительно оси С, параллельной оси О и проходящей через центр масс тела, и произведения массы этого тела
относительно оси С, параллельной оси О и проходящей через центр масс тела, и произведения массы этого тела 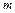 и квадрата расстояния
и квадрата расстояния 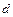 между осями О и С.
между осями О и С.
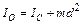
Координата центра масс 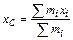 , где
, где 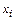 – координата материальной точки с массой
– координата материальной точки с массой 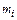 или
или 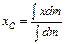 (случай непрерывного распределения).
(случай непрерывного распределения).
Таблица моментов инерции некоторых фигур.
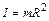 – кольца относительно оси, проходящей через центр кольца перпендикулярно его плоскости. – кольца относительно оси, проходящей через центр кольца перпендикулярно его плоскости.
| 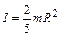 – однородного шара относительно оси, проходящей через центр шара. – однородного шара относительно оси, проходящей через центр шара.
|
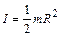 – диска относительно оси, проходящей через центр диска перпендикулярно его плоскости. – диска относительно оси, проходящей через центр диска перпендикулярно его плоскости.
| 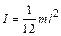 – стержня относительно оси, проходящей через середину стержня перпендикулярно к нему. – стержня относительно оси, проходящей через середину стержня перпендикулярно к нему.
|
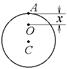 8-1. Перпендикулярно плоскости однородного диска массы m и радиуса R проходят две параллельные оси. Одна проходит через центр масс диска С, а другая через точку О, лежащую на расстоянии х от точки А на краю диска. Точки О, С и А лежат на диаметре диска. Во сколько раз больше момент инерции диска
8-1. Перпендикулярно плоскости однородного диска массы m и радиуса R проходят две параллельные оси. Одна проходит через центр масс диска С, а другая через точку О, лежащую на расстоянии х от точки А на краю диска. Точки О, С и А лежат на диаметре диска. Во сколько раз больше момент инерции диска 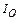 , чем
, чем 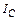 ? Если m = 1 кг, R = 1 м, х = 0,4 м.
? Если m = 1 кг, R = 1 м, х = 0,4 м.
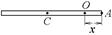 8-2. Перпендикулярно однородному тонкому стержню массы m и длиной l проходят две параллельные оси. Одна проходит через центр масс стержня С, а другая через точку О, лежащую на расстоянии х от его конца А. Во сколько раз больше момент инерции стержня
8-2. Перпендикулярно однородному тонкому стержню массы m и длиной l проходят две параллельные оси. Одна проходит через центр масс стержня С, а другая через точку О, лежащую на расстоянии х от его конца А. Во сколько раз больше момент инерции стержня 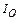 , чем
, чем 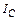 ? Если m = 1 кг, l = 1 м, х = 0,4 м.
? Если m = 1 кг, l = 1 м, х = 0,4 м.
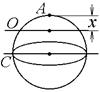 8-3. Через однородный шар массы m и радиуса R проходят две параллельные оси. Одна проходит через центр масс шара С, а другая через точку О, лежащую на расстоянии х от края шара A. Точки А, О и С лежат на диаметре шара. Во сколько раз больше момент инерции шара
8-3. Через однородный шар массы m и радиуса R проходят две параллельные оси. Одна проходит через центр масс шара С, а другая через точку О, лежащую на расстоянии х от края шара A. Точки А, О и С лежат на диаметре шара. Во сколько раз больше момент инерции шара 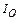 , чем
, чем 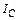 ? Если m = 1 кг, R = 1 м, х = 0,4 м.
? Если m = 1 кг, R = 1 м, х = 0,4 м.
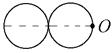 8-4. Два одинаковых диска массой m и радиусом R каждый положили на плоскость и приварили друг к другу. Найти момент инерции получившейся детали относительно оси, проходящей перпендикулярно плоскости дисков через точку О . Если R = 1 м, m = 1 кг.
8-4. Два одинаковых диска массой m и радиусом R каждый положили на плоскость и приварили друг к другу. Найти момент инерции получившейся детали относительно оси, проходящей перпендикулярно плоскости дисков через точку О . Если R = 1 м, m = 1 кг.
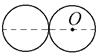 8-5. Два одинаковых диска массой m и радиусом R каждый положили на плоскость и приварили друг к другу. Найти момент инерции получившейся детали относительно оси, проходящей перпендикулярно плоскости дисков через центр масс одного из дисков О. R = 1 м, m = 1 кг.
8-5. Два одинаковых диска массой m и радиусом R каждый положили на плоскость и приварили друг к другу. Найти момент инерции получившейся детали относительно оси, проходящей перпендикулярно плоскости дисков через центр масс одного из дисков О. R = 1 м, m = 1 кг.
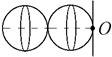 8-6. Два одинаковых шара массой m и радиусом R каждый приварили друг к другу. Касательная к шару ось О проходит перпендикулярно линии, проходящей через центры шаров. Найти момент инерции получившейся детали относительно оси О. R = 1 м, m = 1 кг.
8-6. Два одинаковых шара массой m и радиусом R каждый приварили друг к другу. Касательная к шару ось О проходит перпендикулярно линии, проходящей через центры шаров. Найти момент инерции получившейся детали относительно оси О. R = 1 м, m = 1 кг.
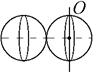 8-7. Два одинаковых шара массой m и радиусом R каждый приварили друг к другу. Ось О проходит по диаметру шара перпендикулярно линии, соединяющей центры шаров. Найти момент инерции получившейся детали относительно оси О.
8-7. Два одинаковых шара массой m и радиусом R каждый приварили друг к другу. Ось О проходит по диаметру шара перпендикулярно линии, соединяющей центры шаров. Найти момент инерции получившейся детали относительно оси О.
R = 1 м, m = 1 кг.
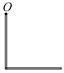 8-8. Два одинаковых однородных тонких стержня массой m и длиной l каждый приварили концами перпендикулярно друг к другу. Через конец одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О. l = 1 м, m = 1 кг.
8-8. Два одинаковых однородных тонких стержня массой m и длиной l каждый приварили концами перпендикулярно друг к другу. Через конец одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О. l = 1 м, m = 1 кг.
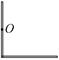 8-9. Два одинаковых однородных тонких стержня массой m и длиной l каждый приварили концами перпендикулярно друг к другу. Через центр одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О. l = 1 м, m = 1 кг.
8-9. Два одинаковых однородных тонких стержня массой m и длиной l каждый приварили концами перпендикулярно друг к другу. Через центр одного из стержней проходит ось О, перпендикулярная плоскости стержней. Найти момент инерции получившейся детали относительно оси О. l = 1 м, m = 1 кг.
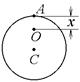 8-10. Перпендикулярно плоскости однородного диска массы m= 1 кг и радиуса R = 1 м проходят две параллельные оси. Одна проходит через центр масс диска С, а другая через точку О, лежащую на расстоянии х = 0,4 м от точки А на краю диска. Точки О, С и А лежат на диаметре диска. На сколько отличаются моменты инерции диска относительно этих осей?
8-10. Перпендикулярно плоскости однородного диска массы m= 1 кг и радиуса R = 1 м проходят две параллельные оси. Одна проходит через центр масс диска С, а другая через точку О, лежащую на расстоянии х = 0,4 м от точки А на краю диска. Точки О, С и А лежат на диаметре диска. На сколько отличаются моменты инерции диска относительно этих осей?
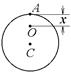 8-11. Перпендикулярно плоскости однородного диска массы m и радиуса R проходят две параллельные оси. Одна проходит через точку A на краю диска, а другая через точку О, лежащую на расстоянии х от точки А. Точки О и А лежат на диаметре диска. m = 1 кг, R = 1 м, х = 0,4 м. Во сколько раз отличаются моменты инерции диска
8-11. Перпендикулярно плоскости однородного диска массы m и радиуса R проходят две параллельные оси. Одна проходит через точку A на краю диска, а другая через точку О, лежащую на расстоянии х от точки А. Точки О и А лежат на диаметре диска. m = 1 кг, R = 1 м, х = 0,4 м. Во сколько раз отличаются моменты инерции диска 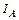 и
и 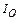 ?
?
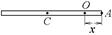 8-12. Перпендикулярно однородному тонкому стержню массы m = 1 кг и длиной l = 1 м проходят две параллельные оси. Одна проходит через центр масс стержня С, а другая через точку О, лежащую на расстоянии х = 0,4 м от его конца А. На сколько отличаются моменты инерции стержня относительно этих осей?
8-12. Перпендикулярно однородному тонкому стержню массы m = 1 кг и длиной l = 1 м проходят две параллельные оси. Одна проходит через центр масс стержня С, а другая через точку О, лежащую на расстоянии х = 0,4 м от его конца А. На сколько отличаются моменты инерции стержня относительно этих осей?
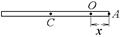 8-13. Перпендикулярно однородному тонкому стержню массы m = 1 кг и длиной l = 1 м проходят две параллельные оси. Одна проходит через конец стержня А, а другая через точку О, лежащую на расстоянии х = 0,4 м от точки А. Во сколько раз отличаются моменты инерции стержня
8-13. Перпендикулярно однородному тонкому стержню массы m = 1 кг и длиной l = 1 м проходят две параллельные оси. Одна проходит через конец стержня А, а другая через точку О, лежащую на расстоянии х = 0,4 м от точки А. Во сколько раз отличаются моменты инерции стержня 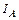 и
и 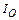 ?
?
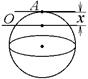 8-14. Через однородный шар массы m и радиуса R проходят две параллельные оси. Одна касается шара в точке А, а другая проходит через точку О, лежащую на расстоянии х от точки A. Точки А и О лежат на одном диаметре шара. m = 1 кг, R = 1 м, х = 0,4 м. Во сколько раз отличаются моменты инерции шара
8-14. Через однородный шар массы m и радиуса R проходят две параллельные оси. Одна касается шара в точке А, а другая проходит через точку О, лежащую на расстоянии х от точки A. Точки А и О лежат на одном диаметре шара. m = 1 кг, R = 1 м, х = 0,4 м. Во сколько раз отличаются моменты инерции шара 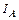 и
и 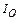 ?
?
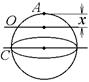 8-15. Через однородный шар массы m и радиуса R проходят две параллельные оси. Одна проходит через центр масс шара С, а другая через точку О, лежащую на расстоянии х от края шара A. Точки А, О и С лежат на диаметре шара. На сколько отличаются моменты инерции шара относительно этих осей? m = 1 кг, R = 1 м, х = 0,4 м.
8-15. Через однородный шар массы m и радиуса R проходят две параллельные оси. Одна проходит через центр масс шара С, а другая через точку О, лежащую на расстоянии х от края шара A. Точки А, О и С лежат на диаметре шара. На сколько отличаются моменты инерции шара относительно этих осей? m = 1 кг, R = 1 м, х = 0,4 м.
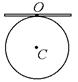 8-16. На одну плоскость положили тонкий однородный стержень массы m и длины l = 2R и диск радиуса R и такой же массы m. Центр стержня О приварили к диску. Перпендикулярно плоскости получившейся детали проходит ось через точку О. Найти момент инерции детали относительно этих осей. Если m = 1 кг, R = 1 м.
8-16. На одну плоскость положили тонкий однородный стержень массы m и длины l = 2R и диск радиуса R и такой же массы m. Центр стержня О приварили к диску. Перпендикулярно плоскости получившейся детали проходит ось через точку О. Найти момент инерции детали относительно этих осей. Если m = 1 кг, R = 1 м.
8-17. Деталь в виде равностороннего треугольника сварили из трех одинаковых однородных тонких стержней массы m и длины l каждый. Ось О проходит перпендикулярно плоскости детали через вершину треугольника. Найти момент инерции детали относительно этой оси. m = 1 кг, l = 1 м.
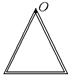
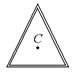 8-18. Деталь в виде равностороннего треугольника сварили из трех одинаковых однородных тонких стержней массы m и длины l каждый. Ось C проходит перпендикулярно плоскости детали через центр масс треугольника. Найти момент инерции детали относительно этой оси. m = 1 кг, l = 1 м.
8-18. Деталь в виде равностороннего треугольника сварили из трех одинаковых однородных тонких стержней массы m и длины l каждый. Ось C проходит перпендикулярно плоскости детали через центр масс треугольника. Найти момент инерции детали относительно этой оси. m = 1 кг, l = 1 м.
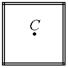 8-19. Деталь в виде квадрата сварили из четырех одинаковых однородных тонких стержней массы m и длины l каждый. Ось C проходит перпендикулярно плоскости детали через центр масс квадрата. Найти момент инерции детали относительно этой оси. m = 1 кг, l = 1 м.
8-19. Деталь в виде квадрата сварили из четырех одинаковых однородных тонких стержней массы m и длины l каждый. Ось C проходит перпендикулярно плоскости детали через центр масс квадрата. Найти момент инерции детали относительно этой оси. m = 1 кг, l = 1 м.
 8-20. Тонкий стержень постоянного сечения длиной l = 1 м лежит на оси х и его левый конец совпадает с началом координат О. Линейная плотность вещества, из которого сделан стержень, зависит от координаты х по закону (
8-20. Тонкий стержень постоянного сечения длиной l = 1 м лежит на оси х и его левый конец совпадает с началом координат О. Линейная плотность вещества, из которого сделан стержень, зависит от координаты х по закону ( 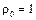 кг/м)
кг/м) 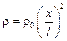 . Рассчитать момент инерции стержня относительно оси у.
. Рассчитать момент инерции стержня относительно оси у.
Литература
1. Савельев И.В. Курс общей физики : учебное пособие для вузов:[в 3 т.]. Т.1. Механика. Молекулярная физика / И.В. Савельев.- 5-е изд. стер. — СПб. и др.: Лань, 2006. - 432 с.
2. Савельев И.В. Сборник вопросов и задач по общей физике : учеб. пособие для втузов / И.В.Савельев .— СПб. и др. : Лань, 2005. - 288 с.
3. Стрелков С.П. Сборник задач по общему курсу физики : в 5 кн. - 5-е изд., стер .— М : Физматлит : Лань, 2006 .— (Общий курс физики). Кн. 1: Механика / С. П. Стрелков [и др.] ; под ред. И. А. Яковлева. - 2006. - 240 с.
4. Матвеев А.Н. Механика и теория относительности : Учебник для вузов / А.Н.Матвеев .- 3-е изд. - М. : ОНИКС 21 век: Мир и образование, 2003. - 432 с.
5. Трофимова Т.И. Сборник задач по курсу физики с решениями : учеб. пособие для вузов / Т.И.Трофимова .- 8-е изд. перераб. - М. : Высш. шк., 2007. - 591 с.
6. Трофимова Т.И. Основы физики : учеб. пособие:в 5 кн. Кн.1. Механика / Т.И.Трофимова .- М. : Высш. шк., 2007 .- 220с
7. Трофимова Т.И. Справочник по физике для студентов и абитуриентов / Т.И.Трофимова .— М. : Астрель:АСТ: Профиздат, 2005. - 399 с.
8. Яворский Б.М. Справочник по физике для инженеров и студентов вузов / Б. М. Яворский, А. А. Детлаф, А. К. Лебедев .- 8-е изд., перераб. и испр. - М. : ОНИКС : Мир и Образование, 2007. - 1055 с.
9. Полянин А.Д. Универсальный справочник. Высшая математика. Физика. Теоретическая механика. Сопротивление материалов / А.Д.Полянин [и др.].- М. : АСТ:Астрель: Профиздат, 2005. - 480 с.
Стоимость решения одной контрольной работы из этой методички (кр1 - 12 задач или кр2 - конспект) всего
Рублей
Уважаемые студенты, по всем вопросам обращайтесь к администраторам группы https://vk.com/infoprint71, по электронной почте infoprint0@yandex.ru, по форме заказа на сайте infoprint5.ru, в офис по адресу: г.Новомосковск, ул. Дзержинского 13, офис №108, или по форме отправки сообщений (справа верху под аватаркой). Звоните по телефону 8-919-076-33-01.
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
«Тульский государственный университет»
Кафедра физики
ВВЕДЕНИЕ В ФИЗИКУ
Методические указания и контрольные задания
для студентов заочной формы обучения
Тула 2012
УДК 531
Введение в физику. Методические указания и контрольные задания для студентов заочной формы обучения / Муравлева Л.В., Семин В.А., Бурцева О.И., Кажарская С.Е.- Тула: Изд-во ТулГУ, 2012. – 47 с.
Данные методические указания содержат краткие сведения из теории, набор контрольных заданий, краткое математическое приложение и общие методические указания к выполнению контрольных работ.
Ил.:62, Библ.: 9
Печатается по решению библиотечно-издательского совета Тульского государственного университета.
Рецензент: д-р физ.-мат.наук, проф. Д.М.Левин
ОГЛАВЛЕНИЕ
1. Общие методические указания к выполнению
контрольных работ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 4
2. Основы векторной алгебры и математического анализа
2.1. Скалярные и векторные величины . . . . . . . . . . . . . . . . . . . 6
2.2. Действия с векторами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.1 Сравнение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.2 Сложение векторов . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
2.2.3 Вычитание векторов . . . . . . . . . . . . . . . . . . . . . . . . . . 9
2.2.4 Умножение вектора на скаляр . . . . . . . . . . . . . . . . . .10
2.3. Скалярное и векторное произведения . . . . . . . . . . . . . . . . 10
2.3.1 Скалярное произведение . . . . . . . . . . . . . . . . . . . . . . 10
2.3.2 Векторное произведение . . . . . . . . . . . . . . . . . . . . . . 10
2.4. Производная и интеграл . . .. . . . . . . . . . . . . . . . . . . . . . . . .12
2.4.1. Производная и ее применения . . . . . . . . . . . . . . . . . 12
2.4.2. Первообразная и интеграл . . . . . . . . . . . . . . . . . . . . .14
3.Задания для контрольной работы по дисциплине
«Введениие в физику»
3.1. Основы векторной алгебры . . . . . . . . . . . . . . . . . . . . . . . . . 16
3.2. Прямая задача кинематики. Векторный способ
описания движения частицы . . . . . . . . . . . . . . . . . . . . . . . . . . . .19
3.3. Обратная задача кинематики . . . . . . . . . . . . . . . . . . . . . . . .22
3.4. Связь линейных и угловых величин в кинематике . . . . . .26
3.5. Кинематика вращательного движения . . . . . . . . . . . . . . . . 28
3.6. Сила как причина изменения импульса . . . . . . . . . . . . . . . 30
3.7. Динамика вращательного движения твердого тела . . . . . .33
3.8. Момент инерции. Теорема Штейнера. Центр масс . . . . . .36
3.9. Кинетическая энергия. Мощность. Работа . . . . . . . . . . . . .41
3.10. Закон сохранения импульса и момента импульса . . . . . .43
Литература . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47
Дата: 2018-12-28, просмотров: 605.