Если ученик натренировал сложение и умножение, но с вычитанием и делением у него остались трудности — делает ошибки, медленно считает — то можно потренировать их дополнительно. Таблицы вычитания и деления вы найдёте в конце книги. Тренировки по ним делаются по тем же принципам, что и для сложения и умножения.
УМНОЖЕНИЕ ЧИСЛА НА СКОБКУ И СКОБКИ НА СКОБКУ
Это действие, обычно разученное до автоматизма взрослыми и отличниками, может вызывать трудности у учеников. Справиться с этим можно так: подробно объяснить — что и зачем делается и попрактиковаться до ПОЛНОЙ уверенности. Эти действия должны стать «родными», как сложение и умножение.
УМНОЖЕНИЕ ЧИСЛА НА СКОБКУ
Если число умножают на скобку, в которой складываются два других числа, то получится тоже самое, если мы умножим число на первое число в скобке и сложим это с числом, умноженным на второе число в скобке.
А× (В + С) = А×В + А×С
Это легко проверить с небольшими числами:
3× (4 +1) = 3×4 +3×1 = 12 +3 = 15
Тоже самое получится, если мы сначала сделаем действия в скобках:
3× (4 +1) = 3×5 = 15
Это правило применяется при действиях с буквами, где мы не можем сложить А и В, а также для облегчения вычислений в некоторых случаях, например:
7 × 105 = 7 × (100 +5) = 7×100 +7×5 = 700 +35 = 735
Ещё одно применение этого правила — это вынесение за скобки общего множителя. Для примера выше это будет как бы выполнение действий в обратном порядке (от правой стороны выражения мы будем переходить к левой стороне выражения от знака =), например (общие множители подчёркнуты):
25 +35 = 5×5 +5×7 = 5 × (5 +7), или для букв:
А ×В + А×С = А × (В + С),
или 5 х +5у = 5 × (х + у),
или 5х +6х = (5+6) × х = 11х
УМНОЖЕНИЕ СКОБКИ НА СКОБКУ
Умножение скобки на скобку — это чуть более сложное применение того же правила:
(А + У) × (В + С) = АВ + АС + УВ + УС,
почему так — можно проверить, если мы заменим скобку (А + У) на Х, тогда будет
Х × (В + С) = ХВ + ХС
и если теперь мы поставим вместо Х снова (А + У), то получится:
ХВ + ХС = (А + У) ×В + (А + У) ×С = АВ + УВ + АС + УС
— то есть тоже самое, что в формуле, только в другом порядке, а от перестановки слагаемых сумма не меняется.
Запишем тоже самое с числами (по правилу умножения скобок):
(2 +3) × (4 +5) = 2×4 +2×5 +3×4 +3×5 = 8 +10 +12 +15 = 45
Или сначала вычислив в скобках:
(2 +3) × (4 +5) = 5 × 9 = 45
В математике часто можно вычислить значение или решить задачу несколькими разными способами. Но если всё делать без ошибок, то ответ будет тем же самым. Главное, чтобы вы были уверены в своём решении и всё делали по правилам.
ДРОБИ И ДЕЙСТВИЯ С НИМИ
Действия с дробями проходят через всю школьную математику. В жизни мы не очень много с ними сталкиваемся, хотя постоянно слышим и говорим — половина, четверть, треть. Но на всех экзаменах будут примеры на дроби и действия с ними. Очень редкие калькуляторы помогут вам в этом. Да ещё вам сначала придётся научиться использовать такой хитрый калькулятор. Довольно часто вычисления с дробями встречаются в физике, химии и изредка в биологии.
Дроби были придуманы людьми для того, чтобы справиться с проблемой деления с остатком.
8: 2 = 4 (ровно, без остатка), а 9: 2 = 4 и остаток 1.
Дробить — значит разбивать на более мелкие части. И в математике дробь — это что-то меньше, чем целая единица. Мне нравится использовать для примера тортики. Почему-то ученики с удовольствием придумывают способы для того, чтобы разделить тортики на несколько равных частей. Собственно, это и есть применение математики в жизни.
Если мы разделим тортик на две части, то их называют половинки, или если в виде дроби — «одна вторая».

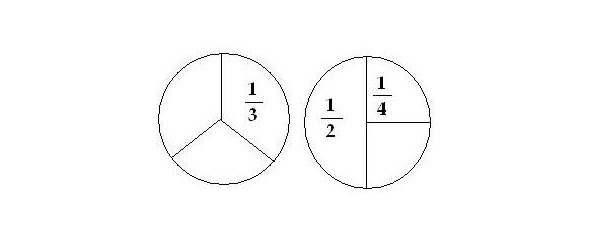
Если ученик сам не смог вспомнить — как называются числитель и знаменатель, то надо ему на них показать, назвать и попросить самому дать определения этим словам, а потом потренировать, показывая ему на примеры дробей. Эти слова часто используют в математике, физике и даже просто в жизни: вы слышали когда-нибудь — «надо их к одному знаменателю привести»? «Привести», кстати, в математике означает не «переместить к нужному пункту что-то или кого-то». Как «привести машину к подъезду». В математике «привести» — значит сделать действия в соответствии с правилами, чтобы получилось что-то одно или одинаковое с чем-то. То есть надо сделать так, чтобы у дробей были одинаковые знаменатели.
Попросите ученика разделить «тортики» (круги) на 4 равные части, на 8 частей, на 3 части. Пусть поищут способы, чтобы части были равными.
Скажите, что когда делим на 4 части, то одна из частей называется одна ЧЕТВЁРТАЯ, две таких части — две четвёртых, три — три четвертых. Пусть он попрактикуется в названии разных дробей пока не поймёт это очень хорошо.
Потом спросите — как нам сложить одинаковые части? Одна четвёртая и одна четвёртая будет сколько? Правильно — две четвёртых. То есть, если мы складываем дроби с одинаковым знаменателем — мы не трогаем знаменатели, они остаются теми же, а числители складываем. Если ученик будет складывать знаменатели (например, одна вторая и одна вторая у него будет получаться две четвёртых, а это неверно!), попросите его нарисовать на тортике — что у него получается, какие части торта и пусть он сравнит наглядно с тем, что должно получиться при правильном сложении.
Далее нам надо сложить дроби с разными знаменателями. Если у него трудности, то я объясняю, как это делается на таком примере:
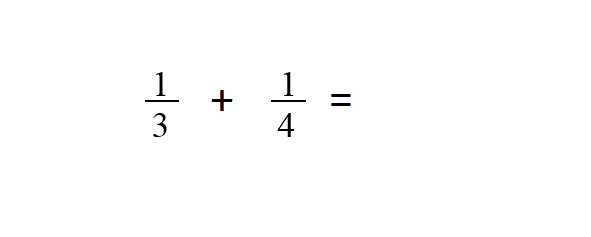
Эти части тортика — разные по величине. Их можно сдвинуть вместе, и мы получим какую-то реальную часть тортика:
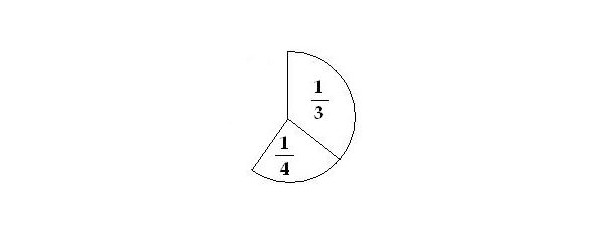
Но в числовом примере нам надо их ещё как-то записать, а для устного ответа — назвать правильными словами. Для этого нам надо разбить эти части на более мелкие, которые будут одинаковы. Например так:
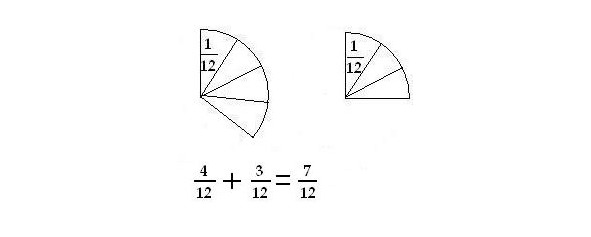
Вот в этих более мелких частях мы и запишем ответ. Если мы разделим каждую одну четвёртую на три части, а одну третью на четыре, то это будут более мелкие и одинаковые — двенадцатые части. Одна четвёртая будет состоять из трёх двенадцатых, а одна третья из четырёх двенадцатых. И вместе это будет — семь двенадцатых.
Надо потренировать ученика складывать разные дроби до уверенности. Потом те же принципы применяются при сложении дробей в алгебре в 6 классе и старше — где вместо чисел будут разные буквы и целые выражения. Но правила сложения и умножения дробей ТЕ ЖЕ самые.
Умножение дробей
Если ученик легко складывает дроби, то я перехожу к умножению дробей. Тут надо просто запомнить правило: при умножении дробей числитель умножается на числитель, а знаменатель — на знаменатель.
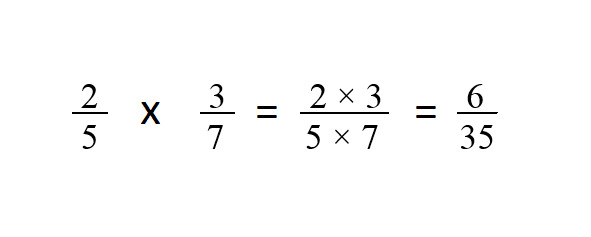
Конечно, надо до уверенности попрактиковаться в этом действии!
Деление дробей
При делении дробей можно, конечно, разделить числитель на числитель, а знаменатель на знаменатель. Но это не всегда получается — если мы в предыдущем примере попробуем разделить 2 на 3 и 5 на 7, то вряд ли получится что-то удобное. Потому делают так: вторую дробь переворачивают, и первую дробь умножают на ПЕРЕВЁРНУТУЮ вторую дробь.
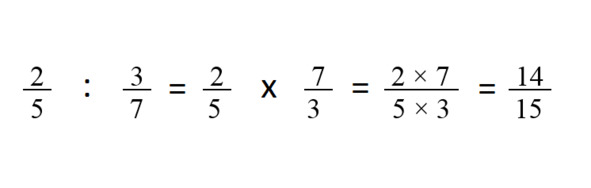
Это правило надо понять и усвоить. И, конечно, надо до уверенности попрактиковаться в этом действии!
ПРОПОРЦИИ
«Пропорцией» называют равенство двух отношений. «Отношением» в математике называют просто действие деления. То есть «2 делить на 5», также называется «отношение двух к пяти». 2: 5 — это отношение. Тогда пропорция будет 2: 5 = 4: 10, или 5: 15 = 1: 100. Первая пропорция верная, а вторая пропорция — неверная, потому что результаты деления во втором примере не одинаковы. Эти понятия надо хорошо понять и запомнить, так как они используются много в математике, физике, химии и в жизни. Придумайте несколько предложений или идей с этими понятиями, если они вам не очень знакомы.
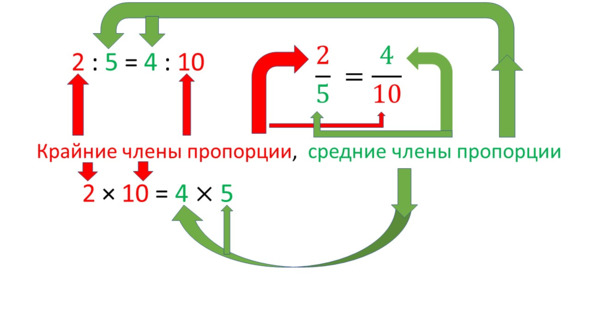
В пропорции 2: 5 = 4: 10 числа 2 и 10 называются КРАЙНИМИ членами пропорции, а 5 и 4 — средними членами пропорции, потому что 2 и 10 находятся на краях слева и справа в этой записи, а 5 и 4 — в середине записи. Для любой ВЕРНОЙ пропорции будет выполняться равенство
2 × 10 = 4 × 5
То есть: 20 = 20 — верно
Или словами: произведение крайних членов пропорции равно произведению средних членов пропорции. Это свойство применяется для облегчения решения разных задач. Так, часто может быть трудно сообразить — что надо сделать с двумя действиями деления или с двумя дробями.
Например: 25: Х = 2: 10 — тут даже супер-отличник может голову сломать, решая это уравнение. Используем свойства пропорции:
25 × 10 = 2 × Х
или 2 × Х = 25 × 10 2 × Х = 250
тогда Х = 250: 2
Х = 125 — мы нашли решение!
ПРОЦЕНТЫ
Проценты прочно вошли в нашу жизнь в банках, на работе и в магазинах. Про них надо знать и достаточно хорошо разбираться в них для успешного выживания в этом мире продаж, скидок и кредитов.
Слово «процент» — латинское, означает «делить на сто». Обозначается как %. Примеры: 5%, 20%, 156%. Родственные слова: цент — сотая часть доллара или евро, центнер — 100 кг. То есть это просто сотая часть от чего-то. 20% тортика — это если мы разделим тортик на 100 частей и возьмём 20 таких частей. То есть в виде дроби это 20 сотых, 0,20; или 20/100.
В различных задачах на проценты самое главное — понять: что же надо взять за 100%? Это обычно что-то, что является целым или главным — все деньги на какой-то момент, всё количество чего-то (все конфеты, всё молоко, весь тортик). В сложных задачах часто в первой части задачи за 100% берётся что-то одно, а потом во второй части задачи за 100% надо принимать уже что-то другое.
Есть несколько способов решения задач на проценты: можно их решать, исходя из смысла понятия «процент» и выводить формулы самому каждый раз, а можно использовать формулы механически, но тогда можно ошибаться на «каверзных» задачах.
Самый элементарный способ — это решать задачи через расчёт 1%. Например: Вася отдал в банк 1200 р. под 8% годовых. Сколько он получит через год денег из банка?
Первый способ решения: за 100% надо взять всю исходную сумму 1200 р. (всё, что было в начальный момент времени; вся сумма с которой начисляются проценты)
Тогда 1% будет 1200: 100 = 12 (рублей)
И тогда 8% будет 1% × 8 = 12 р. × 8 = 96 р.
Значит получит Вася 1200 р +96 р. = 1296 р.
Второй способ решения: через составление пропорции
вся исходная сумма 1200 р. — это 100%
через год будет неизвестная сумма Х,
которая в процентах будет равна
100% (начальных) +8% (начисленных) = 108% (через год)
Значит Х р. — это 108%
получается пропорция 1200 р: 100% = Х р: 108%
По свойству пропорции (произведение крайних членов пропорции равно произведению средних членов пропорции):
100 × Х = 1200 × 108
100 × Х = 129600
то есть Х = 129600: 100 = 1296 (р.)
Дата: 2018-12-28, просмотров: 413.