Аннотация
Для кого эта книга: для родителей, которые хотят сами улучшить знания своих детей. Для учителей и репетиторов, которые хотят получать результаты быстрее и с меньшими затратами сил и нервов. Для тех, кто хочет хорошо сдать ГИА или ЕГЭ, но не знает с чего начать.Цель этой книги: в доступной и понятной форме объяснить родителям, старшим и младшим школьникам основные понятия математики и помочь натренировать практические навыки по математике за 1—5 классы до полной уверенности.
Вся математика за 1-5 класс просто и доходчиво
Книга со ссылками на видеоролики
Игорь Владиславович Казаринов
Дизайнер обложки Наталья Павловна Яровая
© Игорь Владиславович Казаринов, 2018
© Наталья Павловна Яровая, дизайн обложки, 2018
ISBN 978-5-4493-8165-1
Создано в интеллектуальной издательской системе Ridero
Книга со ссылками на ВИДЕОРОЛИКИ
В помощь для изучения есть:
Видеоролики на моём канале Ютуба.
Сайт study.igor-kazarinov.ru. (Сайт и канал на Ютубе легко найти в любом поисковике, если набрать мои имя и фамилию «Игорь Казаринов»)
ЖЕЛАЮ УСПЕХА!
©2011,2018 Казаринов И. В. Все права защищены. Глубокая признательность выражается L. Ron Hubbard Library (библиотеке Л. Рона Хаббарда) за любезное разрешение использовать отрывки из защищённых авторскими правами работ Л. Рона Хаббарда. Applied Scholastics и знак Applied Scholastics являются торговыми марками и знаками обслуживания, принадлежащими ABLE International (Международная Ассоциация по улучшению жизни и образования) и используются только с её разрешения. Напечатано в России.
Как улучшить понимание математики и сделать математические слова «родными»
ТАБЛИЦА СЛОЖЕНИЯ
Ученики должны знать очень хорошо всю таблицу сложения. Я повторю: Ученики должны знать очень хорошо всю таблицу сложения. Это самое первое действие в математике, оно самое простое и именно поэтому надо убедиться, что ученики быстро и уверенно умеют складывать числа от 1 до 9. Если это не оттренировано (не заучено наизусть), то ученики будут ДОЛГО вычислять и часто делать обидные ошибки в сложении и вычитании. Уверенное знание сложения поможет не только в школе до самого последнего экзамена, но и очень полезно в жизни. Никому не помешает умение быстро считать.
В школах сейчас почему-то на это мало обращают внимание. Таблица сложения может висеть на стене, но почему-то её не просят ЗНАТЬ наизусть! Возможно считают, что это слишком просто и дети сами научатся. Но это просто для человека взрослого, который много лет считает в жизни, а для ребёнка, который только вчера узнал о сложении вообще это очень сложно и не знакомо. В каких-то школах в первом классе, когда надо учить таблицу сложения, не ставят оценок. А когда начинают ставить оценки – уже не учат сложение. Эта «доброта» выходит большинству учеников «боком» – не доученное вовремя будет отнимать время и нервы всю школу.
Таблица умножения
Таблицу умножения, как я уже писал раньше, знают хорошо только некоторые школьники. Обычно те, с которыми занимались дома бабушки. Эту таблицу люди придумали, чтобы облегчить себе вычисления. Умножать нам приходится в жизни довольно часто. Значит, как раз в школе даётся время для того, чтобы научится делать это быстро и без ошибок на всю жизнь. Время, потраченное на тренировку таблицы умножения, вернётся много раз в будущем. Мне часто ученики говорят: «А на калькуляторе быстрее!» Это не совсем так. Очень сложные вычисления легче сделать на машинке. А простые — быстрее в уме или на бумаге. Один раз я на спор с учеником делал его домашнее задание на вычисление. Я — на бумаге, а он решал на калькуляторе. Когда я закончил, он ещё не дошёл до середины.
Кроме этого, я задаю ученику ещё пару вопросов:
1) А что будет, если ты случайно нажмёшь не ту клавишу? (Одна ученица старших классов пересчитывала несколько раз и брала среднее между вычислениями! Интересный способ, да?)
2) Есть такие примеры и задания, которые нельзя быстро посчитать на калькуляторе. Например: на какие числа делится 60? Что вы будете делать — перебирать ВСЕ числа от 1 до 60 на калькуляторе? А зная таблицу умножения — такую задачу очень легко решить.
Поэтому для достижения хороших результатов в изучении математики и для получения хорошей и отличной оценки на экзаменах надо ЗНАТЬ таблицу умножения! Тренируется она так же, как написано для таблицы сложения, и как показано в видеоролике «Таблица умножения быстро, легко и весело выучить».
— Ученик просматривает ОДИН столбец таблицы умножения на одно число и проговаривает его вслух и громко. Если он сбивается, или ошибается, лучше ещё несколько раз просмотреть и повторить весь столбец.
— Ученика спрашивают вразброс примеры на это число. Если он отвечает без задержки, этот пример можно не тренировать. А если ошибается и задумывается, то этот пример надо тренировать до тех пор, пока ученик не станет отвечать мгновенно. Когда на все примеры для этого числа ученик отвечает так же быстро, как 2×2=4, дайте ему хорошее подтверждение и переходите к следующему столбцу. (Подтверждения надо давать после КАЖДОГО ответа на ваш вопрос. Это очень ускоряет тренировку и создаёт комфортную обстановку для ученика и для тренера.)
УМНОЖЕНИЕ ЧИСЛА НА СКОБКУ
Если число умножают на скобку, в которой складываются два других числа, то получится тоже самое, если мы умножим число на первое число в скобке и сложим это с числом, умноженным на второе число в скобке.
А× (В + С) = А×В + А×С
Это легко проверить с небольшими числами:
3× (4 +1) = 3×4 +3×1 = 12 +3 = 15
Тоже самое получится, если мы сначала сделаем действия в скобках:
3× (4 +1) = 3×5 = 15
Это правило применяется при действиях с буквами, где мы не можем сложить А и В, а также для облегчения вычислений в некоторых случаях, например:
7 × 105 = 7 × (100 +5) = 7×100 +7×5 = 700 +35 = 735
Ещё одно применение этого правила — это вынесение за скобки общего множителя. Для примера выше это будет как бы выполнение действий в обратном порядке (от правой стороны выражения мы будем переходить к левой стороне выражения от знака =), например (общие множители подчёркнуты):
25 +35 = 5×5 +5×7 = 5 × (5 +7), или для букв:
А ×В + А×С = А × (В + С),
или 5 х +5у = 5 × (х + у),
или 5х +6х = (5+6) × х = 11х
УМНОЖЕНИЕ СКОБКИ НА СКОБКУ
Умножение скобки на скобку — это чуть более сложное применение того же правила:
(А + У) × (В + С) = АВ + АС + УВ + УС,
почему так — можно проверить, если мы заменим скобку (А + У) на Х, тогда будет
Х × (В + С) = ХВ + ХС
и если теперь мы поставим вместо Х снова (А + У), то получится:
ХВ + ХС = (А + У) ×В + (А + У) ×С = АВ + УВ + АС + УС
— то есть тоже самое, что в формуле, только в другом порядке, а от перестановки слагаемых сумма не меняется.
Запишем тоже самое с числами (по правилу умножения скобок):
(2 +3) × (4 +5) = 2×4 +2×5 +3×4 +3×5 = 8 +10 +12 +15 = 45
Или сначала вычислив в скобках:
(2 +3) × (4 +5) = 5 × 9 = 45
В математике часто можно вычислить значение или решить задачу несколькими разными способами. Но если всё делать без ошибок, то ответ будет тем же самым. Главное, чтобы вы были уверены в своём решении и всё делали по правилам.
ДРОБИ И ДЕЙСТВИЯ С НИМИ
Действия с дробями проходят через всю школьную математику. В жизни мы не очень много с ними сталкиваемся, хотя постоянно слышим и говорим — половина, четверть, треть. Но на всех экзаменах будут примеры на дроби и действия с ними. Очень редкие калькуляторы помогут вам в этом. Да ещё вам сначала придётся научиться использовать такой хитрый калькулятор. Довольно часто вычисления с дробями встречаются в физике, химии и изредка в биологии.
Дроби были придуманы людьми для того, чтобы справиться с проблемой деления с остатком.
8: 2 = 4 (ровно, без остатка), а 9: 2 = 4 и остаток 1.
Дробить — значит разбивать на более мелкие части. И в математике дробь — это что-то меньше, чем целая единица. Мне нравится использовать для примера тортики. Почему-то ученики с удовольствием придумывают способы для того, чтобы разделить тортики на несколько равных частей. Собственно, это и есть применение математики в жизни.
Если мы разделим тортик на две части, то их называют половинки, или если в виде дроби — «одна вторая».

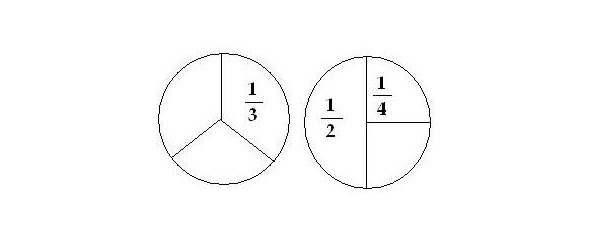
Если ученик сам не смог вспомнить — как называются числитель и знаменатель, то надо ему на них показать, назвать и попросить самому дать определения этим словам, а потом потренировать, показывая ему на примеры дробей. Эти слова часто используют в математике, физике и даже просто в жизни: вы слышали когда-нибудь — «надо их к одному знаменателю привести»? «Привести», кстати, в математике означает не «переместить к нужному пункту что-то или кого-то». Как «привести машину к подъезду». В математике «привести» — значит сделать действия в соответствии с правилами, чтобы получилось что-то одно или одинаковое с чем-то. То есть надо сделать так, чтобы у дробей были одинаковые знаменатели.
Попросите ученика разделить «тортики» (круги) на 4 равные части, на 8 частей, на 3 части. Пусть поищут способы, чтобы части были равными.
Скажите, что когда делим на 4 части, то одна из частей называется одна ЧЕТВЁРТАЯ, две таких части — две четвёртых, три — три четвертых. Пусть он попрактикуется в названии разных дробей пока не поймёт это очень хорошо.
Потом спросите — как нам сложить одинаковые части? Одна четвёртая и одна четвёртая будет сколько? Правильно — две четвёртых. То есть, если мы складываем дроби с одинаковым знаменателем — мы не трогаем знаменатели, они остаются теми же, а числители складываем. Если ученик будет складывать знаменатели (например, одна вторая и одна вторая у него будет получаться две четвёртых, а это неверно!), попросите его нарисовать на тортике — что у него получается, какие части торта и пусть он сравнит наглядно с тем, что должно получиться при правильном сложении.
Далее нам надо сложить дроби с разными знаменателями. Если у него трудности, то я объясняю, как это делается на таком примере:
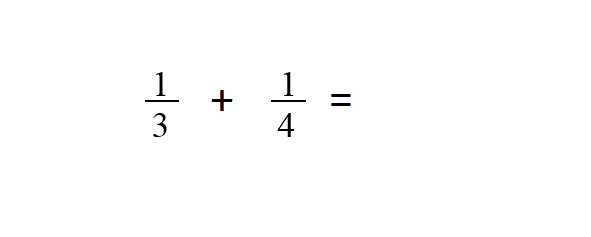
Эти части тортика — разные по величине. Их можно сдвинуть вместе, и мы получим какую-то реальную часть тортика:
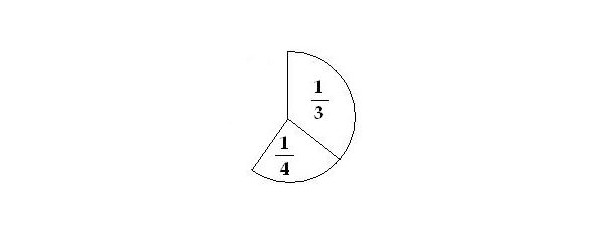
Но в числовом примере нам надо их ещё как-то записать, а для устного ответа — назвать правильными словами. Для этого нам надо разбить эти части на более мелкие, которые будут одинаковы. Например так:
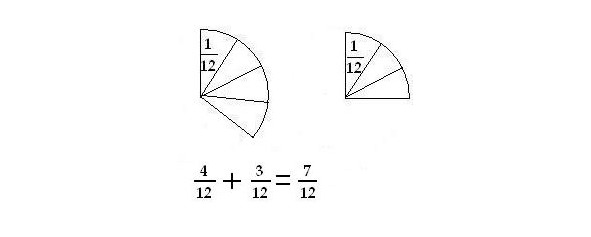
Вот в этих более мелких частях мы и запишем ответ. Если мы разделим каждую одну четвёртую на три части, а одну третью на четыре, то это будут более мелкие и одинаковые — двенадцатые части. Одна четвёртая будет состоять из трёх двенадцатых, а одна третья из четырёх двенадцатых. И вместе это будет — семь двенадцатых.
Надо потренировать ученика складывать разные дроби до уверенности. Потом те же принципы применяются при сложении дробей в алгебре в 6 классе и старше — где вместо чисел будут разные буквы и целые выражения. Но правила сложения и умножения дробей ТЕ ЖЕ самые.
Умножение дробей
Если ученик легко складывает дроби, то я перехожу к умножению дробей. Тут надо просто запомнить правило: при умножении дробей числитель умножается на числитель, а знаменатель — на знаменатель.
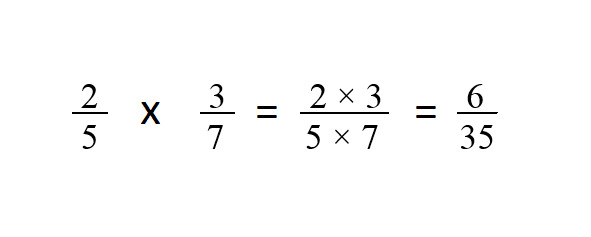
Конечно, надо до уверенности попрактиковаться в этом действии!
Деление дробей
При делении дробей можно, конечно, разделить числитель на числитель, а знаменатель на знаменатель. Но это не всегда получается — если мы в предыдущем примере попробуем разделить 2 на 3 и 5 на 7, то вряд ли получится что-то удобное. Потому делают так: вторую дробь переворачивают, и первую дробь умножают на ПЕРЕВЁРНУТУЮ вторую дробь.
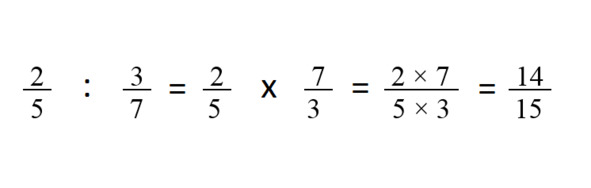
Это правило надо понять и усвоить. И, конечно, надо до уверенности попрактиковаться в этом действии!
ПРОПОРЦИИ
«Пропорцией» называют равенство двух отношений. «Отношением» в математике называют просто действие деления. То есть «2 делить на 5», также называется «отношение двух к пяти». 2: 5 — это отношение. Тогда пропорция будет 2: 5 = 4: 10, или 5: 15 = 1: 100. Первая пропорция верная, а вторая пропорция — неверная, потому что результаты деления во втором примере не одинаковы. Эти понятия надо хорошо понять и запомнить, так как они используются много в математике, физике, химии и в жизни. Придумайте несколько предложений или идей с этими понятиями, если они вам не очень знакомы.
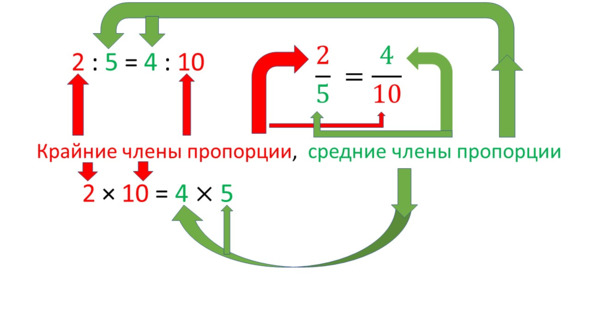
В пропорции 2: 5 = 4: 10 числа 2 и 10 называются КРАЙНИМИ членами пропорции, а 5 и 4 — средними членами пропорции, потому что 2 и 10 находятся на краях слева и справа в этой записи, а 5 и 4 — в середине записи. Для любой ВЕРНОЙ пропорции будет выполняться равенство
2 × 10 = 4 × 5
То есть: 20 = 20 — верно
Или словами: произведение крайних членов пропорции равно произведению средних членов пропорции. Это свойство применяется для облегчения решения разных задач. Так, часто может быть трудно сообразить — что надо сделать с двумя действиями деления или с двумя дробями.
Например: 25: Х = 2: 10 — тут даже супер-отличник может голову сломать, решая это уравнение. Используем свойства пропорции:
25 × 10 = 2 × Х
или 2 × Х = 25 × 10 2 × Х = 250
тогда Х = 250: 2
Х = 125 — мы нашли решение!
ПРОЦЕНТЫ
Проценты прочно вошли в нашу жизнь в банках, на работе и в магазинах. Про них надо знать и достаточно хорошо разбираться в них для успешного выживания в этом мире продаж, скидок и кредитов.
Слово «процент» — латинское, означает «делить на сто». Обозначается как %. Примеры: 5%, 20%, 156%. Родственные слова: цент — сотая часть доллара или евро, центнер — 100 кг. То есть это просто сотая часть от чего-то. 20% тортика — это если мы разделим тортик на 100 частей и возьмём 20 таких частей. То есть в виде дроби это 20 сотых, 0,20; или 20/100.
В различных задачах на проценты самое главное — понять: что же надо взять за 100%? Это обычно что-то, что является целым или главным — все деньги на какой-то момент, всё количество чего-то (все конфеты, всё молоко, весь тортик). В сложных задачах часто в первой части задачи за 100% берётся что-то одно, а потом во второй части задачи за 100% надо принимать уже что-то другое.
Есть несколько способов решения задач на проценты: можно их решать, исходя из смысла понятия «процент» и выводить формулы самому каждый раз, а можно использовать формулы механически, но тогда можно ошибаться на «каверзных» задачах.
Самый элементарный способ — это решать задачи через расчёт 1%. Например: Вася отдал в банк 1200 р. под 8% годовых. Сколько он получит через год денег из банка?
Первый способ решения: за 100% надо взять всю исходную сумму 1200 р. (всё, что было в начальный момент времени; вся сумма с которой начисляются проценты)
Тогда 1% будет 1200: 100 = 12 (рублей)
И тогда 8% будет 1% × 8 = 12 р. × 8 = 96 р.
Значит получит Вася 1200 р +96 р. = 1296 р.
Второй способ решения: через составление пропорции
вся исходная сумма 1200 р. — это 100%
через год будет неизвестная сумма Х,
которая в процентах будет равна
100% (начальных) +8% (начисленных) = 108% (через год)
Значит Х р. — это 108%
получается пропорция 1200 р: 100% = Х р: 108%
По свойству пропорции (произведение крайних членов пропорции равно произведению средних членов пропорции):
100 × Х = 1200 × 108
100 × Х = 129600
то есть Х = 129600: 100 = 1296 (р.)
СВОЙСТВА РАВЕНСТВ
Равенство — это математическая запись со знаком = «равно». Они бывают верные (3 +5 = 8) или неверные (2 +2 = 30). Для всех верных равенств можно переносить числа из правой части равенства в левую, при этом, чтобы равенство сохранялось, мы у тех чисел, которые переносим, должны поменять знак на противоположный. Например:
3 +5 = 15 — 7
То есть: 8 = 8
Перенесём 5 в правую часть равенства, а 7 — в левую. При этом мы должны поменять у них знак на противоположный. У 5 был знак +, теперь станет –. У 7 был знак –, станет +.
3 +7 = 15 — 5
Мы получим: 10 = 10
Равенство сохранилось, хотя теперь у нас результат вычислений другой. Если мы не будем менять знаки для переносимых чисел — равенство не будет сохраняться. Попробуйте убедиться сами в этом. Потренируйтесь с другими примерами в перенесениях чисел (каких захотите) из левой части равенства в правую и наоборот. Это один из главных навыков в математике, его надо усвоить очень хорошо и на всю жизнь.
УРАВНЕНИЯ
Сейчас школьников начинают учить решать уравнения иногда с первого класса. Но трудности при решении уравнений могут сохраняться до окончания школы.
В младших классах учат решать самые простые уравнения — с одной переменной. Переменная — это что-то, что может меняться. Если мы возьмём число 5 — оно не будет меняться. 5 — это всегда 5. И потому такие величины называют ещё «постоянными». Все числа — это постоянные! А величины, которые мы можем менять или которые могут меняться и принимать РАЗНЫЕ значения, называются «переменными» и обозначаются они в математике латинскими буквами. Обычно маленькими латинскими буквами, например: х, у, z, a, b и так далее.
Самые простые уравнения легко решаются, если хорошо знать таблицы сложения, умножения и правила вычислений. Например:
Х +5 = 8
Что бы равенство было верным, х должен быть равен 3. Только тогда мы получим 8, если прибавим 5 к х.
Или
5х = 25
Это будет верно, только если х = 5.
Ведь только 5 × 5 = 25.
Но есть точная последовательность действий, которую разработали математики для точного решения уравнений типа
3 +4х — 8 — 12х = 5х — 15 +9 (3х +4)
— Надо выполнить все действия, какие возможно (сложить числа друг с другом, сделать действия в скобках, если можно, или раскрыть скобки, если там нельзя сделать действия).
3 — 8 +4х — 12х = 5х — 15 +9 × 3х +9 × 4
— 5 — 8х = 5х — 15 +27х +36
— 5 — 8х = 32х +21
— Теперь надо перенести все переменные в левую сторону от знака равенства, а все числа — в правую. При этом мы применяем правила переноса через знак равенства — меняем знаки у тех чисел, которые переносим, на противоположные. (В школе я сам старался записывать сначала те величины, которые ОСТАЛИСЬ на той же части равенства и не поменяли знаки, а потом записывал те величины, которые перенёс (с изменёнными знаками). Но это просто ещё одно правило, которое помогает уменьшать число ошибок и облегчает проверку.)
— 8х — 32х = 21 +5
3) Приводим подобные. («Приводим подобные» — это математический термин. Означает, что надо выполнить действия с похожими слагаемыми. Подобными будут все числа (3, 5, 32, 184 — это всё подобные), а также слагаемые в которых одинаковая буквенная часть (5х, х, 32х — это подобные. Вот более сложные: 4abz, abz, 12abz — это тоже подобные, а 5х и 5у — это НЕ подобные — у них РАЗНЫЕ буквенные части). Надо хорошо понимать — что значит «привести подобные» и уметь выполнять это действие. Это ПОСТОЯННО используется в математике. И эти слова математики часто говорят.
— 40х = 26
4) Теперь мы получили простое уравнение. Х — здесь множитель. Как мы находим неизвестный множитель? Мы делим произведение на известный множитель.
Х = 26: (–40)
И ответ: Х = — 26/40
Этот ответ немного странно выглядит, но уравнение было взято для примера. Вы можете сами составить похожие уравнения для тренировок правильного порядка действий. Главное — чтобы ученик выполнял все действия уверенно. Если результат кажется вам странным — проверьте все действия. Но вот что никогда не надо делать — это ПОДГОНЯТЬ ваш ответ под что-то «красивое», или под ответ соседа, или под ответ в книжке. «Красиво» — не всегда правильно, сосед может ошибиться, и даже в учебниках бывают опечатки.
ДОПОЛНИТЕЛЬНЫЕ НАВЫКИ
Нахождение наибольшего общего делителя (НОД)
Для этого нужно уметь раскладывать на простые множители или находить множители в уме за счёт сообразительности. Принцип нахождения наибольшего общего делителя описан в учебниках 3—4 класса, но так как учебники обычно сдают, то я его кратко опишу:
1) У нас есть два числа. Например: 72 и 630. Надо найти их наибольший делитель. Эти числа надо разложить на простые множители. (Это было сделано в предыдущей главе).
72 = 2 × 2 × 2 × 3 × 3,
630 = 2 × 3 × 3 × 5 × 7
2) сравниваем множители, из которых состоят первое и второе число, выбираем такие множители, какие встречаются в обоих числах. Мы видим, что в оба разложения содержат 2 и 3, а значит они оба делятся на 2 и на 3. Итак, 2 и 3 — это делители этих чисел.
3) Так как мы ищем НАИБОЛЬШИЙ делитель, то нам надо найти все ОДИНАКОВЫЕ делители, в том числе повторяющиеся. Одинаковыми делителями в нашем случае будут 2, 3, 3. (Хотя 2 встречается в 72 три раза, мы берём её один раз, так как 2 только один раз входит в число 630.) Тогда НАИБОЛЬШИМ общим делителем будет произведение всех общих делителей:
2 × 3 × 3 = 18.
18 — наибольший общий делитель для 72 и 630.
4) можно проверить, что эти числа делятся на 18:
72: 18 = 4, 630: 18 = 35.
ТАБЛИЦЫ ДЛЯ ЗАУЧИВАНИЯ
Таблица сложения

Таблица вычитания

Таблица умножения

Таблица деления

ПРО АВТОРА
Меня зовут Игорь Владиславович Казаринов. Я лицензированный профессиональный репетитор «Прикладного образования». («Прикладное образование» — международная некоммерческая организация, цель которой — сделать открытия американского исследователя Л. Рона Хаббарда в области обучения известными во всём мире с целью повысить уровень образования обучающихся).
В школе я решал все контрольные за 20 минут. Занимал призовые места в олимпиадах по математике, физике и химии. Но я не знал, почему я могу так учится, а другие не могут.
Учителя в школах, преподаватели в ВУЗах и репетиторы тогда не знали, и сейчас тоже (большинство, по крайней мере) этого не знают.
К огромному сожалению!
У меня были разные учителя — и хорошие, и самые лучшие! Они прекрасно разбирались в предметах. Но, при всём этом, мы все учились кто как умел. У меня была хорошая способность учиться. У кого-то она была гораздо хуже… И прекрасные учителя-предметники НИКАК не могли эту способность улучшить — ни у меня, ни у двоечников. Единственный совет был и остаётся: «Учите!».
Как же надо учить?
У меня есть младшая сестра. В школе у неё были трудности с математикой. И я пытался ей помочь. Но получалось только помочь ей сделать «домашку». Как только я переставал ей помогать разбираться с задачами — её оценки по математике сразу падали.
Это отсутствие стабильных результатов мне довольно быстро надоело. Сестре отличная оценка по математике была не очень нужна, а тройку у нас в школе всегда найдут за что поставить — всех же на второй год не оставишь!
Одно время у меня была мысль после школы стать учителем математики, раз у меня так хорошо получается с ней разбираться. Но неудачный опыт помощи сестре и многолетние наблюдения за тем, как учителя на уроках пытаются безуспешно справиться с непониманием математики (совершенно мне ясной!) у 85% процентов учеников, привели к тому, что я отказался от идеи стать учителем.
Я закончил ФМШ при НГУ (Физико-математическую школу-интернат при Новосибирском государственном университете) и НГУ (Новосибирский государственный университет) и работал в Институте органической химии Сибирского отделения Академии Наук СССР.
Такие предметы, как математика, физика и химия мне хорошо понятны и знакомы. Но при этом у меня не было идеи использовать свои знания и навыки для работы преподавателем или репетитором. Я не знал — почему кто-то другой не может понять элементарные вещи.
Я не мог исправить чужое непонимание. Иногда у меня самого не получалось с чем-то разобраться во время обучения в университете, и я шёл на экзамен или зачёт с надеждой, что трудную тему не спросят. Конечно, такие вещи не добавляли мне уверенности в своих способностях.
Понятно, что с неуверенными знаниями невозможно работать и получать хорошие результаты.
Мне повезло, что пробелов было не очень много — это раз. Во-вторых, на практике оказалось, что о-очень много сложных тем не имеют никакого отношения к повседневной работе даже в академическом институте, не говоря уже о работе инженера-технолога на предприятии.
Позже, начав работать репетитором и вновь открыв школьные учебники, я с удивлением обнаружил, что там очень много данных и формул из университетских курсов. А на первом курсе очень многие вещи были отлично знакомы по школе. В практической работе мне бы вполне хватило уверенного владения школьными знаниями, которые дополнились бы специальными знаниями, которые всё равно не давали в университете.
А большую часть университетских знаний я никогда-никогда не использовал, и у меня даже не возникало повода пожалеть о том, что я что-то недопонял во время учёбы.
Выходило, что я зря потратил 5 лет на учёбу в прекрасном университете!
Ведь я достаточно хорошо усвоил школьную программу.
Для меня ситуация изменилась, когда я познакомился с самыми современными открытиями в области обучения и разработанной на основе этих открытий технологией обучения (Технология обучения — это точные данные и методы, позволяющие изучить любой предмет максимально быстро и без негативных последствий).
Эти открытия были сделаны американским исследователем и философом Л. Роном Хаббардом. К настоящему моменту есть много специальных центров, а также репетиторов, применяющих эту технологию. С их помощью миллионы людей во всём мире знакомятся с этими открытиями и начинают применять их в своей жизни, изучая что угодно. Я один из этих репетиторов. Теперь я знаю точную причину трудностей и могу очень быстро найти истоки непонимания и эффективно исправить эту ситуацию. Я значительно поднял свою собственную способность учиться!
Узнав причины проблем, я потратил определённое время, чтобы разобраться со своим прошлыми пробелами. В результате у меня неожиданно значительно улучшилось настроение вообще и вырос энтузиазм по отношению к моим текущим делам. Я стал физически чувствовать себя лучше и практически перестал болеть.
Так как я продолжаю постоянно изучать что-то новое, что необходимо для моей работы, я всегда применяю технологию обучения в своей собственной учёбе. Поэтому я очень хорошо усваиваю данные и учусь быстрее большинства людей. При этом я понимаю гораздо больше, чем «быстрые» зубрилы, которые могут наизусть пересказать целую главу. Однако, когда пробуют применить изученное на практике — не всегда могут получить результат.
Теперь я могу улучшить способность учиться у любого ученика. И ученикам нравится заниматься со мной. Они получают результаты, на которые уже не надеялись в школе. Мне нравится слышать, когда они говорят: «Математика — это просто!» Действительно, это просто, когда ты её понимаешь!
Приведу лишь несколько отзывов:
«Большое, большое спасибо! Я очень многое смогла понять всего лишь за 2 часа. Это ЗДОРОВО!!!!! Спасибо!»
Эльмира У., математика, 7 класс.
«На первом занятии я разобралась с формулами, поняла, как решать задачи, которые для меня были непонятны».
Дарья Г., математика
«За 4 часа занятий по алгебре я усвоила материал, который практически не понимала раньше. Повторила забытый, но очень важный материал. И узнала много новых способов решения выражений. Огромное спасибо!»
Алиса Н., 8 класс.
«Я узнал новый метод изучения математики. Он является очень простым и понятным способом».
Юрий Д., 8 класс.
Больше отзывов можно прочитать на моём сайте: http://study.igor-kazarinov.ru
Сейчас я обращаю внимание на те моменты, на которые, к сожалению, не смотрят преподаватели и репетиторы, которые не знакомы с технологией обучения.
Поэтому, во время занятий, я не повторяю одно и то же разными словами, а разматываю клубок непонимания, который часто завязывался с первого класса.
Ведь если его не распутать, а продолжать наматывать — результатом будут истерики ребёнка, родителей и учителей, скандалы, крики и прочий негатив. Или слабые результаты, не сравнимые с затратами времени, сил и средств (в том числе материальных — на оплату репетиторов и разных дополнительных курсов уходят вполне приличные средства!).
Сейчас и школьники, и родители, и преподаватели, и студенты могут в «Прикладном Образовании» получить те же знания, которые получил когда-то я. Они могут научиться применять Технологию обучения в своей жизни и учёбе. Освоив Технологию обучения, они могут стать знающими и успешными профессионалами в деле, которое им нравится и которым они хотят заниматься.
Я уверен, что вы найдёте в моих книге и на сайте http://study.igor-kazarinov.ruответы на многие вопросы по проблемам обучения и образования.
Вы всегда можете обратиться ко мне за консультацией. Вводная консультация предоставляется БЕСПЛАТНО.
Меня так же можно найти в социальных сетях — Фэйсбуке, ВКонтакте.
Аннотация
Для кого эта книга: для родителей, которые хотят сами улучшить знания своих детей. Для учителей и репетиторов, которые хотят получать результаты быстрее и с меньшими затратами сил и нервов. Для тех, кто хочет хорошо сдать ГИА или ЕГЭ, но не знает с чего начать.Цель этой книги: в доступной и понятной форме объяснить родителям, старшим и младшим школьникам основные понятия математики и помочь натренировать практические навыки по математике за 1—5 классы до полной уверенности.
Вся математика за 1-5 класс просто и доходчиво
Дата: 2018-12-28, просмотров: 730.