Построение нелинейной регрессии с использованием команды «Добавить линию тренда»
Решение: Команда «Добавить линию тренда» используется для выделения тренда (медленных изменений) при анализе временных рядов. Однако эту команду можно использовать и для построения уравнения нелинейной регрессии, рассматривая в качестве времени  независимую переменную
независимую переменную 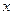 .
.
Эта команда позволяет построить следующие уравнения регрессии:
· линейную 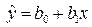
· полиноминальную 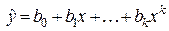 (
( 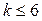 );
);
· логарифмическую 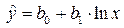
· степенную 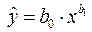 ;
;
· экспоненциальную 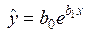 .
.
Для построения одной из перечисленных регрессий необходимо выполнить следующие шаги:
- В выбранном листе Excel ввести по столбцам исходные данные 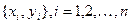
- По этим данным построить точечный график в декартовый системе координат
- Установить курсор на построенном графике, сделать щелчок правой кнопкой и в появившемся контекстном меню выполнить команду Добавить линию тренда.
- В появившемся диалоговом окне активизировать закладку «Тип» и выбрать нужное уравнение регрессии.
- Активизировать закладку «Параметры» и «включить» необходимые для нас опции:
Ö «Показать уравнение на диаграмме» - на диаграмме будет показано выбранное уравнение регрессии с вычисленным коэффициентами;
Ö «Поместить на диаграмму величину достоверности аппроксимации ( R ^2)» - на диаграмме будет показана значение коэффициент детерминации 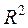 (для нелинейной регрессии -индекс детерминации). Если по построенному уравнению регрессии необходимо выполнить прогноз, то нужно указать число периодов прогноза.
(для нелинейной регрессии -индекс детерминации). Если по построенному уравнению регрессии необходимо выполнить прогноз, то нужно указать число периодов прогноза.
После задания всех перечисленных опций щелкнуть на кнопке «OK» и на диаграмме появиться формула построенного уравнения регрессии и значение индекса детерминации 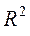 .
.
Сравните результаты полученные на графиках линий тренда с расчетными
Например, для логарифмической модели получим следующий результат (Рисунок 2 ).
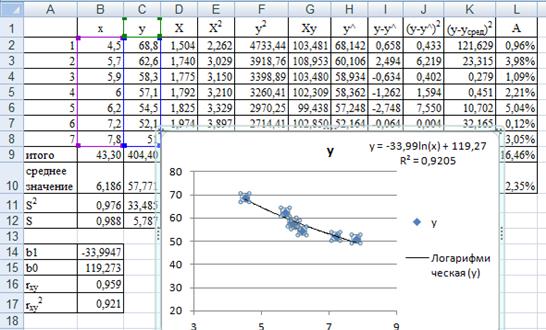
Рисунок 2 – Построение линии тренда для логарифмической модели.
Расчет параметров для экспоненциальной и логарифмической моделей можно выполнить самостоятельно.
Для построения уравнения экспоненциальной кривой у = а · еbх линеризуем переменные логарифмированием обеих частей уравнения:
ln у = ln а + b·x получим линейное уравнением Y = A + b·x
Где Y = ln y, A = ln a. После определения коэффициентов необходимо сделать обратную замену a=eA.
Для логарифмической функции вида y=a+b·ln x вводится замена X=ln x. Дальнейшие вычисления аналогичны гиперболической функции.
Ниже в таблице 3 приведены сводные характеристики построенных моделей:
Таблица 3 - Сводные характеристики построенных моделей:
| Параметры Модели | Уравнение | Коэффициент детерминации R2 | Средняя относительная ошибка аппроксимации А |
| Линейная | 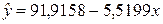
| 0,8876 | 2,99%, |
| Гиперболическая | 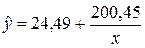
| 0,934 | 1,86% |
| Степенная | ŷ = 162,768 x-0,575 | 0,931 | 2,02%. |
| Экспоненциальная | ŷ = 102,73e-0,0938x | 0,908 | 2,65% |
| Логарифмическая | 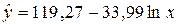
| 0,921 | 2,35% |
Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов. Чем ближе R2 к 1, тем выше качество модели. Из таблицы видно, что таким уравнением является гиперболическая функции.
При сравнении моделей по данным характеристикам мы видим, что наибольшее значение коэффициента детерминации R2 и наименьшую ошибку аппроксимации имеет гиперболическая модель, следовательно, ее можно считать лучшей.
Для вычисления y в точке x=10 используем уравнение 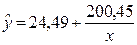 . Получим y=44,536.
. Получим y=44,536.
В системе MathCAD существуют встроенные функции для вычисления коэффициентов а и b линейной зависимости y = ax + b:
- slope(x,y) - возвращает значение коэффициента а;
- intercept(x,y) - возвращает значение коэффициента b.
Формулы для вычисления коэффициентов а и b линейной зависимости можно применять для нахождения параметров эмпирических функций, график которых не является прямой линией.
Пример 4. Решение задачи обработки экспериментальных данных в MathCAD.
|
|
| Линейная функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Степенная функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Показательная (экспоненциальная) функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Логарифмическая функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Гиперболическая функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
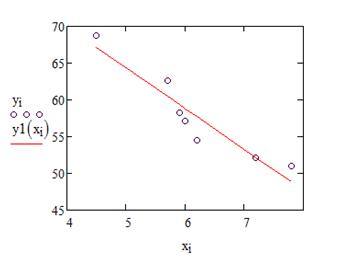
Рисунок 18 – График линейной функции
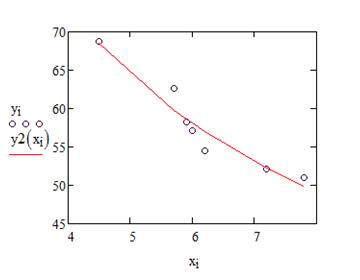
Рисунок 19 – График степенной функции
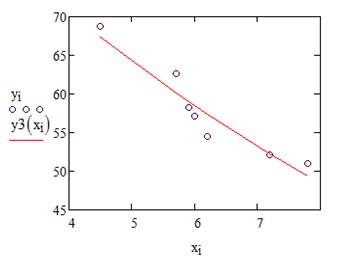
Рисунок 20 – График экспоненциальной функции
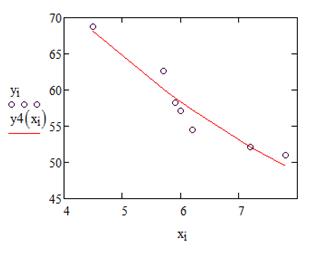
Рисунок 21 – График логарифмической функции
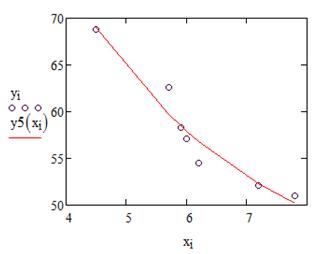
Рисунок 21 – График гиперболической функции
Видим, что в данном примере все функции неплохо описывают исходную зависимость, однако, наилучшей является гиперболическая регрессионная модель.
ПРиложение Б
Данные для построения графиков
Вариант 1
| x | 0.1 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
| y | 3.0 | 4.38 | 6.78 | 9.86 | 14.96 | 22.07 | 33.17 | 49.23 |
Вариант 2
| x | 0.05 | 0.2 | 0.4 | 0.6 | 0.9 | 1.2 | 1.5 | 1.8 |
| y | 0.521 | 1.555 | 3.572 | 5.622 | 7.801 | 11.77 | 14.78 | 17.82 |
Вариант 3
| x | 0.1 | 0.2 | 0.5 | 0.7 | 1 | 1.2 | 1.5 | 2.5 |
| y | 3.02 | 4.38 | 6.78 | 9.86 | 14.96 | 22.07 | 33.17 | 49.23 |
Вариант 4
| x | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 2.0 | 3.0 | 4.0 |
| y | 11.213 | 8.0617 | 6.3512 | 4.8412 | 4.1201 | 0.9103 | 0.5413 | 0.1512 |
Вариант 5
| x | 0.1 | 0.5 | 1 | 1.7 | 2.50 | 3.5 | 5 | 6 |
| y | 109.13 | 40.271 | 14.728 | 5.5432 | 2.1201 | 0.8403 | 0.1733 | 0.2112 |
Вариант 6
| x | 0.2 | 0.45 | 0.6 | 0.8 | 1.0 | 3.0 | 5.0 | 7.0 |
| y | 4.455 | 9.034 | 9.952 | 11.38 | 12.52 | 17.98 | 20.55 | 22.23 |
Вариант 7
| x | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 2.0 | 4.0 | 6.0 |
| y | 6.733 | 4.027 | 1.762 | 1.452 | 1.211 | 0.693 | 0.423 | 0.312 |
Вариант 8
| x | 8.0 | 6.0 | 4.0 | 2.0 | 1.0 | 0.8 | 0.6 | 0.4 |
| y | 0.2813 | 0.6123 | 0.6512 | 1.6122 | 2.9201 | 3.8503 | 4.9123 | 7.6212 |
Вариант 9
| x | 0.05 | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 | 12.0 | 14.0 |
| y | 0.0121 | 2.7312 | 4.1012 | 4.8112 | 5.7601 | 6.2203 | 7.0313 | 7.5812 |
Вариант 10
| x | 0.2 | 0.45 | 0.6 | 0.8 | 1.0 | 3.0 | 5.0 | 7.0 |
| y | 5.121 | 5.531 | 5.642 | 5.95 | 6.11 | 9.13 | 13.53 | 20.31 |
Вариант 11
| x | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 3.0 | 5.0 | 7.0 |
| y | 17.23 | 19.11 | 19.52 | 20.03 | 20.52 | 22.67 | 23.73 | 24.55 |
Вариант 12
| x | 0.2 | 0.45 | 0.9 | 1.5 | 3.0 | 5.0 | 7.0 | 10 |
| y | -2.323 | -0.727 | -0.122 | 0.6582 | 0.9001 | 3.3103 | 4.1213 | 4.9812 |
Приложение B – Расчет параметров линейной парной регрессии с помощью пакета Анализа данных
| ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| Регрессионная статистика |
|
|
|
|
|
|
| ||
| Множественный R | 0,9422 |
|
|
|
|
|
|
| |
| R-квадрат | 0,8876 |
|
|
|
|
|
|
| |
| Нормированный R-квадрат | 0,8652 |
|
|
|
|
|
|
| |
| Стандартная ошибка | 2,2950 |
|
|
|
|
|
|
| |
| Наблюдения | 7,0000 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| Дисперсионный анализ |
|
|
|
|
|
|
|
| |
|
| df | SS | MS | F | Значимость F |
|
|
| |
| Регрессия | 1,0000 | 208,0598 | 208,0598 | 39,5034 | 0,0015 |
|
|
| |
| Остаток | 5,0000 | 26,3344 | 5,2669 |
|
|
|
|
| |
| Итого | 6,0000 | 234,3943 |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
|
| Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | |
| Y-пересечение | 91,9158 | 5,5013 | 16,7079 | 0,0000 | 77,7742 | 106,0574 | 77,7742 | 106,0574 | |
| x | -5,5199 | 0,8782 | -6,2852 | 0,0015 | -7,7775 | -3,2623 | -7,7775 | -3,2623 | |
|
|
|
|
|
|
|
|
|
| |
| ВЫВОД ОСТАТКА |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| Наблюдение | Предсказанное y | Остатки |
|
|
|
|
|
| |
| 1 | 67,0764 | 1,7236 |
|
|
|
|
|
| |
| 2 | 60,4525 | 2,1475 |
|
|
|
|
|
| |
| 3 | 59,3485 | -1,0485 |
|
|
|
|
|
| |
| 4 | 57,6926 | -3,1926 |
|
|
|
|
|
| |
| 5 | 58,7965 | -1,6965 |
|
|
|
|
|
| |
| 6 | 52,1727 | -0,0727 |
|
|
|
|
|
| |
| 7 | 48,8608 | 2,1392 |
|
|
|
|
|
| |
Дата: 2018-12-28, просмотров: 362.
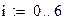
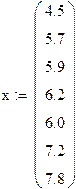
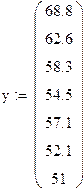
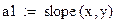
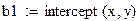
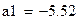
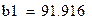
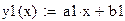
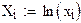
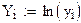
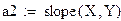
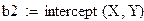
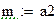
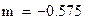
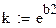
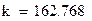
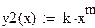
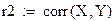
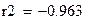
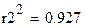
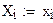
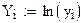
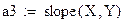
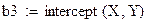
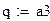
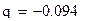
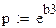
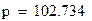
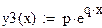
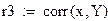
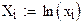
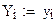
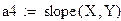
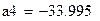
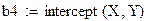
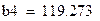
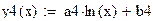
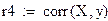
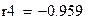
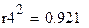
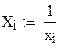
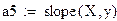
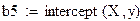
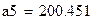
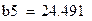
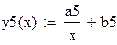
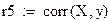
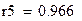
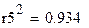
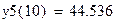
 Коэффициенты
Коэффициенты