Составить математическую модель и решить задачу линейного программирования, программу MathCad.
Задание 1. На швейной фабрике для изготовления четырех видов изделий может быть использована ткань трех артикулов. Нормы расхода тканей всех артикулов на пошив одного изделия приведены в таблице 1. В ней же указаны имеющееся в распоряжении фабрики общее количество тканей каждого артикула и цена одного изделия данного вида.
Определить, сколько изделий каждого вида должна произвести фабрика, чтобы стоимость изготовленной продукции была максимальной.
Таблица 1 - Исходные данные
| Артикул ткани | Норма расхода ткани (м) на одно изделие | Общее количество ткани (м) | |||
| изделие 1 | изделие 2 | изделие 3 | изделие 4 | ||
| I | 1 | - | 2 | 1 | 180 |
| II | - | 1 | 3 | 2 | 210 |
| III | 4 | 2 | - | 4 | 800 |
| минимальный выпуск | - | - | 10 | - | |
| максимальный выпуск | - | 200 | - | - | |
| Цена одного изделия (руб) | 9 | 6 | 4 | 7 | |
Для составления математической модели задачи обозначим:
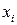 – количество изделий i -го вида, тогда
– количество изделий i -го вида, тогда
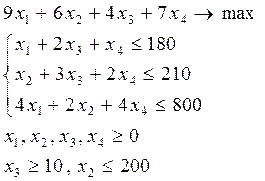
Для решения задачи в системе MathCad необходимо при описании целевой функции и ввода начальных приближений использовать знак присваивания «:=».
Далее для решения задачи используют блок функций Given … Maximize:
- ввести служебное слово Given;
- ввести систему ограничений и граничные значения;
- ввести вектор-столбец искомых параметров, знак присваивания, функцию Maximize (для задачи на минимум: Minimize) с искомыми параметрами;
- ввести вектор-столбец искомых параметров и знак «=».
Пример решения задачи 1 представлен на рисунке 1.

Рисунок 1 - Решение задачи линейного программирования в MahtCad
Задание 2.
Решить задачу линейного программирования в MathCad.
Для изготовления двух видов продукции А и В используются три вида сырья I, II, III. Ресурсы сырья, нормы его расхода на единицу продукции и получаемая прибыль от единицы продукции заданы в следующей таблице 4:
Таблица 2 – Расчетные данные
| Сырье | Нормы расхода | Ресурсы | |
| А | В | ||
| I | А1 | А2 | В1 |
| II | А3 | А4 | В2 |
| III | А5 | А6 | В3 |
| Прибыль | С1 | С2 | |
Определить оптимальный план выпуска продукции из условия максимизации прибыли.
Данные по вариантам берутся из таблицы 3.
Таблица 3 – Данные для таблицы 2
| № | A1 | A2 | A3 | A4 | A5 | A6 | B1 | B2 | B3 | C1 | C2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 1 | 7 | 3 | 5 | 5 | 2 | 60 | 45 | 20 | 20 | 50 |
| 2 | 1 | 7 | 3 | 5 | 5 | 2 | 70 | 90 | 40 | 20 | 40 |
| 3 | 1 | 7 | 3 | 5 | 5 | 2 | 70 | 50 | 40 | 40 | 20 |
| 4 | 1 | 7 | 3 | 5 | 5 | 2 | 50 | 50 | 40 | 40 | 20 |
| 5 | 1 | 7 | 3 | 5 | 5 | 2 | 15 | 40 | 50 | 50 | 50 |
| 6 | 3 | 2 | 4 | 2 | 2 | 3 | 50 | 70 | 60 | 50 | 40 |
| 7 | 3 | 2 | 4 | 2 | 2 | 3 | 50 | 50 | 60 | 60 | 40 |
| 8 | 3 | 2 | 4 | 2 | 2 | 3 | 40 | 45 | 60 | 60 | 40 |
| 9 | 3 | 2 | 4 | 2 | 2 | 3 | 50 | 45 | 60 | 40 | 50 |
| 10 | 3 | 2 | 4 | 2 | 2 | 3 | 50 | 90 | 60 | 40 | 50 |
| 11 | 2 | 3 | 4 | 1 | 2 | 1 | 50 | 100 | 30 | 50 | 30 |
| 12 | 2 | 3 | 4 | 1 | 2 | 1 | 50 | 40 | 30 | 50 | 40 |
Дата: 2018-12-28, просмотров: 769.