Аппроксимация функций
Орел 2018
ЛАБОРАТОРНАЯ РАБОТА № 1. Основы работы в системе MathCAD. Работа с матрицами. Построение графиков.
Документ программы MathCad называется рабочим листом. Он содержит объекты: формулы и текстовые блоки.В ходе расчетов формулы обрабатываются последовательно, слева направо и сверху вниз, а текстовые блоки игнорируются.
Ввод информации осуществляется в месте расположения курсора. Программа MathCad использует три вида курсоров. Если ни один объект не выбран, используется крестообразный курсор, определяющий место создания следующего объекта. При вводе формул используется уголковый курсор, указывающий текущий элемент выражения. При вводе данных в текстовый блок применяется текстовый курсор ввиде вертикальной черты.
Ввод формул
Формулы — основные объекты рабочего листа. Новый объект по умолчанию является формулой.
Элементы формул можно вводить с клавиатуры или с помощью специальных панелей управления. Панели управления (рисунок 1) открывают с помощью меню View (Вид) или кнопками панели управления Math (Математика). Для ввода элементов формул предназначены следующие панели:
° панель управления Arithmetic (Арифметика) для ввода чисел, знаков типичных математических операций и наиболее часто употребляемых стандартных функций;
° панель управления Evaluation (Оценка) для ввода операторов вычисления и знаков логических операций;
° панель управления Graph (График) для построения графиков;
° панель управления Matrix (Матрица) для ввода векторов и матриц и задания матричных операций;
° панель управления Calculus (Подсчет) для задания операций, относящихся к математическому анализу;
° панель управления Greek (Греческий) для ввода греческих букв (их можно также вводить с клавиатуры, если сразу после ввода соответствующего латинского символа нажимать сочетание клавиш CTRL+G, например [W][CTRL+G]-W);
° панель управления Symbolic (Символьный) для управления аналити-ческими преобразованиями.
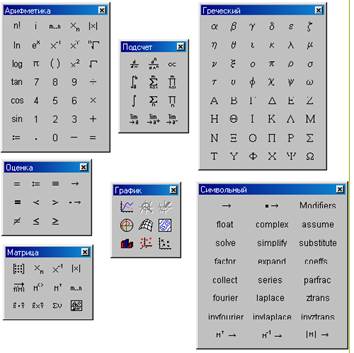
Рисунок 1 - Панели инструментов программы MathCad
Чтобы начать ввод формулы, надо установить крестообразный курсор в нужное место и начать ввод букв, цифр, знаков операций. При этом создается область формулы, в которой появляется уголковый курсор, охватывающий текущий элемент формулы, например имя переменной (функции) или число. При вводе бинарного оператора по другую сторону знака операции автоматически появляется заполнитель в виде черного прямоугольника. В это место вводят очередной операнд.
Для управления порядком операций используют скобки, которые можно вводить вручную. Уголковый курсор позволяет автоматизировать такие действия. Чтобы выделить элементы формулы, которые в рамках операции должны рассматриваться как единое целое, используют клавишу ПРОБЕЛ. При каждом ее нажатии уголковый курсор «расширяется», охватывая элементы формулы.После ввода знака операции элементы в пределах уголкового курсора автоматически заключаются в скобки.
Например, для ввода формулы 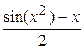 необходимо набрать
необходимо набрать 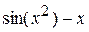
 затем нажать пробел и ввести
затем нажать пробел и ввести 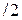 . Для ввода формулы
. Для ввода формулы 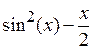 , записать
, записать 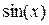 нажать пробел, чтобы уголковый курсор выделил всю формулу, возвести в степень, снова нажать пробел, а затем ввести
нажать пробел, чтобы уголковый курсор выделил всю формулу, возвести в степень, снова нажать пробел, а затем ввести 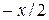 .
.
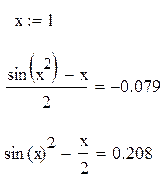
Введенное выражение обычно вычисляют или присваивают переменной. Для вывода результата выражения используют знак вычисления, который выглядит как знак равенства и вводится при помощи кнопки EvaluateExpression (Вычислить выражение) на панели инструментов Evaluation (Счет).
Знак присваивания изображается как «:=», а вводится при помощи кнопки AssignValue (Присвоить значение) на панели инструментов Evaluation (Счет). Слева от знака присваивания указывают имя переменной. Оно может содержать латинские и греческие буквы, цифры, символы «’», «_», а также описательный индекс. Последний вводится с помощью символа «.» и изображается как нижний индекс, но является частью имени переменной, например Vmin. Индексы, определяющие отдельный элемент вектора или матрицы, задаются по-другому, с помощью символа «[».
Переменную, которой присвоено значение, можно использовать далее в документе в вычисляемых выражениях. Чтобы узнать значение переменной, следует использовать оператор вычисления.
В следующем примере вычислена площадь круга с радиусом 2 (использованы переменные r и s, значение постоянной p определено в программе MathCad по умолчанию)

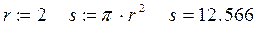
При изменении какой-либо формулы программа MathCad автоматически производит необходимые вычисления, обновляя изменившиеся значения и графики.
Ввод текста
Текст, помещенный в рабочий лист, содержит комментарии и описания и предназначен для ознакомления, а не для использования в расчетах. Текстовый блок создается нажатием кнопки с буквой А на панели инструментов или с помощью команды Insert>TextRegion (Вставка > Текстовый блок).
Иногда требуется встроить формулу внутрь текстового блока. Для этого служит команда Insert>MathRegion (Вставка > Формула).
Работа с матрицами
Векторы и матрицы рассматриваются в программе MathCad как одномерные и двумерные массивы данных. Число строк и столбцов матрицы задается в диалоговом окне InsertMatrix (Вставка матрицы), которое открывают командой Insert>Matrix (Вставка > Матрица). Вектор задается как матрица, имеющая один столбец.
После щелчка на кнопке ОК в формулу вставляется матрица, содержащая вместо элементов заполнители. Вместо каждого заполнителя надо вставить число, переменную или выражение.
При работе с матрицами приходится применять такие операции, как сложение матриц, умножение, транспонирование. Часто возникает необходимость в обращении матриц и в декомпозиции (разложении в произведение матриц специального вида). Программа MathCad позволяет выполнить все эти операции с помощью стандартных математических операторов (сложение, умножение) или встроенных функций.
Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля. Для переопределения начала нумерации используют встроенную переменную ORIGIN. Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Subscript (Индекс) на панели инструментов Matrix (Матрица).
Пара индексов, определяющих элемент матрицы, разделяется запятой. Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки, например М. Для его ввода используется кнопка MatrixColumn (Столбец) на панели инструментов Matrix (Матрица).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы задать общую формулу элементов матрицы, типа М i , j := i + j , используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента, через запятую значение второго и через две точки (используется кнопка 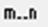 на панели Матрица) значение последнего элемента. Диапазон можно использовать как значение переменной, например x:=0,0.01..1.
на панели Матрица) значение последнего элемента. Диапазон можно использовать как значение переменной, например x:=0,0.01..1.
Если разность прогрессии равна единице (то есть элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают. Например, чтобы сформировать по приведенной выше формуле матрицу размером 4х4, перед этой формулой надо указать i:=0..3 j:=0..3.
При формировании матрицы путем присвоения значений ее элементам размеры матрицы можно не задавать заранее. Всем неопределенным элементам автоматически присваиваются нулевые значения. Например, формула М3,3:= 1 создает матрицу М размером 4х4, у которой все элементы, кроме расположенного в правом нижнем углу, равны нулю.
Символьные вычисления
В отличие от численного вычисления результатом символьного вычисления (преобразования) является формула или число, которое нельзя получить за конечное число вычислительных операций.
В Mathcad указанием к численному вычислению является знак равенства, а к символьному преобразованию стрелка вправо.
Численные вычисления:
Вычислить интеграл
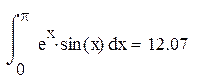
Найти сумму десяти членов ряда 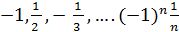
|
|
|
|
Символьные вычисления:
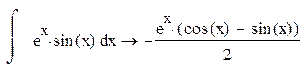
Найти производную
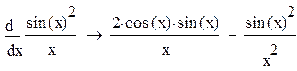
Задание 1. Вычислить значения переменных по заданным значениям исходных данных и расчётным формулам.
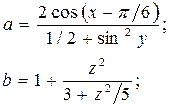 |
Вариант 1 x = 1,426
у = -1,220
z = 3,5
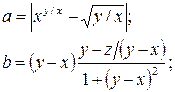 Вариант 2 x = 1,825
Вариант 2 x = 1,825
у = 18,225
z = -3,298
Вариант 3 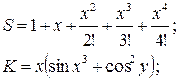
x = 0,335
у = 0,025
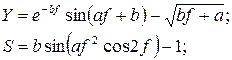 Вариант 4 a = -0,5
Вариант 4 a = -0,5
b = 10,7
f = 0,44
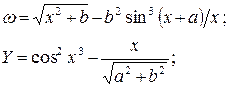 Вариант 5
Вариант 5
a = 1,5
b = 15,5
x = -2,9
Вариант 6
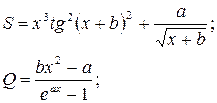 a = 16,5
a = 16,5
b = 3,4
x = 0,61
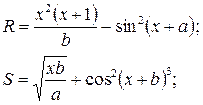 Вариант 7
Вариант 7
a = 0,7
b = 0,05
x = 0,5
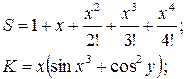 Вариант 8
Вариант 8
x = 0,335
у = 0,025
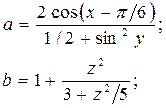 Вариант 9
Вариант 9
x = 1,582
у = -1,220
z = 2,9
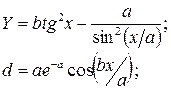 Вариант 10
Вариант 10
a = 3,2
b = 17,2
x = -4,8
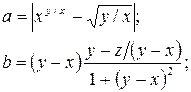 Вариант 11
Вариант 11
x = 2,152
у = 15,225
z = -2,322
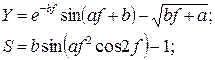 Вариант 12
Вариант 12
b = 15,5
f = -2,9
a = 1,5
Задание 2. Найти произведение и сумму 7 членов последовательности.
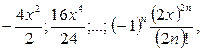 Вариант 1 x = 5
Вариант 1 x = 5
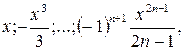 |
Вариант 2 x = 6
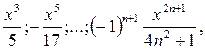 Вариант 3 x = 17
Вариант 3 x = 17
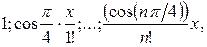 Вариант 4 x = 5
Вариант 4 x = 5
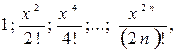 Вариант 5 x = 10
Вариант 5 x = 10
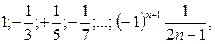 |
Вариант 6
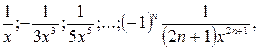 |
Вариант 7 x = 5
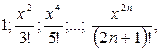 |
Вариант 8 x = 10
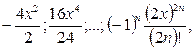 Вариант 9 x = 5
Вариант 9 x = 5
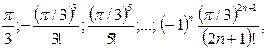 Вариант 10
Вариант 10
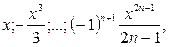 |
Вариант 11
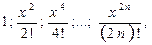 |
Вариант 12 х=6
Задание 3. Найти интегралы
| Вариант | ||
Формула интеграла
Формула интеграла
1
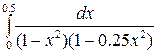
7
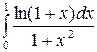
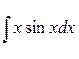
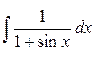
2
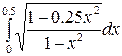
8
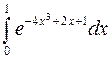
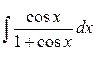
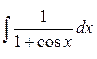
3
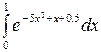
9
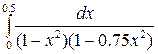
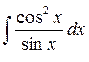
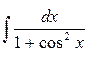
4
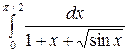
10
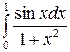
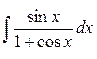
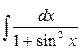
5
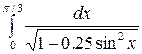
11
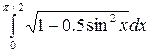
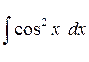
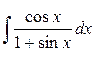
6
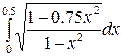
12
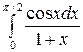
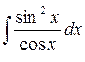
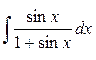
Задание 4. Найти производную функции
| Вариант | Функция | Вариант | Функция |
| 1 | 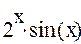
| 7 | 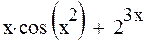
|
| 2 | 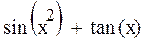
| 8 | 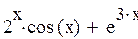
|
| 3 | 
| 9 | 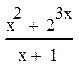
|
| 4 | 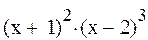
| 10 | 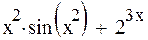
|
| 5 | 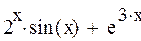
| 11 | 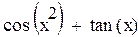
|
| 6 | 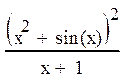
| 12 | 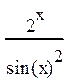
|
Задание 5. Для данной матрицы М
a) получить обратную матрицу М-1;
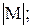 б) вычислить определитель
б) вычислить определитель
в) получить транспонированную матрицу МТ;
г) выделить элемент Мi,j;
д) выделить столбец М<i >
e) вычислите произведение 2*М
ж) вычислите произведение М*М.
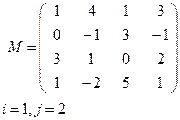 | 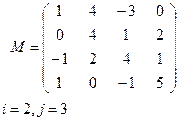 |
Вариант 1 Вариант 2
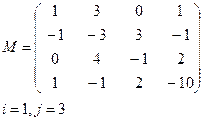 | 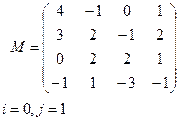 |
Вариант 3 Вариант 4
Вариант 5 Вариант 6
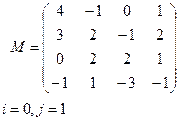 | 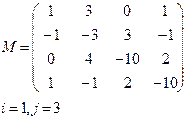 | ||
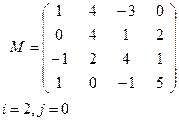 | 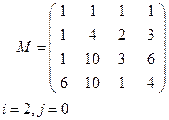 |
Вариант 7 Вариант 8
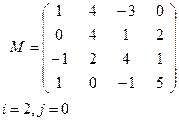 | 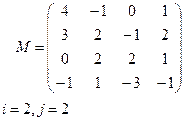 |
Вариант 9 Вариант 10
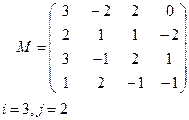 | 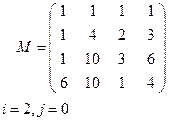 |
Вариант 11 Вариант 12
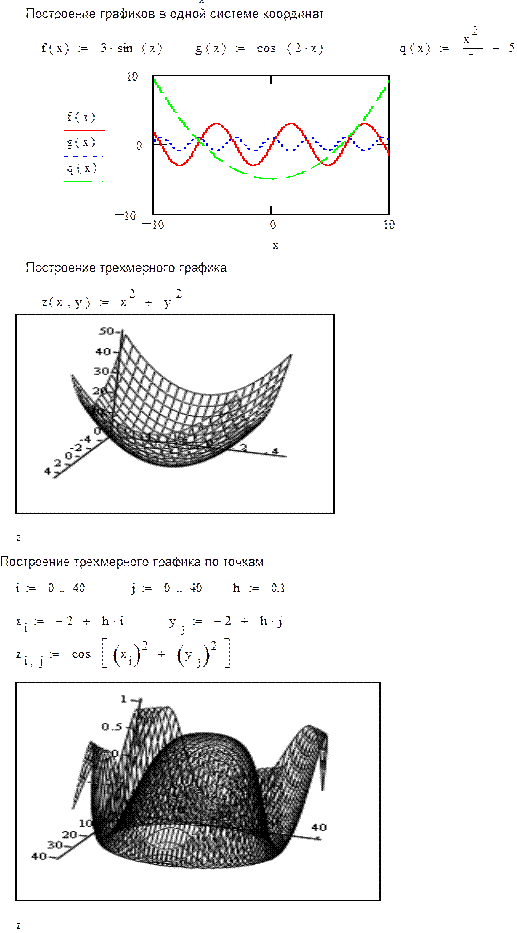
Построение графиков функций в MathCad. Решение задач линейного программирования с помощью MathCad
Чтобы построить двумерный график в координатных осях Х-У, надо дать команду Insert > Graph > X-Y Plot (Вставка > График > Декартовы координаты). В области размещения графика находятся заполнители для указания отображаемых выражений и диапазона изменения величин. Заполнитель у середины оси координат предназначен для переменной или выражения, отображаемого по этой оси. Обычно используют диапазон или вектор значений. Граничные значения по осям выбираются автоматически в соответствии с диапазоном изменения величины, но их можно задать и вручную.
В одной графической области можно построить несколько графиков. Для этого надо у соответствующей оси перечислить несколько выражений через запятую.
Разные кривые изображаются разным цветом, а для форматирования графика надо дважды щелкнуть на области графика. Для управления отображением построенных линий служит вкладка Traces (Линии) в открывшемся диалоговом окне. Текущий формат каждой линии приведен в списке, под которым расположены элементы управления, позволяющие изменять формат.
Для построения трехмерного графика необходимо задать матрицу значений. Отобразить ее можно в виде поверхности, столбчатой диаграммы или линий уровня. Примеры построения графиков приведены в приложении А.
Задание 1. Построить график функции и поменять вид кривой на зеленый пунктир.
| | 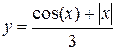
| | 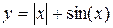
|
| | 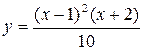
| | 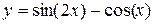
|
| | 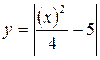
| | 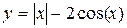
|
| | 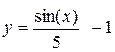
| | 
|
| | 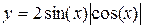
| | 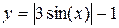
|
| | 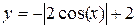
| | 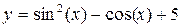
|
Порядок выполнения задания:
1. Введите функцию.
2. В панели математических знаков выбрать кнопку с изображением графика.
3. В палитре графиков щелкнуть на кнопке с изображением двумерного графика.
4. Ввести в место ввода шаблона по оси Х имя независимой переменной – х, а в место ввода шаблона по оси У имя зависимой переменной – у(х).
5. Нажать правую клавишу мыши на графике, выбрать меню Формат графика, во второй вкладке, появившегося окна изменить вид и цвет графика.
Построение графиков в Mathcad
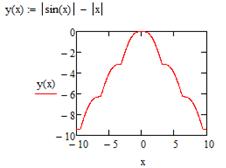
Задание 2. Построить график функции с условием на заданном интервале.
Порядок выполнения задания:
1. Для задания функции с условием используйте функцию if:
if(условие, выражение1если условие выполнено, выражение2 если условие не выполнено).
2. Для изменения интервала измените числа, стоящие в углах рамки графика по оси Х.
2. Для изменения интервала измените числа, стоящие в углах рамки графика по оси Х.
1. 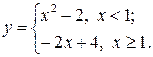
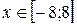
2. 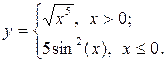
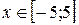
3. 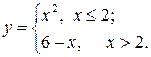
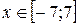
4. 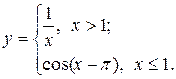
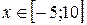
5. 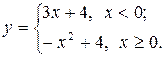
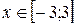
6. 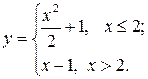
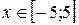
7. 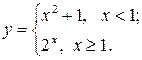
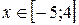
8. 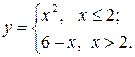
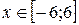
9. 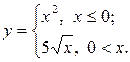
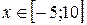
10. 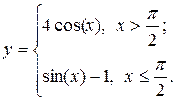
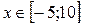
11. 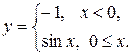
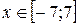
12. 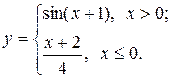
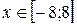
Задание 3. Построить графики функций из задания 1 и 2 в одной системе координат на интервале, указанном в задании 2.
Порядок выполнения задания:
1. Задайте данные функции (обозначьте их, например f(x) и g(x)):
2. Вызвав шаблон графика, введите по оси Х имя независимой переменной (или переменных, если их несколько),по оси Y введите f(x), поставьте запятую (при этом первое выражение уходит вверх, а под ним появляется место ввода), введите g(x).
3. Отведя указатель мыши за пределы графика, щелкните левой кнопкой мыши – появится график с двумя кривыми.
Задание 4. Построить трехмерный график (поверхность)
| 1. | 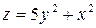
| 7. | 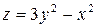
|
| 2. | 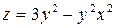
| 8. | 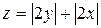
|
| 3. | 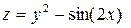
| 9. | 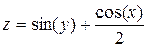
|
| 4. | 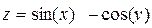
| 10. | 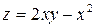
|
| 5. | 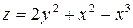
| 11. | 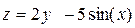
|
| 6. | 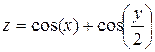
| 12. | 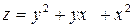
|
Задание 2.
Решить задачу линейного программирования в MathCad.
Для изготовления двух видов продукции А и В используются три вида сырья I, II, III. Ресурсы сырья, нормы его расхода на единицу продукции и получаемая прибыль от единицы продукции заданы в следующей таблице 4:
Таблица 2 – Расчетные данные
| Сырье | Нормы расхода | Ресурсы | |
| А | В | ||
| I | А1 | А2 | В1 |
| II | А3 | А4 | В2 |
| III | А5 | А6 | В3 |
| Прибыль | С1 | С2 | |
Определить оптимальный план выпуска продукции из условия максимизации прибыли.
Данные по вариантам берутся из таблицы 3.
Таблица 3 – Данные для таблицы 2
| № | A1 | A2 | A3 | A4 | A5 | A6 | B1 | B2 | B3 | C1 | C2 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 1 | 7 | 3 | 5 | 5 | 2 | 60 | 45 | 20 | 20 | 50 |
| 2 | 1 | 7 | 3 | 5 | 5 | 2 | 70 | 90 | 40 | 20 | 40 |
| 3 | 1 | 7 | 3 | 5 | 5 | 2 | 70 | 50 | 40 | 40 | 20 |
| 4 | 1 | 7 | 3 | 5 | 5 | 2 | 50 | 50 | 40 | 40 | 20 |
| 5 | 1 | 7 | 3 | 5 | 5 | 2 | 15 | 40 | 50 | 50 | 50 |
| 6 | 3 | 2 | 4 | 2 | 2 | 3 | 50 | 70 | 60 | 50 | 40 |
| 7 | 3 | 2 | 4 | 2 | 2 | 3 | 50 | 50 | 60 | 60 | 40 |
| 8 | 3 | 2 | 4 | 2 | 2 | 3 | 40 | 45 | 60 | 60 | 40 |
| 9 | 3 | 2 | 4 | 2 | 2 | 3 | 50 | 45 | 60 | 40 | 50 |
| 10 | 3 | 2 | 4 | 2 | 2 | 3 | 50 | 90 | 60 | 40 | 50 |
| 11 | 2 | 3 | 4 | 1 | 2 | 1 | 50 | 100 | 30 | 50 | 30 |
| 12 | 2 | 3 | 4 | 1 | 2 | 1 | 50 | 40 | 30 | 50 | 40 |
Метод средних
Рассмотрим еще один способ определения параметров эмпирической формулы – метод средних. Он состоит в том, что параметры a 1 , a 2 ,…, am зависимости (1) определяются с использованием условия равенства нулю суммы отклонений (2) во всех точках xi:

Полученное уравнение служит для определения параметров a 1 , a 2 ,…, am.
Метод наименьших квадратов
Запишем сумму квадратов отклонений для всех точек x 1 , x 2 ,…, xn:
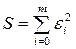 (3)
(3)
Параметры a 1 , a 2 ,…, am эмпирической формулы (1) будем находить из условия минимума функции S. В этом состоит метод наименьших квадратов. Минимум функции находим из условия равенства нулю частных производных по всем параметрам:
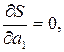
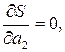 …
… 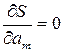 (4)
(4)
Полученные соотношения - система линейных уравнений для опреде-ления неизвестных параметров.
Для линейной функции y = ax + b эта система для определения коэффициентов a и b имеет вид:
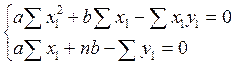 (5)
(5)
Решая эту систему уравнений, получаем:
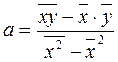
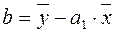 ,
,
где 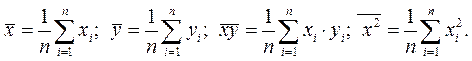
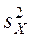 – значение дисперсии величины X, определяемой по формуле:
– значение дисперсии величины X, определяемой по формуле: 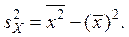
Коэффициент корреляции можно вычислить по формуле: 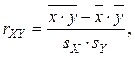
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции 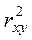 , называемый коэффициентом детерминации, он изменяется в пределах от 0 до 1.
, называемый коэффициентом детерминации, он изменяется в пределах от 0 до 1.
Чем выше показатель детерминации (>0,8), и чем ниже средняя ошибка аппроксимации Ā, тем лучше модель описывает исходные данные.
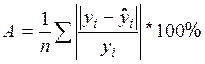
Линейная регрессия
Рассмотрим решение задачи обработки экспериментальных данных в Excel.
Пример 1. По семи областям региона известны данные за 200Xг. (табл. 1). Дана зависимость расходов на продукты в % к общим расходам (y) от среднемесячной заработной платы 1 работающего (тыс. руб., x).
Таблица 2 - Исходные данные
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| xi | 4,5 | 5,7 | 5,9 | 6,2 | 6,0 | 7,2 | 7,8 |
| yi | 68,8 | 62,6 | 58,3 | 54,5 | 57,1 | 52,1 | 51,0 |
Найти параметры уравнения линейной парной регрессии (различными способами) с помощью Excel и вычислить значение у при х=10.
Решение примера 1 в MS Excel с помощью инструмента анализа данных.
C помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительных интервалов, остатки и графики подбора линии регрессии. Если в меню Сервис еще нет команды Анализ данных, то необходимо сделать следующее. В главном меню последовательно выбираем Сервис→Надстройки и устанавливаем «флажок» в строке Пакет анализа.
Далее введите или скопируйте исходные данные.
Выбрать Сервис→Анализ данных→Регрессия. (или Данные - Анализ данных→Регрессия)
Заполните диалоговое окно ввода данных и параметров вывода (рис. 12).
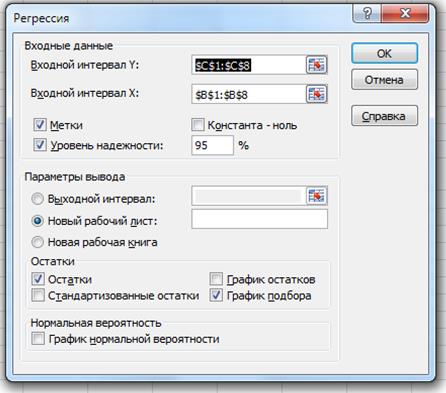
Рисунок 12 – Диалоговое окно
Здесь:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные признака-фактора;
Метки – «флажок», который указывает, содержи ли первая строка (в выделенных диапазонах) названия столбцов;
Константа – ноль – «флажок», указывающий на наличие или отсутствие свободного члена в уравнении (в нашем случае не ставить);
Уровень надежности – при включении этого параметра задается надежность 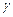 при построении доверительных интервалов.
при построении доверительных интервалов.
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Остатки – при включении вычисляется столбец, содержащий невязки 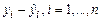 ;
;
Новый рабочий лист – можно указать произвольное имя нового листа (или не указывать, тогда результаты выводятся на вновь созданный лист).
Полученные результаты приведены в Приложении Б.
Видим, что коэффициенты, полученные с помощью табличных вычислений, не отличаются от рассчитанных с помощью Анализа данных и
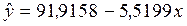
Используя эту формулу можно найти значение y при x=10. Получим y=36,7171, что совпадает с значением полученным с помощью встроенных функций в 1.1.
Пример 2. Построить линию тренда с помощью встроенных функций Excel.
Решение: Для построения уравнения регрессии необходимо выполнить следующие шаги:
- Введите и выделите столбцы с данными.
- Постройте по данным диаграмму выбрав тип точечный график.
- Выберите команду Добавить линию тренда в меню Диаграмма или в контекстном меню (сделав щелчок правой кнопкой).
- На вкладке Тип выберите нужный тип регрессионной линии тренда, во вкладке Параметры активизировать опции для вывода уравнения и величины достоверности аппроксимации (см. рис. 13).
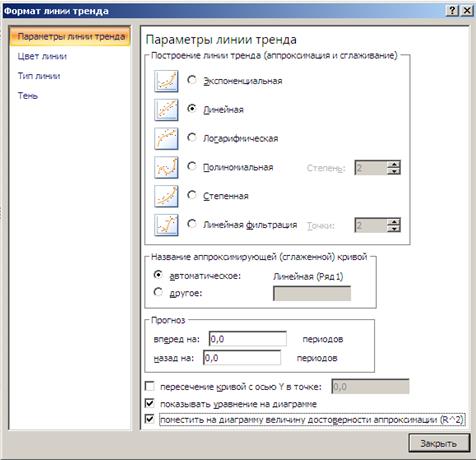
Рисунок 13 – Диалоговое окно параметров линии тренда
Для линейной аппроксимации получим следующий результат (рис. 14).
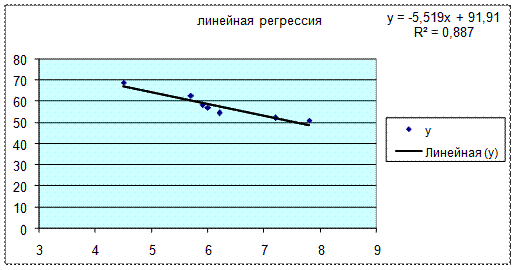
Рисунок 14 – Результат решения задачи
Задание 1. По предприятиям промышленности региона получена информация, характеризующая зависимость увеличения объема выпуска продукции (y, %.) от объема капиталовложений (x, млн. руб.).
Требуется:
Найти параметры уравнения линейной регрессии (различными способами).
Варианты 1,3,5,7,9,11


Варианты 2,4,6,8,10,12


ПРиложение Б
Данные для построения графиков
Вариант 1
| x | 0.1 | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 1.2 | 1.4 |
| y | 3.0 | 4.38 | 6.78 | 9.86 | 14.96 | 22.07 | 33.17 | 49.23 |
Вариант 2
| x | 0.05 | 0.2 | 0.4 | 0.6 | 0.9 | 1.2 | 1.5 | 1.8 |
| y | 0.521 | 1.555 | 3.572 | 5.622 | 7.801 | 11.77 | 14.78 | 17.82 |
Вариант 3
| x | 0.1 | 0.2 | 0.5 | 0.7 | 1 | 1.2 | 1.5 | 2.5 |
| y | 3.02 | 4.38 | 6.78 | 9.86 | 14.96 | 22.07 | 33.17 | 49.23 |
Вариант 4
| x | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | 2.0 | 3.0 | 4.0 |
| y | 11.213 | 8.0617 | 6.3512 | 4.8412 | 4.1201 | 0.9103 | 0.5413 | 0.1512 |
Вариант 5
| x | 0.1 | 0.5 | 1 | 1.7 | 2.50 | 3.5 | 5 | 6 |
| y | 109.13 | 40.271 | 14.728 | 5.5432 | 2.1201 | 0.8403 | 0.1733 | 0.2112 |
Вариант 6
| x | 0.2 | 0.45 | 0.6 | 0.8 | 1.0 | 3.0 | 5.0 | 7.0 |
| y | 4.455 | 9.034 | 9.952 | 11.38 | 12.52 | 17.98 | 20.55 | 22.23 |
Вариант 7
| x | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 2.0 | 4.0 | 6.0 |
| y | 6.733 | 4.027 | 1.762 | 1.452 | 1.211 | 0.693 | 0.423 | 0.312 |
Вариант 8
| x | 8.0 | 6.0 | 4.0 | 2.0 | 1.0 | 0.8 | 0.6 | 0.4 |
| y | 0.2813 | 0.6123 | 0.6512 | 1.6122 | 2.9201 | 3.8503 | 4.9123 | 7.6212 |
Вариант 9
| x | 0.05 | 2.0 | 4.0 | 6.0 | 8.0 | 10.0 | 12.0 | 14.0 |
| y | 0.0121 | 2.7312 | 4.1012 | 4.8112 | 5.7601 | 6.2203 | 7.0313 | 7.5812 |
Вариант 10
| x | 0.2 | 0.45 | 0.6 | 0.8 | 1.0 | 3.0 | 5.0 | 7.0 |
| y | 5.121 | 5.531 | 5.642 | 5.95 | 6.11 | 9.13 | 13.53 | 20.31 |
Вариант 11
| x | 0.2 | 0.4 | 0.6 | 0.8 | 1.0 | 3.0 | 5.0 | 7.0 |
| y | 17.23 | 19.11 | 19.52 | 20.03 | 20.52 | 22.67 | 23.73 | 24.55 |
Вариант 12
| x | 0.2 | 0.45 | 0.9 | 1.5 | 3.0 | 5.0 | 7.0 | 10 |
| y | -2.323 | -0.727 | -0.122 | 0.6582 | 0.9001 | 3.3103 | 4.1213 | 4.9812 |
Приложение B – Расчет параметров линейной парной регрессии с помощью пакета Анализа данных
| ВЫВОД ИТОГОВ |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| Регрессионная статистика |
|
|
|
|
|
|
| ||
| Множественный R | 0,9422 |
|
|
|
|
|
|
| |
| R-квадрат | 0,8876 |
|
|
|
|
|
|
| |
| Нормированный R-квадрат | 0,8652 |
|
|
|
|
|
|
| |
| Стандартная ошибка | 2,2950 |
|
|
|
|
|
|
| |
| Наблюдения | 7,0000 |
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| Дисперсионный анализ |
|
|
|
|
|
|
|
| |
| df | SS | MS | F | Значимость F |
|
|
| ||
| Регрессия | 1,0000 | 208,0598 | 208,0598 | 39,5034 | 0,0015 |
|
|
| |
| Остаток | 5,0000 | 26,3344 | 5,2669 |
|
|
|
|
| |
| Итого | 6,0000 | 234,3943 |
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
|
| Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | Нижние 95,0% | Верхние 95,0% | ||
| Y-пересечение | 91,9158 | 5,5013 | 16,7079 | 0,0000 | 77,7742 | 106,0574 | 77,7742 | 106,0574 | |
| x | -5,5199 | 0,8782 | -6,2852 | 0,0015 | -7,7775 | -3,2623 | -7,7775 | -3,2623 | |
|
|
|
|
|
|
|
|
|
| |
| ВЫВОД ОСТАТКА |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
| |
| Наблюдение | Предсказанное y | Остатки |
|
|
|
|
|
| |
| 1 | 67,0764 | 1,7236 |
|
|
|
|
|
| |
| 2 | 60,4525 | 2,1475 |
|
|
|
|
|
| |
| 3 | 59,3485 | -1,0485 |
|
|
|
|
|
| |
| 4 | 57,6926 | -3,1926 |
|
|
|
|
|
| |
| 5 | 58,7965 | -1,6965 |
|
|
|
|
|
| |
| 6 | 52,1727 | -0,0727 |
|
|
|
|
|
| |
| 7 | 48,8608 | 2,1392 |
|
|
|
|
|
| |
Аппроксимация функций
Орел 2018
ЛАБОРАТОРНАЯ РАБОТА № 1. Основы работы в системе MathCAD. Работа с матрицами. Построение графиков.
Документ программы MathCad называется рабочим листом. Он содержит объекты: формулы и текстовые блоки.В ходе расчетов формулы обрабатываются последовательно, слева направо и сверху вниз, а текстовые блоки игнорируются.
Ввод информации осуществляется в месте расположения курсора. Программа MathCad использует три вида курсоров. Если ни один объект не выбран, используется крестообразный курсор, определяющий место создания следующего объекта. При вводе формул используется уголковый курсор, указывающий текущий элемент выражения. При вводе данных в текстовый блок применяется текстовый курсор ввиде вертикальной черты.
Ввод формул
Формулы — основные объекты рабочего листа. Новый объект по умолчанию является формулой.
Элементы формул можно вводить с клавиатуры или с помощью специальных панелей управления. Панели управления (рисунок 1) открывают с помощью меню View (Вид) или кнопками панели управления Math (Математика). Для ввода элементов формул предназначены следующие панели:
° панель управления Arithmetic (Арифметика) для ввода чисел, знаков типичных математических операций и наиболее часто употребляемых стандартных функций;
° панель управления Evaluation (Оценка) для ввода операторов вычисления и знаков логических операций;
° панель управления Graph (График) для построения графиков;
° панель управления Matrix (Матрица) для ввода векторов и матриц и задания матричных операций;
° панель управления Calculus (Подсчет) для задания операций, относящихся к математическому анализу;
° панель управления Greek (Греческий) для ввода греческих букв (их можно также вводить с клавиатуры, если сразу после ввода соответствующего латинского символа нажимать сочетание клавиш CTRL+G, например [W][CTRL+G]-W);
° панель управления Symbolic (Символьный) для управления аналити-ческими преобразованиями.

Рисунок 1 - Панели инструментов программы MathCad
Чтобы начать ввод формулы, надо установить крестообразный курсор в нужное место и начать ввод букв, цифр, знаков операций. При этом создается область формулы, в которой появляется уголковый курсор, охватывающий текущий элемент формулы, например имя переменной (функции) или число. При вводе бинарного оператора по другую сторону знака операции автоматически появляется заполнитель в виде черного прямоугольника. В это место вводят очередной операнд.
Для управления порядком операций используют скобки, которые можно вводить вручную. Уголковый курсор позволяет автоматизировать такие действия. Чтобы выделить элементы формулы, которые в рамках операции должны рассматриваться как единое целое, используют клавишу ПРОБЕЛ. При каждом ее нажатии уголковый курсор «расширяется», охватывая элементы формулы.После ввода знака операции элементы в пределах уголкового курсора автоматически заключаются в скобки.
Например, для ввода формулы 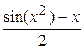 необходимо набрать
необходимо набрать 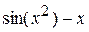
 затем нажать пробел и ввести
затем нажать пробел и ввести 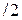 . Для ввода формулы
. Для ввода формулы 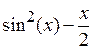 , записать
, записать 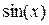 нажать пробел, чтобы уголковый курсор выделил всю формулу, возвести в степень, снова нажать пробел, а затем ввести
нажать пробел, чтобы уголковый курсор выделил всю формулу, возвести в степень, снова нажать пробел, а затем ввести 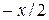 .
.
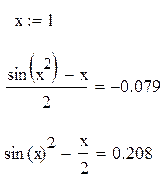
Введенное выражение обычно вычисляют или присваивают переменной. Для вывода результата выражения используют знак вычисления, который выглядит как знак равенства и вводится при помощи кнопки EvaluateExpression (Вычислить выражение) на панели инструментов Evaluation (Счет).
Знак присваивания изображается как «:=», а вводится при помощи кнопки AssignValue (Присвоить значение) на панели инструментов Evaluation (Счет). Слева от знака присваивания указывают имя переменной. Оно может содержать латинские и греческие буквы, цифры, символы «’», «_», а также описательный индекс. Последний вводится с помощью символа «.» и изображается как нижний индекс, но является частью имени переменной, например Vmin. Индексы, определяющие отдельный элемент вектора или матрицы, задаются по-другому, с помощью символа «[».
Переменную, которой присвоено значение, можно использовать далее в документе в вычисляемых выражениях. Чтобы узнать значение переменной, следует использовать оператор вычисления.
В следующем примере вычислена площадь круга с радиусом 2 (использованы переменные r и s, значение постоянной p определено в программе MathCad по умолчанию)

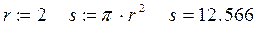
При изменении какой-либо формулы программа MathCad автоматически производит необходимые вычисления, обновляя изменившиеся значения и графики.
Ввод текста
Текст, помещенный в рабочий лист, содержит комментарии и описания и предназначен для ознакомления, а не для использования в расчетах. Текстовый блок создается нажатием кнопки с буквой А на панели инструментов или с помощью команды Insert>TextRegion (Вставка > Текстовый блок).
Иногда требуется встроить формулу внутрь текстового блока. Для этого служит команда Insert>MathRegion (Вставка > Формула).
Форматирование формул и текста
Для форматирования формул и текста в программе MathCad используется панель инструментов Formatting (Форматирование). С ее помощью можно индивидуально отформатировать любую формулу или текстовый блок, задав гарнитуру и размер шрифта, а также полужирное, курсивное или подчеркнутое начертание символов. В текстовых блоках можно также задавать тип выравнивания и применять маркированные и нумерованные списки.
В качестве средств автоматизации используются стили оформления. Выбрать стиль оформления текстового блока или элемента формулы можно из списка Style (на панели инструментов Formatting (Форматирование). Стиль оформленияимени переменной учитывается при ее определении. Так, переменные х и х рассматриваются как различные и не взаимозаменяемы.
Работа с матрицами
Векторы и матрицы рассматриваются в программе MathCad как одномерные и двумерные массивы данных. Число строк и столбцов матрицы задается в диалоговом окне InsertMatrix (Вставка матрицы), которое открывают командой Insert>Matrix (Вставка > Матрица). Вектор задается как матрица, имеющая один столбец.
После щелчка на кнопке ОК в формулу вставляется матрица, содержащая вместо элементов заполнители. Вместо каждого заполнителя надо вставить число, переменную или выражение.
При работе с матрицами приходится применять такие операции, как сложение матриц, умножение, транспонирование. Часто возникает необходимость в обращении матриц и в декомпозиции (разложении в произведение матриц специального вида). Программа MathCad позволяет выполнить все эти операции с помощью стандартных математических операторов (сложение, умножение) или встроенных функций.
Для работы с элементами матрицы используют индексы элементов. Нумерация строк и столбцов матрицы начинается с нуля. Для переопределения начала нумерации используют встроенную переменную ORIGIN. Индекс элемента задается числом, переменной или выражением и отображается как нижний индекс. Он вводится после щелчка на кнопке Subscript (Индекс) на панели инструментов Matrix (Матрица).
Пара индексов, определяющих элемент матрицы, разделяется запятой. Иногда (например, при построении графиков) требуется выделить вектор, представляющий собой столбец матрицы. Номер столбца матрицы отображается как верхний индекс, заключенный в угловые скобки, например М. Для его ввода используется кнопка MatrixColumn (Столбец) на панели инструментов Matrix (Матрица).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Чтобы задать общую формулу элементов матрицы, типа М i , j := i + j , используют диапазоны. Диапазон фактически представляет собой вектор, содержащий арифметическую прогрессию, определенную первым, вторым и последним элементами. Чтобы задать диапазон, следует указать значение первого элемента, через запятую значение второго и через две точки (используется кнопка 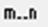 на панели Матрица) значение последнего элемента. Диапазон можно использовать как значение переменной, например x:=0,0.01..1.
на панели Матрица) значение последнего элемента. Диапазон можно использовать как значение переменной, например x:=0,0.01..1.
Если разность прогрессии равна единице (то есть элементы просто нумеруются), значение второго элемента и соответствующую запятую опускают. Например, чтобы сформировать по приведенной выше формуле матрицу размером 4х4, перед этой формулой надо указать i:=0..3 j:=0..3.
При формировании матрицы путем присвоения значений ее элементам размеры матрицы можно не задавать заранее. Всем неопределенным элементам автоматически присваиваются нулевые значения. Например, формула М3,3:= 1 создает матрицу М размером 4х4, у которой все элементы, кроме расположенного в правом нижнем углу, равны нулю.
Дата: 2018-12-28, просмотров: 343.
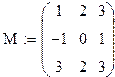
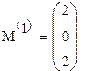
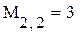
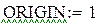
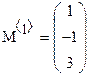
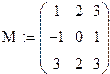
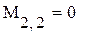
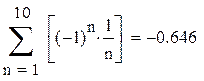
 Коэффициенты
Коэффициенты