Предположим, что в результате измерений в процессе экспериментов были получены n пар значений: ( x 1 , y 1 ), ( x 2 , y 2 ), …, ( x n , y n ). Задача состоит в том, чтобы найти приближенную зависимость y = f ( x ), значения которой при x = x i ( i =1,…, n ) мало отличаются от опытных данных yi.
Приближенная функциональная зависимость, полученная на основании экспериментальных данных, называется эмпирической формулой или уравнением регрессии.
Построение эмпирической формулы состоит из двух этапов: подбора общего вида этой формулы и определения наилучших значений содержащихся в ней параметров.
Общий вид формулы обычно выбирается из геометрических соображений: экспериментальные точки наносятся на график, и примерно угадывается общий вид зависимости путем сравнения полученной кривой с графиками известных функций (многочлена, показательной или логарифмической функции и т.п.).
Когда тип эмпирической формулы выбран, ее можно представить в виде:
y = f ( x , a 1 , a 2 ,…, am ). (1)
где f – известная функция, a 1 , a 2 ,…, am – неизвестные постоянные параметры, необходимо определить такие значения этих параметров, которые дают наилучшее приближение.
ОТКЛОНЕНИЕМ ei называется разность между значениями эмпирической функции (1) в точках x 1 ( i =1,…, n ) и опытными данными yi :
e i =f(xi,a1,a2,…,am)-yi . (2)
Задача нахождения наилучших значений параметров сводится к некоторой минимизации отклонений ei.
Существуют несколько методов решения этой задачи. Например, метод выбранных точек, метод средних, метод наименьших квадратов.
Метод выбранных точек
Он состоит в следующем: на примерном графике эмпирической функции выбираются точки, число которых равно количеству искомых параметров. Координаты этих точек тщательно измеряются для записи условия прохождения графика через выбранные точки. Из полученной таким образом системы уравнений находят значения параметров a 1 , a 2 ,…, am
Метод средних
Рассмотрим еще один способ определения параметров эмпирической формулы – метод средних. Он состоит в том, что параметры a 1 , a 2 ,…, am зависимости (1) определяются с использованием условия равенства нулю суммы отклонений (2) во всех точках xi:
Полученное уравнение служит для определения параметров a 1 , a 2 ,…, am.
Метод наименьших квадратов
Запишем сумму квадратов отклонений для всех точек x 1 , x 2 ,…, xn:
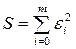(3)
Параметры a 1 , a 2 ,…, am эмпирической формулы (1) будем находить из условия минимума функции S. В этом состоит метод наименьших квадратов. Минимум функции находим из условия равенства нулю частных производных по всем параметрам:
… 
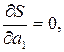
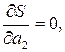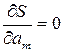(4)
Полученные соотношения - система линейных уравнений для опреде-ления неизвестных параметров.
Для линейной функции y = ax + b эта система для определения коэффициентов a и b имеет вид:
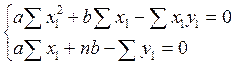(5)
Решая эту систему уравнений, получаем:
,
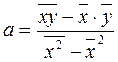
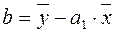где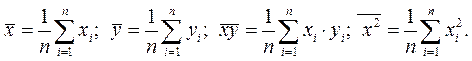 
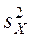– значение дисперсии величины X, определяемой по формуле: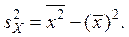 
Коэффициент корреляции можно вычислить по формуле: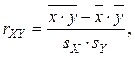 
Для оценки качества подбора линейной функции рассчитывается квадрат линейного коэффициента корреляции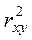 
, называемый коэффициентом детерминации, он изменяется в пределах от 0 до 1.
Чем выше показатель детерминации (>0,8), и чем ниже средняя ошибка аппроксимации Ā, тем лучше модель описывает исходные данные.
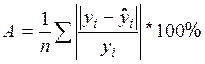
Линейная регрессия
Рассмотрим решение задачи обработки экспериментальных данных в Excel.
Пример 1. По семи областям региона известны данные за 200Xг. (табл. 1). Дана зависимость расходов на продукты в % к общим расходам (y) от среднемесячной заработной платы 1 работающего (тыс. руб., x).
Таблица 2 - Исходные данные
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| xi | 4,5 | 5,7 | 5,9 | 6,2 | 6,0 | 7,2 | 7,8 |
| yi | 68,8 | 62,6 | 58,3 | 54,5 | 57,1 | 52,1 | 51,0 |
Найти параметры уравнения линейной парной регрессии (различными способами) с помощью Excel и вычислить значение у при х=10.
Решение примера 1 в MS Excel с помощью инструмента анализа данных.
C помощью инструмента анализа данных Регрессия можно получить результаты регрессионной статистики, дисперсионного анализа, доверительных интервалов, остатки и графики подбора линии регрессии. Если в меню Сервис еще нет команды Анализ данных, то необходимо сделать следующее. В главном меню последовательно выбираем Сервис→Надстройки и устанавливаем «флажок» в строке Пакет анализа.
Далее введите или скопируйте исходные данные.
Выбрать Сервис→Анализ данных→Регрессия. (или Данные - Анализ данных→Регрессия)
Заполните диалоговое окно ввода данных и параметров вывода (рис. 12).
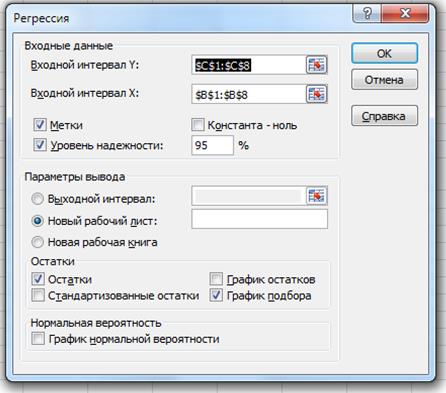
Рисунок 12 – Диалоговое окно
Здесь:
Входной интервал Y – диапазон, содержащий данные результативного признака;
Входной интервал X – диапазон, содержащий данные признака-фактора;
Метки – «флажок», который указывает, содержи ли первая строка (в выделенных диапазонах) названия столбцов;
Константа – ноль – «флажок», указывающий на наличие или отсутствие свободного члена в уравнении (в нашем случае не ставить);
Уровень надежности – при включении этого параметра задается надежность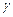 
при построении доверительных интервалов.
Выходной интервал – достаточно указать левую верхнюю ячейку будущего диапазона;
Остатки – при включении вычисляется столбец, содержащий невязки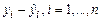 
;
Новый рабочий лист – можно указать произвольное имя нового листа (или не указывать, тогда результаты выводятся на вновь созданный лист).
Полученные результаты приведены в Приложении Б.
Видим, что коэффициенты, полученные с помощью табличных вычислений, не отличаются от рассчитанных с помощью Анализа данных и
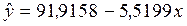
Используя эту формулу можно найти значение y при x=10. Получим y=36,7171, что совпадает с значением полученным с помощью встроенных функций в 1.1.
Пример 2. Построить линию тренда с помощью встроенных функций Excel.
Решение: Для построения уравнения регрессии необходимо выполнить следующие шаги:
- Введите и выделите столбцы с данными.
- Постройте по данным диаграмму выбрав тип точечный график.
- Выберите команду Добавить линию тренда в меню Диаграмма или в контекстном меню (сделав щелчок правой кнопкой).
- На вкладке Тип выберите нужный тип регрессионной линии тренда, во вкладке Параметры активизировать опции для вывода уравнения и величины достоверности аппроксимации (см. рис. 13).
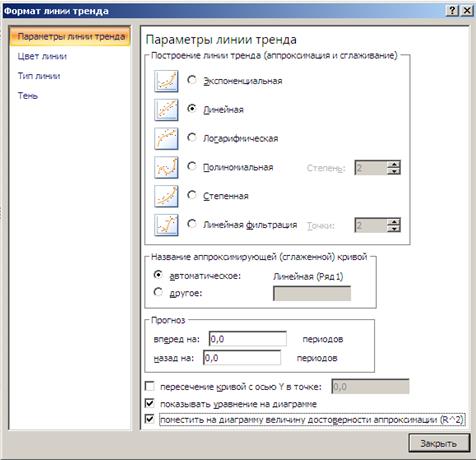
Рисунок 13 – Диалоговое окно параметров линии тренда
Для линейной аппроксимации получим следующий результат (рис. 14).
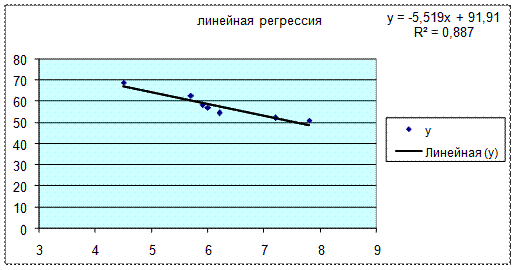
Рисунок 14 – Результат решения задачи
Задание 1. По предприятиям промышленности региона получена информация, характеризующая зависимость увеличения объема выпуска продукции (y, %.) от объема капиталовложений (x, млн. руб.).
Требуется:
Найти параметры уравнения линейной регрессии (различными способами).
Варианты 1,3,5,7,9,11
Варианты 2,4,6,8,10,12
Дата: 2018-12-28, просмотров: 241.
