Если многогранник рассечь плоскостью, то линия пересечения поверхности многогранника с плоскостью будет замкнутой плоской ломаной линией, т.е. многоугольником.
Каждая вершина этого многоугольника есть точка, в которой плоскость пересекла его ребро.
Каждая сторона этого многоугольника есть отрезок прямой линии, по которой плоскость пересекла грань многоугольника.
Для того чтобы построить линию пересечения плоскости с поверхностью многогранника необходимо:
1) Найти точки пересечения ребер многогранника с секущей плоскостью.
2) Соединить полученные точки отрезками. В результате этого получают стороны многоугольника, лежащего в плоскости пересекающей многогранник.
На рисунках 20 и 21 показаны примеры пересечения треугольной призмы и четырехугольной пирамиды плоскостями различного положения.
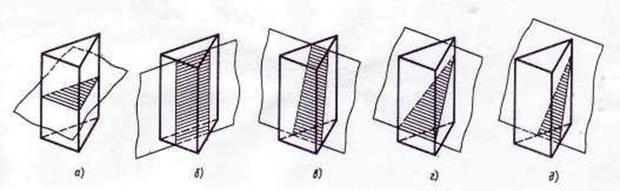
Рисунок 20
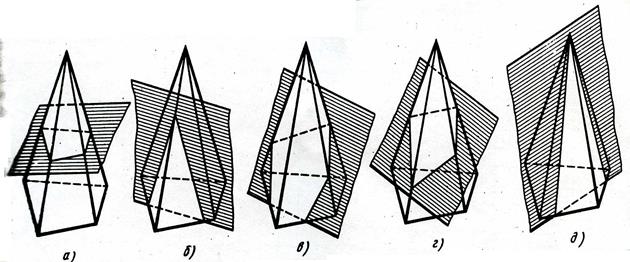
Рисунок 21
4.2 Контрольное задание №3
Построить комплексный чертеж усеченного тела.
В состав комплексного чертежа входят:
- ортогональные проекции;
- натуральная величина фигуры среза;
- развертка;
- прямоугольная изометрия.
4.2.1 Указания к решению контрольного задания
(Образец выполнения - рисунок 22)
1) Задание выполняется на формате А3;
2) Условия задачи даны в таблице 3;
3) В левой части формата строим 3 вида фигуры;
4) Призма пересечена фронтально-проецирующей плоскостью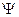 
;
5) Отсеченную часть призмы на проекциях и развертке изобразим тонкими линиями, а оставшуюся часть усеченной призмы обведем сплошной основной линией;
6) Т.к. плоскость 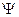перпендикулярна П2, она спроецируется на эту плоскость в прямую линию. На эту же линию спроецируется и фигура среза, лежащая в плоскости .
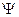7) Фигура среза на горизонтальной проекции совпадает с проекцией основания и изображается как правильный шестиугольник, т.к. линии среза принадлежат боковым граням призмы.
8) Используя линии проекционной связи, строим срез на П3.
9) Ни на одной из 3-х плоскостей проекций фигура среза не проецируется в натуральную величину, т.к. плоскость в которой она лежит, не параллельна ни одной из плоскостей проекций.
10) Строим натуральную величину фигуры среза методом вращения (рисунок 19) или методом перемены плоскостей проекций (рисунок 15).
11) Строим развертку усеченного тела:
- проводим прямую, на которой откладываем 6 отрезков, равных натуральной длине сторон основания (размеры берем с П1);
- из полученных точек проводят прямые, перпендикулярные данной прямой;
- на проведенных перпендикулярах, откладываем длины соответствующих усеченных ребер, измеренных на П2 или П3;
- полученные точки соединяют отрезками и получаем ломаную линию среза;
- вычерчиваем основание и натуральную величину среза.
12) Построение прямоугольной изометрической проекции:
- строим оси; они располагаются под углом 120º друг к другу;
- вычерчиваем основание шестиугольника в осях ХОУ (размеры берем с П1);
- из вершины проводим линии параллельные оси Z;
- на этих линиях откладываем длины усеченных ребер (измеряем их длину на П2 или П3);
- соединяем полученные точки и обводим фигуру с учетом видимости.
Таблица 3 - Исходные данные к контрольному заданию № 3
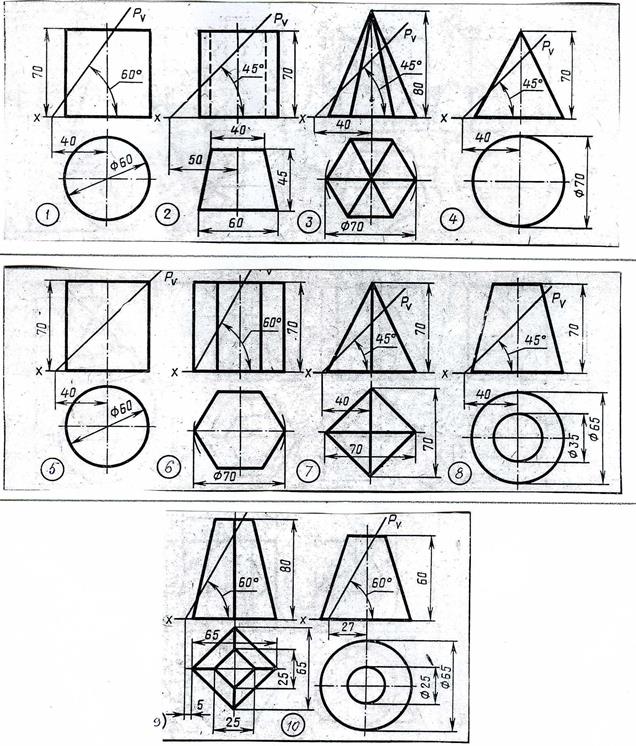
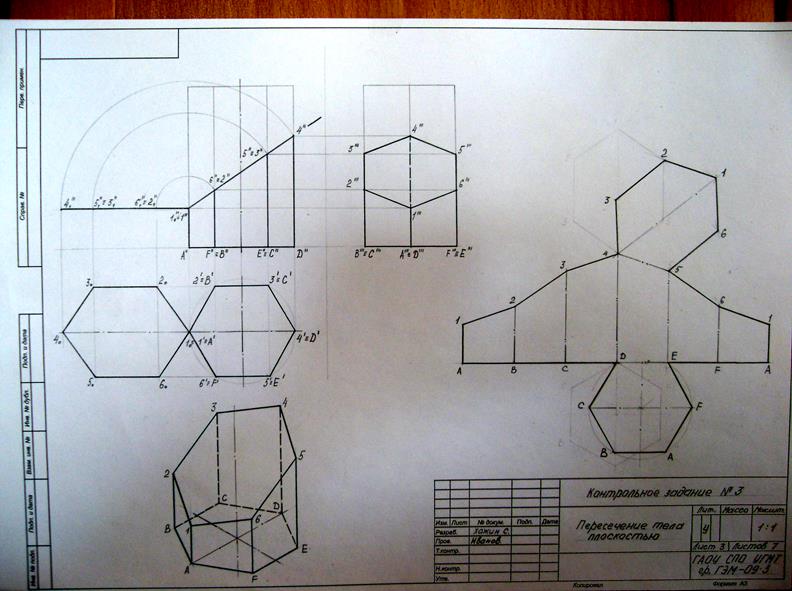
Рисунок 22
Пересечение поверхностей
При взаимном пересечении поверхностей образуются линии пересечения (линии перехода). Эти линии принадлежат одновременно 2-м поверхностям.
По форме они могут быть плоскими и пространственными кривыми ломаными линиями.
В зависимости от взаимного расположения поверхностей пересекающихся тел могут получиться:
- одна замкнутая линия взаимного пересечения, если поверхность одного геометрического тела частично прошла через поверхность второго геометрического тела (рисунок 23 а);
- две замкнутые линии, если поверхность одного геометрического тела полностью прошла через поверхность второго геометрического тела (рисунок 23 б).
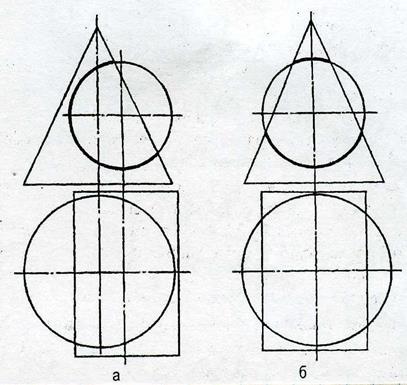
Рисунок 23
Начинать построение следует с характерных точек, расположенных на контурных линиях. Эти точки чаще всего определяют и границу видимости.
К характерным точкам относятся:
- самая верхняя и самая нижняя;
- левая и правая крайние точки.
Построить линию пересечения только по этим точкам нельзя. Необходимо ввести еще ряд промежуточных точек. Для их построения используют вспомогательные секущие плоскости.
Сущность метода заключается в том, что вводятся такие плоскости уровня, которые пересекают поверхности по графически простым линиям (окружностям, прямым). Эти линии, пересекаясь, дают точки, принадлежащие линии взаимного пересечения поверхностей .
5.1 Контрольное задание № 4
Построить 3 проекции пересекающихся тел и показать на них:
1) линию пересечения;
2) видимость линий пересечения и видимость очерков пересекающихся поверхностей и записать характерные точки линий пересечения.
5.1.1 Указания к решению контрольного задания
(Образец выполнения - рисунок 24).
1) Задание выполняется на формате А3 по условию, взятому из таблицы 4.
2) На рисунке 24 представлена задача на пересечение конической поверхности и сферы.
3) Строим три вида пересекающихся тел в тонких линиях.
4) На каждом из очерков пересекающихся поверхностей точки пересечения отыскиваются с помощью вспомогательных плоскостей, проведенных через каждый из контуров заданных поверхностей.
5) Прежде чем приступить к нахождению характерных точек, надо ответить на следующие вопросы:
a) Какие поверхности пересекаются? Если одна из них – проецирующий цилиндр, то одна из проекций линии пересечения совпадет с вырожденной проекцией цилиндра – окружностью.
b) Каково взаимное расположение поверхностей и следовательно, сколько пространственных кривых получится при их пресечении.
c) Имеется ли плоскость общей симметрии и каково её расположение в пространстве. Плоскость общей симметрии проходит через оси вращения пересекающихся поверхностей.
-если плоскость общей симметрии параллельной П2, то пересекутся фронтальные очерки поверхностей (рисунок 24, плоскость ω);
- если параллельная П1 – пересекутся горизонтальные очерки;
- параллельна П3 – профильные.
Поэтому без дополнительных проекций отмечаемся точки пересечения соответствующих очерков.
На рисунке 24, точки 1" и 2" отмечаем на пересечении фронтальных очерков, а затем строим их на П1 и П3. Точка 1 – самая верхняя; точка 2 – самая нижняя.
6) Горизонтальный контур сферы (экватор) пересекает конус в точках 3 и 31.
Чтобы построить их:
a) На П2 через экватор сферы вводим горизонтальную плоскость. Она рассечет:
- конус – по окружности;
- сферу - по окружности;
b) На П1 находим точки пересечения данных линий (3' и 31').
c) Строим их на П2 и П3.
7) Для нахождения точек, лежащих на профильном очерке конуса:
a) Вводим на П2 профильную плоскость τ. Она рассечет:
- конус – по треугольнику;
- сферу - по окружности.
b) На П3 находим точки пересечения данных линий (4"' и 41"'; 5"' и 51"'), а затем строим их на П2 и П1.
8) Промежуточные точки строим, используя плоскости уровня (точки 6 и 61 7 и 71).
9) В некоторых случаях характерные точки, лежащие на контуре одной из пересекающихся поверхностей, до определения промежуточных точек найти точно невозможно. Поэтому их отмечают приблизительно, после того, как кривая построена с учетом промежуточных точек. На рисунке 24 – это точки 8 и 81, лежащие на профильном контуре сферы. Порядок их нахождения:
- на П2 соединяем построенные точки и получаем проекцию кривой пересечения.
- отмечаем точки пересечения данной кривой с фронтальным очерком сферы и получаем точки 8" и 81", а затем строим их на П3 и П1.
10) Видимость линии пересечения на каждой из плоскостей проекций определяем по контуру тела, ближе расположенного к наблюдателю:
a) На П1 – видимость кривой решает та поверхность, горизонтальный контур которой выше;
b) На П2 – та поверхность, фронтальный контур которой ближе;
c) На П3 – профильный контур которой левее.
Поэтому кривая пересечения всегда меняет видимость на очерке ближней, по направлению взгляда поверхности.
На рисунке 24 кривая пересечения симметрична фронтальной плоскости ω, поэтому на П2 видимая часть – ближняя половина кривой пересечения (1",4",6",3",5",7", 8", 2") совпадает с невидимой частью (1",41",61",31",51",71", 81", 2").
На П1 видимой будет та часть линии, которая на П2 расположена выше экватора сферы (т.е. 3',6',4',1',41',61',31',). Точки 3' и 31' – границы видимости на П1.
На П3 видимой будет линия, которая расположена левее оси симметрии сферы на П1 (81''',2''', 8'''). Точки 8''' и 81''' – границы видимости на П3.
11) После определения видимости кривой пересечения необходимо определить видимость очерков сложной поверхности, образованной двумя пересекающимися телами.
a) На П2 фронтальные контуры сферы и конуса лежат в одной фронтальной плоскости ω, поэтому они видны до точек их пересечения 1'' и 2'', а в области наложения фронтальных проекций попадают внутрь поверхностей, т.е. не существуют и не обводятся (остаются в тонких линиях).
b) На П1 горизонтальный контур сферы (экватор); пересекает поверхность конуса в точках 3' и 31'. Он расположен выше горизонтального контура конуса и поэтому обводится от точки 31' влево до точки 3'. А горизонтальный очерк конуса в области наложения проекций не виден и обводится штриховой линией.
c) На П3 мы видим профильный очерк сферы расположенный выше точек 81''' и 8'''.
d) Очерк конуса сверху до точек 41''' и 4''' и снизу – до точек 51''' и 5''' виден только там, где он выходит из-за профильного очерка сферы, т.к. он расположен дальше от наблюдателя, чем сфера.
Образующие конуса от точек 41''' до 51''' и 4''' до 5''' попадают внутрь сферы и
поэтому не обводятся и остаются в тонких линиях (как несуществующие).
12) Записываем характерные точки линии пересечения:
- 1 и 2 – расположены на пересечении фронтальных очерков конуса и сферы;
- 1 – самая верхняя;
- 2 – самая нижняя;
- 3 и 31 - расположены на горизонтальном очерке сферы;
- 4 и 41; 5 и 51 – на профильном очерке конуса;
- 8 и 81 – на профильном очерке сферы.
Таблица 4 – Исходные данные к контрольному заданию № 4
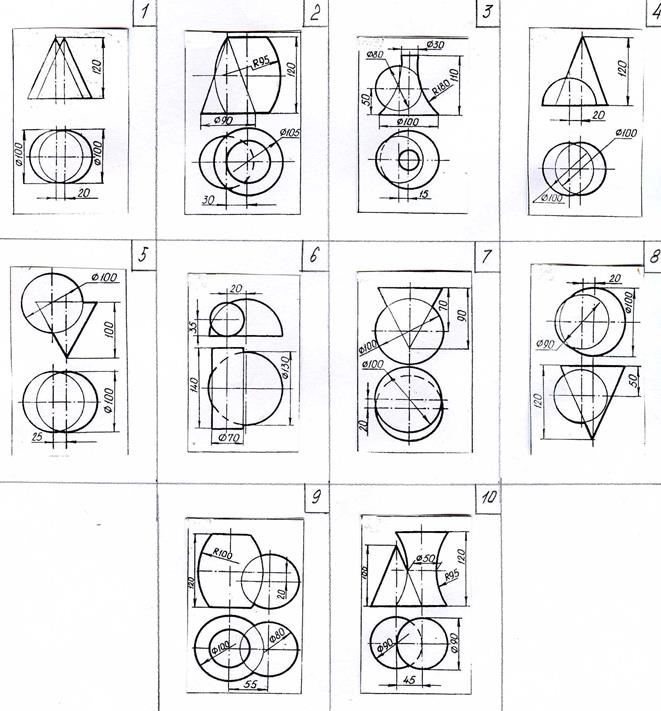
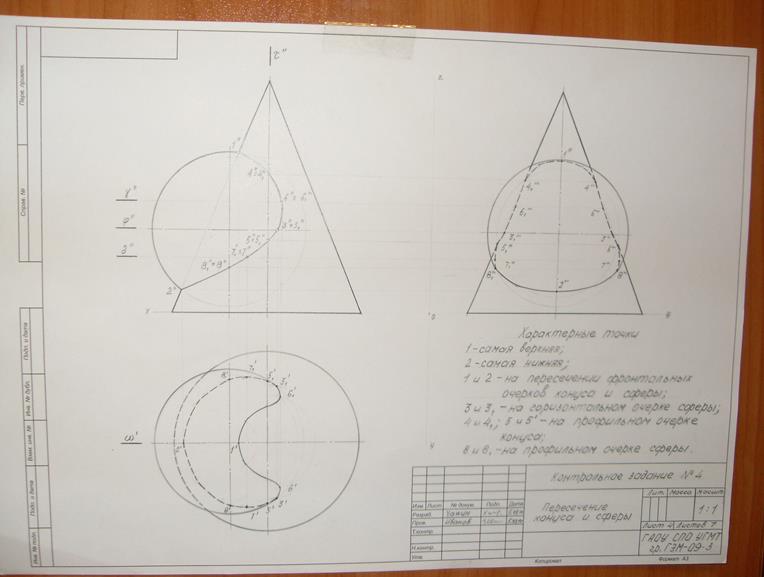
Рисунок 23
Дата: 2018-12-28, просмотров: 369.
